This set of Class 11 Physics Chapter 8 Multiple Choice Questions & Answers (MCQs) focuses on “Gravitation – Energy of an Orbiting Satellite”.
1. What is the magnitude of the ratio of KE and PE of a satellite revolving around a planet in a circular orbit of radius “R”?
a) 1:4
b) 1:2
c) 2:1
d) 3:2
View Answer
Explanation:Let the mass of the satellite be “m” and mass of the planet be “M”.
Kinetic energy (KE) = 1/2 x m x v2
= (1/2) x (G x m x M)/R
Potential energy (PE) = – (G x m x M)/R
KE : PE = -1:2
Therefore, (the magnitude of KE:PE) = 1:2.
2. What is the total energy possessed by a satellite of mass “m” orbiting above the earth of mass “M” and radius “R” at a height “h”?
a) [(G*M*m)/2*(R+h)]
b) -[(G*M*m)/2*(R+h)]
c) [(G*M*m)/(R+h)]
d) -[(G*M*m)/(R+h)]
View Answer
Explanation: Total energy (E) of a satellite is the sum of its potential energy (PE) and kinetic energy (KE).
PE = – (G x M x m)/(R+h)
KE = (G x M x m)/(2 x (R+h))
E = PE + KE
= -(G x M x m)/(R+h) + (G x M x m)/(2 x (R+h))
= -(G x M x m)/(2 x (R+h)).
3. A satellite of mass “m” is in a circular orbit of radius 1.5R around the earth of radius R. How much energy is required to move it to an orbit of radius 2R?
a) -(G*M*m)/12R
b) (G*M*m)/12R
c) -(G*M*m)/4R
d) (G*M*m)/4R
View Answer
Explanation: Total energy at 1.5R (TE) = -[(G*M*m)/3R] Total energy at 2R (TE’) = -[(G*M*m)/4R] The difference in energy is the required energy.
Difference = TE’ – TE
= -[(G*M*m)/4R] – [-[(G*M*m)/3R]] = -[(G*M*m)/4R] + (G*M*m)/3R] = (G*M*m)/12R.
4. A satellite revolves around the earth in a circular orbit with a velocity “v”. What is the total energy of the satellite? Let “m” be the mass of the satellite.
a) – (m*v2)/2
b) (m*v2)/2
c) (3*m*v2)/2
d) – (m*v2)
View Answer
Explanation: Total energy (E) = KE + PE
KE = (1/2) x m x v2
PE = – 2 x (KE) [For a satellite] = – m x v2
E = (1/2) x m x v2 + (- m x v2)
= – (1/2) x m x v2.
5. The figure shows the variation of energy with the orbital radius “r” of a satellite around a spherical planet.
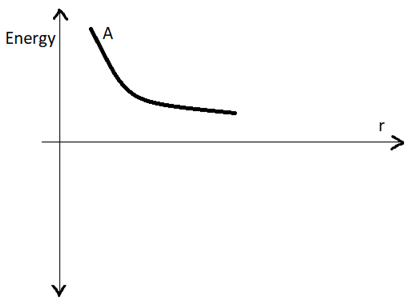
a) The curve A denotes the variation of kinetic energy with radius “r”
b) The curve A denotes the variation of potential energy with radius “r”
c) The curve A denotes the variation of total energy with radius “r”
d) The curve A denotes the variation of sum of potential energy and kinetic energy with radius “r”
View Answer
Explanation: The kinetic energy of a satellite is given by;
KE = (1/2) x (G x m x M)/r
Kinetic energy is inversely proportional to “r” and positive.
6. The figure shows the variation of energy with the orbital radius “r” of a satellite around a spherical planet.
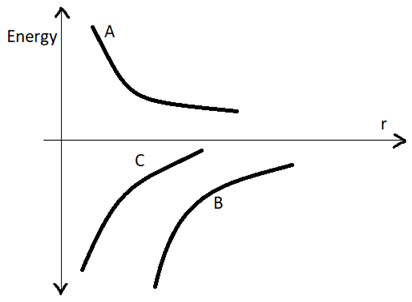
a) C shows the total energy, B the kinetic energy and A the potential energy
b) A shows the kinetic energy, B the total energy and C the potential energy
c) A shows the kinetic energy, B the potential energy and S the total energy
d) C shows the kinetic energy, A the potential energy and B the total energy
View Answer
Explanation: The kinetic energy of a satellite is given by;
KE = (1/2) x (G x m x M)/r
Kinetic energy is inversely proportional to “r” and positive. – Curve A
The potential energy is given by;
PE = – (G x m x M)/r
Potential energy is inversely proportional to “r” and negative. – Curve B
The total energy is given by;
TE = KE + PE
= (1/2) x (G x m x M)/r + – (G x m x M)/r
= – (1/2) x (G x m x M)/r.
Total energy is inversely proportional to “r” and negative. – Curve C
7. For a satellite with an elliptical orbit and not a circular orbit, the kinetic energy varies with time.
a) True
b) False
View Answer
Explanation: The kinetic energy of a satellite is;
KE = (1/2) x (G x m x M)/(R+h)
h: Height above the surface of the planet
For an elliptical orbit, “h” changes with time. Hence, the kinetic energy also varies with time.
8. For a satellite with an elliptical orbit and not a circular orbit, the potential energy varies with time.
a) True
b) False
View Answer
Explanation: The potential energy of a satellite is;
PE = – (G x m x M)/(R+h)
h: Height above the surface of the planet
For an elliptical orbit, “h” changes with time. Hence, the potential energy also varies with time.
9. Assume that a satellite executes perfectly circular orbits around a perfectly circular sphere. The work done by the satellite in 1 complete revolution is _____
a) (1/2) x (G x m x M)/(R+h)
b) – (G x m x M)/(R+h)
c) – (1/2) x (G x m x M)/(R+h)
d) 0
View Answer
Explanation: The net displacement of the satellite in one complete revolution is zero. Hence, the total work which is done by the satellite in one complete revolution also amounts to zero.
Work done = Force x Displacement.
10. If the kinetic energy of a satellite is halved, its orbital radius becomes _____
a) 1/2 times
b) 2 times
c) 4 times
d) infinity
View Answer
Explanation: The kinetic energy of a satellite is;
KE = (1/2) x (G x m x M)/r
r: Orbital radius
Let new kinetic energy be KE’
KE’ = KE/2
= [(1/2) x (G x m x M)/r]/2
= (1/2) x (G x m x M)/(2r)
= (1/2) x (G x m x M)/r’
r’: New orbital radius
r’ = 2r.
11. A satellite of mass “m” orbits a planet “P” in an elliptical orbit. The satellite is then transferred to another circular orbit of radius “r” as shown in the figure. Which of the following hold true in this scenario?
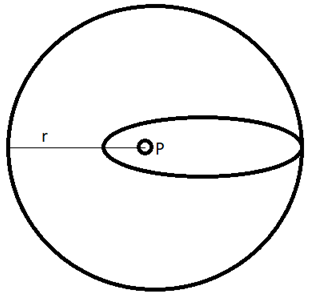
a) The kinetic energy of the satellite is increased and the potential energy of the satellite is decreased in the new orbit
b) The kinetic energy of the satellite is decreased and the potential energy of the satellite is increased in the new orbit
c) Both kinetic and potential energy of the satellite is decreased on the new orbit
d) Both kinetic and potential energy of the satellite is increased on the new orbit
View Answer
Explanation: The kinetic energy of a satellite is;
KE = (1/2) x (G x m x M)/r
The potential energy of a satellite is;
PE = – (G x m x M)/r
Due to an increase in “r” the kinetic energy is decreased. The potential energy increases for the same reason as well due to the presence of a negative sign.
12. For a satellite executing an elliptical orbit around a planet, its minimum potential energy is at the perigee.
a) True
b) False
View Answer
Explanation: Perigee is the point in the orbit closest to the surface of the planet. Hence, it has a maximum velocity. Therefore, at perigee, the kinetic energy is maximum and potential energy is minimum.
Sanfoundry Global Education & Learning Series – Physics – Class 11.
To practice all chapters and topics of class 11 Physics, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
- Check Class 11 - Physics Books
- Practice Class 11 - Mathematics MCQs
- Practice Class 11 - Chemistry MCQs
- Practice Class 12 - Physics MCQs
- Practice Class 11 - Biology MCQs
