This set of Class 11 Physics Chapter 15 Multiple Choice Questions & Answers (MCQs) focuses on “Displacement Relation in a Progressive Wave”.
1. What does the given equation: x = Asin(ky+wt+a) represent?
a) Wave travelling along positive x direction
b) Wave travelling along negative x direction
c) Wave travelling along positive y direction
d) Wave travelling along negative y direction
View Answer
Explanation: A way of looking at a travelling wave is considering the direction in which a particular value of transverse displacement moves. For the given equation x = Asin(ky+wt+a) we have to see the direction in which x moves. For eg: If we consider the amplitude A, for x =A as t increases, y should decrease. So, we can say that the wave propagates in the negative y direction.
2. An equation of a wave is given by: y = 2sin(3x-2t+π/2). What is the minimum distance between two points having the same phase?
a) 3
b) π/2
c) 2π/3
d) π
View Answer
Explanation: In the given equation the phase is 3x-2t+π/2.
This is repeated after every 2π.
∴ sin( 3x-2t+π/2) +2nπ = sin( 3x-2t+π/2).
We can consider the case at t=0, sin(3x+π/2) = sin(3x+π/2+2nπ)
OR cos(3x) = cos(3x+2nπ)
∴ n = 1 for minimum difference.
Minimum distance can be found from kx = 2π
OR x = 2π/k = 2π/3.
3. Consider a sinusoidal wave travelling in the positive x direction. What is the phase difference between the two points shown in the diagram below?
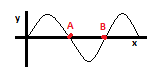
a) 0
b) π
c) π/2
d) 2π
View Answer
Explanation: Let the equation of the wave be y = Asin(kx-wt).
The x coordinate of the two points differs by λ/2.
So, the phase difference will be kλ/2 = (2π/λ)*(λ/2) = π.
An intuitive way to look at this is that both are at their mean positions right now and will be going in opposite directions at the next instant, so we can say they differ by π.
4. A sinusoidal wave has an amplitude of 2cm. It is travelling in the negative x-direction. The distance between two crests is 2cm. The angular frequency is πs-1. What is the displacement of the particle at x = 20.5cm, at t = 10s? Assume that at t=0 & x=0 the particle was at the mean position and going downwards. ‘x’ &’y’ are in cm.
a) 0cm
b) 1cm
c) -1cm
d) -2cm
View Answer
Explanation: The equation suiting the given conditions will be: y = Asin(kx+wt+a)
At x=0, t=0, velocity is negative, so ‘a’ will be π.
k = 2π/λ = π.
∴ y = 2sin(πx + 2t + π).
At x=20cm & t=10s,
y = 2sin(20.5π + 10π + π)
= 2sin(31.5π)
= -2cm.
5. The equation of a wave is given by y = 3sin(4x-2t). What is the time period and wavelength of the wave?
a) T = 2π, λ = 2π
b) T = π, λ = 2π
c) T = π, λ = π/2
d) T = π/2, λ = π
View Answer
Explanation: From the equation we get: k=4 & w=2.
Wavelength is given by 2π/k = 2π/4 = π/2.
Time period = 2π/w
= 2π/2 = π.
6. A sinusoidal wave has an amplitude of 3cm. Time period is 1s. The wavelength is 1cm. And at x = 0, t=0 the particle is at its mean position & moving upwards. What is the equation of the wave if it is travelling along the positive x-axis?
a) y = 3sin(2πx – 2πt)
b) y = 3sin(2πt – 2πx)
c) x = 3sin(2πt – 2πy)
d) y = 3cos(π + 2πt – 2πx)
View Answer
Explanation: The wave number k = 2π/1 = 2π.
The angular frequency w = 2π/1 = 2π.
The particle at x=0, t=0 is moving up from its mean position, & the wave travels towards the positive x-axis so the equation will be:
y = 3sin(2πt – 2πx).
Sanfoundry Global Education & Learning Series – Physics – Class 11.
To practice all chapters and topics of class 11 Physics, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
- Practice Class 11 - Biology MCQs
- Practice Class 11 - Chemistry MCQs
- Check Class 11 - Physics Books
- Practice Class 12 - Physics MCQs
- Practice Class 11 - Mathematics MCQs
