This set of Class 11 Physics Chapter 7 Multiple Choice Questions & Answers (MCQs) focuses on “Rolling Motion”.
1. A disc is under pure rolling motion on a horizontal surface. The speed of the topmost point at an instant is 5m/s w.r.t the centre of the disc. What is the velocity of the centremost point? The radius of the disc is 10cm.
a) 5m/s
b) 0m/s
c) 2.5m/s
d) 2m/s
View Answer
Explanation: The speed of any point w.r.t the centre is equal to R⍵,
where ‘ω’ is the angular speed & ‘R’ is the distance of that point from the centre.
In pure rolling motion, we know that V = Rω,
where V is the velocity of centre of mass.
∴ The velocity of centre of mass = 5m/s, since Rω = 5.
2. A disc is undergoing pure rolling motion on a flat surface. The radius of the disc is 5cm & velocity of centre of mass is 10m/s. What is the ratio of kinetic energy as seen from the ground frame to a frame moving along the disc with a speed of 10m/s?
a) 1:1, kinetic energy is frame independant
b) 3:1
c) 2:1
d) 1:3
View Answer
Explanation: The kinetic energy of a pure rolling disc as seen from the ground frame is given by: 1/2MV2 + 1/2Iw2.
I = MR2/2 w = V/R
∴ 1/2MV2 + 1/2Iw2 = 1/2MV2 + 1/4MV2 = 3/4MV2.
Kinetic energy as seen from the moving frame will only be the energy due to rotation about the disc’s axis.
∴ Kinetic energy from moving frame = 1/2Iw2 = 1/4MV2.
∴ Ratio = (3/4MV2) / (1/4MV2)
= 3:1.
3. What is the displacement of the centre of the wheel in one rotation? Let the radius of the wheel be R.
a) R
b) πR
c) 2πR
d) 0
View Answer
Explanation: Let the time taken for one rotation be ‘T’. Let the angular speed of the wheel be ‘w’. w = 2π/T.
The velocity of the centre is Rw = R*2π/T.
∴ Distance moved by it = R*2π/T*T
= 2πR.
4. A ring is at the top of the incline of angle and height ‘h’. If it is left from rest and goes down rolling purely, find its speed at the bottom.
a) √ (2gh) m/s
b) √ (gh/sinθ) m/s
c) √ (ghsinθ) m/s
d) √ (gh) m/s
View Answer
Explanation: Friction will be acting on the ring, which is the reason it is able to roll purely. But this friction will not do any work on the ring. The potential energy at the top will be converted into kinetic energy at the bottom. Kinetic energy is given by: 1/2MV2 + 1/2Iw2. I for a ring = MR2 & w = V/R.
∴ kinetic energy = 1/2MV2 + 1/2MV2 = MV2.
Potential energy at the top = Mgh.
Therefore, Mgh = MV2 OR V = √(gh) m/s.
5. A disc is purely rolling down an inclined plane of length ‘l’ & angle θ. What is the value of friction acting on it? Let the mass of the disc be M & radius be R.
a) (Mgsinθ)/3
b) 0
c) (4Mgsinθ)/3
d) (2Mgsinθ)/3
View Answer
Explanation: Let the angular acceleration of the disc be ‘α’. And the linear acceleration along the incline be ‘a’. For pure rolling, a = Rα. Mgsinθ – f = Ma———-(1), where f is the friction.
fR = Iα————–(2), where I is the moment of inertia = MR2/2.
fR = Ia/R, we substitute the value of a into the first equation,
Mgsinθ – f = (MfR2)/( MR2/2) = 2f
∴ Mgsinθ – f = 2f Or f = (Mgsinθ)/3.
6. In the diagram given below what is the direction of friction if the body is in pure rotational motion?

a) Up the incline
b) Down the incline
c) Zero
d) Depends on angle on inclination
View Answer
Explanation: For pure rolling the speed of centre at any instant should be the radius times its angular speed. While going down the incline speed is continuously increasing, so its linear & angular speed will be increasing. Friction will provide the necessary torque required for increasing angular speed. Thus, friction will act upwards so that its torque about the centre will cause the angular speed to increase in the clockwise direction.
7. The diagram given below shows a ring rolling purely on a flat surface, what is the ratio of velocity of points A to point B?
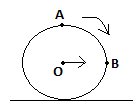
a) 1:2
b) 2:1
c) √2:1
d) 1:√2
View Answer
Explanation: The velocity of point A =vO+ R = 2R, since in pure rolling v0 = Rω.
Velocity of point B = √ (v02 + R2w2)
= √ (2R2w2)
=Rω√2.
Thus, ratio of velocities = 2Rω/Rω√2
= √2:1.
8. A ring, disc and solid sphere are left from the top of an incline which has sufficient friction for pure rolling. Which will reach the bottom first, if they all have the same mass ‘M’ & radius ‘R’?
a) Ring
b) Disc
c) Solid sphere
d) All will reach together
View Answer
Explanation: The equation of motions will be: Mgsinθ – f = Ma, where f is the friction & a is acceleration. Also, fR = Ia/R. From this equation ‘f’ will be substituted in the first equation: Mgsinθ – Ia/R2 = Ma.
∴ a = Mgsinθ / (I/R2+ M). Thus, more the value of I lesser will be the acceleration.
Moment of inertia of ring = MR2
Moment of inertia of disc= MR2/2
Moment of inertia of solid sphere = 2MR2/5
The solid sphere has the least moment of inertia, so it will have the maximum acceleration & hence it will take the least time. Note that if there was no friction their accelerations would be the same and they would reach together.
9. A sphere can roll purely on a smooth inclined surface. True or False?
a) True
b) False
View Answer
Explanation: For pure rolling, V = Rw at every instant of time, ( where V is the speed of the centre of the sphere & w is its angular speed). On an inclined surface a component of gravity is converting its potential energy to kinetic energy & thus ‘V’ is increasing, so ‘w’ should also increase. This requires presence of torque, which in this case is to be provided by friction. Hence, pure rolling on an incline requires the surface to be rough.
10. Which of the following options is correct for the given diagram? Let the friction coefficient be sufficient for pure rolling.
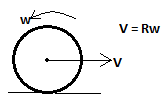
a) The sphere is in pure rolling motion
b) Friction force is zero
c) The motion is not pure rolling
d) Friction is acting in the direction of velocity of centre of sphere
View Answer
Explanation: For the motion to be pure rolling the velocity of contact point must be zero & V = Rw. From the frame of the centre of the sphere, the contact point has a speed of Rw in the forwards direction, so from the ground frame the velocity of contact point is V + Rw in the forwards direction. The sphere is slipping and thus, friction will act in the backward direction against the velocity of contact point.
11. What is the speed of a point of sphere in contact with the plank, if the sphere is in pure rolling motion in the given diagram? Consider the velocity of the plank to be positive.
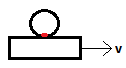
a) +v
b) -v
c) 0
d) -2v
View Answer
Explanation: There should be no slipping at the contact surface for pure rolling. Thus, the speed of the point of sphere in contact with the plank should also be v in the same direction.
12. The string holding the lift given below is cut. What will be the motion of the ring (as seen from inside the lift) initially at rest on top of the incline? The incline surface is rough.
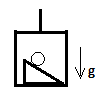
a) Pure rolling down the incline
b) Slide down the incline as normal will be zero due to free fall
c) Stay at its initial position
d) Fly upwards
View Answer
Explanation: When the string is cut, the entire system will be in free fall. The only force acting on the ring is in the vertically downward direction. When this is observed from inside the lift, even the observer is in free fall, so according to him the net force on the ring is zero and hence, it will stay at rest at its initial position. Note that for an observer on the ground the ring will be falling vertically downwards.
13. A disc is standing on a flat rough surface. Its centre is suddenly given a velocity of 5m/s in the forward direction. In how much time will pure rolling start? Mass = 1kg, Radius = 10cm. Coefficient of friction = 0.4.
a) 0.25 s
b) 0.05 s
c) 0.5 s
d) 1 s
View Answer
Explanation: Friction force will decrease its linear velocity & increase its angular velocity.
f = Ma . Friction ‘f’ = μN = 0.4*1*10 = 4N.
Thus, v = v0 – at & w = w0 + (a/R)t.
For pure rolling v = wR,
thus: v0 – at = R(w0 + (a/R)t). a = f/M ∴ 5 – 4/1 = 0.1(0 + (4/0.1)t)
∴ 10 = 40t
OR t = 0.25 s.
14. A solid sphere is given a horizontal velocity of 4m/s on a flat surface. What will be its velocity when it starts pure rolling? Mass = 2kg, Radius = 5cm. Coefficient of friction = 0.3.
a) It cannot roll purely
b) 2/3 s
c) 2s
d) 3s
View Answer
Explanation: Friction force ‘f’ will cause its speed to come down & increase its angular speed till V=Rw.
f = μN = 0.3*2*10 = 6N.
Thus, deceleration ‘a’ = 6/2 = 3m/s2.
And, angular acceleration = a/R = 3/0.05 = 60 rad/s2.
v = v0 – at = 4 – 3t.
w = w0 + (a/R)t = 0 + 60t = 60t.
At pure rolling, v=Rw
⇒ 4 – 3t = 0.05(60t)
∴ 4 = 3t + 3t = 6t.
∴ t = 2/3 s.
Sanfoundry Global Education & Learning Series – Physics – Class 11.
To practice all chapters and topics of class 11 Physics, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
- Check Class 11 - Physics Books
- Practice Class 11 - Chemistry MCQs
- Practice Class 11 - Biology MCQs
- Practice Class 12 - Physics MCQs
- Practice Class 11 - Mathematics MCQs
