This set of Class 11 Physics Chapter 7 Multiple Choice Questions & Answers (MCQs) focuses on “Dynamics of Rotational Motion about a Fixed Axis”.
1. A rigid body is rotating about an axis. One force F1 acts on the body such that its vector passes through the axis of rotation. Another force F2 acts on it such that it is perpendicular to the axis of rotation and at a point 5cm from the axis. This force F2 is perpendicular to the radius vector at its point of application. Find the net torque on the body. Let F1 = 10N & F2= 5N.
a) 0
b) 10.25Nm
c) 0.25Nm
d) 10Nm
View Answer
Explanation: The force F1 passes through the axis of rotation, so it will not produce a torque.
The force F2 is perpendicular to axis and radius, so it will provide a torque = r*F2 about the axis of rotation, where ‘r’ is the distance of point of application of force F2 from the axis of rotation.
Therefore, torque = r* F2= 0.05 * 5 Nm
= 0.25Nm.
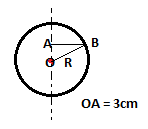
2. A ring is rotating about a diameter. The radius = 5cm & mass of ring = 1kg. A force is applied on the ring such that it is perpendicular to the axis and vector AB as shown in the figure. The magnitude of force is 10N. Find the work done by the torque, when the ring rotates by 90°.
a) 0.25π J
b) 0.15π J
c) 0.2π J
d) 0
View Answer
Explanation: Work done is given by Tθ, where T is the torque & θ is the angular displacement = π/2 rad. From the given figure, OA = 3cm & OB = 5cm,
therefore AB2 = 52 – 32= 25 – 9 = 16 OR AB = 4cm.
Torque due to force F will be AB*F = 0.04*10 = 0.4Nm.
∴ Work = Tθ = 0.4*π/2 = 0.2π J.
3. A ring of radius 7cm is rotating about the central axis perpendicular to its plane. A force acts on it, tangentially, such that it does a work of 10J in a complete rotation. Find the value of that force. `
a) 0.5/7π N
b) 35π N
c) 500/7π N
d) 0.7 N
View Answer
Explanation: Let the force be ‘F’. Work done will be = Tθ,
where T is the torque & is the angular displacement = 2π rad.
Work = Tθ = 10
∴ T(2π) = 10
∴ T = 5/π Nm.
Also, T = r*F
∴ 5/π = 0.07*F
∴ F = 500/7π N.
4. A disc of radius 10cm is rotating about the central axis perpendicular to its plane. A force of 5N acts on it tangentially. The disc was initially at rest. Calculate the value of power supplied by the force when the disc has rotated by 30°.The mass of the disc is 2kg.
a) 1.28W
b) 1.8W
c) 3.9W
d) 2.63W
View Answer
Explanation: Work done = Tθ, where T is torque & θ is angular displacement.
T = r*F = 0.1*5 = 0.5Nm
& θ = 30° = π/6 rad.
∴ Work = 0.5*π/6 = π/12 J.
Moment of inertia about spinning axis = MR2/2 = 2*0.01/2 = 0.01kgm2.
Using, T = Ia, where ‘I’ is moment of inertia & ‘a’ is angular acceleration, we get:
a = T/I
∴ a = 0.5/0.01 = 50 rad/s2.
Now, θ = w0t + (1/2)at2 to calculate the time for 30° rotation, where wo is initial angular velocity.
∴ π/6 = 0 + 0.5*50*t2.
∴ t = √(π/150) = 0.145 s.
∴ Power = Work/time = (π/12) / (0.145) = 1.8 W.
5. A rod is rotating about one end. If a force F1 acting on the other end produces a torque T & supplies power P, find the value of force F2 that will produce the same amount of power when it acts at the midpoint of the rod. Assume that all forces are perpendicular to the axis of rotation & axis of rod. The rod starts from rest.
a) = F1
b) > F1
c) < F1
d) No force acting at any other point will produce the same power
View Answer
Explanation: Power is defined as the work done per unit time. For the same power, the amount of rotation should be the same in a given time. For the th angular acceleration should be the same in both the cases & therefore the torque should be the same.
Thus, F2* I/2 = F1* I.
F2 = F1*2 OR F2 > F1
Sanfoundry Global Education & Learning Series – Physics – Class 11.
To practice all chapters and topics of class 11 Physics, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
- Practice Class 11 - Chemistry MCQs
- Practice Class 11 - Mathematics MCQs
- Practice Class 12 - Physics MCQs
- Practice Class 11 - Biology MCQs
- Check Class 11 - Physics Books
