This set of Class 11 Physics Chapter 7 Multiple Choice Questions & Answers (MCQs) focuses on “Linear Momentum of a System of Particles”.
1. Which of the following is the mathematical representation of law of conservation of total linear momentum?
a) dP/dt = 0
b) dF/dt = 0
c) dP/dt = Finternal
d) dF/dt = P
View Answer
Explanation: The law of conservation of linear momentum is derived from Newton’s second law. It states that total linear momentum is constant when external forces add up to zero. Newton’s second law: dP/dt = Fext. Here, Fext must be zero for conservation of linear momentum, thus dP/dt = 0.
2. A ball of mass 2kg is moving with a speed of 10m/s along a flat surface. It collides with another ball of mass 3kg and comes to rest, what will be the speed of the second ball after collision?
a) The above said situation is not possible
b) 20m/s
c) Zero
d) 6.67m/s
View Answer
Explanation: When the balls collide, net external force on them is zero, so we can conserve momentum. 2*10 = 3*v ∴ v = 20/3 = 6.67m/s.
Note that the final kinetic energy is less than the initial kinetic energy, this is because the internal forces have done work during collision which gets converted into sound & heat energy.
3. On collision of two balls linear momentum is conserved, it implies that even kinetic energy will remain conserved. True or False?
a) True
b) False
View Answer
Explanation: On collision of two balls, there is no external force, so the total momentum will be conserved. But due to internal forces there could be loss of energy in the form of heat, sound or deformation (potential energy) and hence final kinetic energy will be less than or equal to initial kinetic energy.
4. In the given figure, ball 1 has an initial velocity of 5m/s. Ball 2 is initially at rest. After collision ball 2 moves with a speed of 2m/s in the direction shown & ball 1 moves at an angle A. What is the value of angle A?
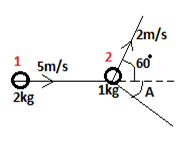
a) tan-1(1/3√3)
b) sin-1(1/3√3)
c) tan-1(1/√3)
d) tan-1(√3)
View Answer
Explanation: Linear momentum will be conserved since there is no external force.
Let the speed of ball 1 be v after collision.
We will conserve momentum in the horizontal and vertical direction separately.
2*5 = 1*2cos(60) + 2*vcos(A) & 1*2sin(60) = 2*vsin(A).
∴ 9 = 2vcos(A)———–(1) & √3 = 2vsin(A)—————-(2).
On dividing the 2 equations, we get:
tan(A) = 1 / 3√3.
5. A radioactive particle at rest, having mass 10g, breaks into 2 fragments (1&2) in the mass ratio 2:3 respectively. If the first one moves with a velocity of 10m/s what will be the speed of the second particle?
a) 4.33 m/s
b) -4.33 m/s
c) -6.67 m/s
d) 6.67 m/s
View Answer
Explanation: let the mass of part 1 be 2x, & the mass of part 2 be 3x since the masses are in the ratio 2:3. 2x + 3x = 10g.
∴ x = 2g. Therefore, masses of part 1 & 2 are 4g & 6g respectively.
The total momentum will be conserved because there is no external force. Let the velocity of 2nd part be ‘v’.
∴ 0 = 4*10 + 6*v ∴ v = -40/6 = -6.67 m/s.
6. There are two external forces acting on a system of particles. Select the correct statement.
a) Linear momentum is necessarily not conserved
b) Linear momentum may be conserved
c) Linear momentum is zero
d) Centre of mass will move with increasing speed
View Answer
Explanation: The two forces acting on the body may or may not have a net vector sum of zero, depending on which linear momentum may or may not be conserved. Thus, the option ‘linear momentum may be conserved’ is correct.
Sanfoundry Global Education & Learning Series – Physics – Class 11.
To practice all chapters and topics of class 11 Physics, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
- Practice Class 11 - Biology MCQs
- Practice Class 12 - Physics MCQs
- Check Class 11 - Physics Books
- Practice Class 11 - Mathematics MCQs
- Practice Class 11 - Chemistry MCQs
