Bernoulli's Equation - Class 11 Physics MCQ

This set of Class 11 Physics Chapter 10 Multiple Choice Questions & Answers (MCQs) focuses on “Fluids Mechanical Properties – Bernoulli’s Equation”.

1. Consider a tank of height 20m filled with liquid of density 100kg/m³. The area of tank is 10m². If the tank has a hole of area 2m² at the bottom, find the speed of the liquid flowing out through the hole when the height of liquid in the tank is 10m . Assume speed of liquid descending at top of tank is 5m/s.
a) 20m/s
b) 14.14m/s
c) 15m/s
d) 20.615m/s
View Answer

Answer: c
Explanation: We can’t consider the speed of efflux to be \(\sqrt{2gh}\) as the areas are comparable. So, we use Bernoulli theorem between the top of the tank and the hole. Pressure at the top of tank and hole will be same, equal to P₀, since both are exposed to the atmosphere.
P₀ + ρgH + 1/2ρ \(v_{1}^{2}\) = P₀+ 1/2ρ\(v_{2}^{2}\)
∴ v₂ = \(\sqrt{2(gh + v_{1}^{2}/2)}\)
= \(\sqrt{2(10 * 10 + 25/2)}\)
= 15m/s.

2. In which of the following conditions can the Bernoulli equation not be used?
a) Viscous flow
b) incompressible fluid
c) steady flow
d) laminar flow
View Answer

Answer: a
Explanation: Bernoulli’s equation can be used for non-viscous, incompressible and steady laminar flow.

3. The speed of efflux, in case of a tank with a hole at the bottom, depends upon which of the following factors? Assume that the area of the tank is > > area of hole.
a) area of tank
b) density of liquid
c) height of hole from liquid
d) atmospheric pressure value
View Answer

Answer: c
Explanation: Given that the area of the tank is > > area of hole, we can use the formula v = \(\sqrt{2gh}\). This shows that speed depends only on acceleration due to gravity and height of hole from the surface.

4. What will be the relation between H & L?

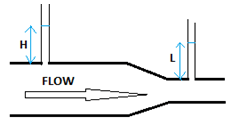
a) H = L
b) H > L
c) H < L
d) depends on the horizontal distance between the two tubes
View Answer

Answer: b
Explanation: By using Bernoulli’s equation P + ρgh + 1/2ρv² = constant,
we can say that more the velocity less is the pressure at the same horizontal level.
Height of liquid in the tube will be proportional to pressure at that point in the venturi tube.
So, H > L.

5. A cylindrical tank of Height H has a hole on its side. It is kept on a flat surface. Assuming that hole’s area is much smaller than the area of the tank, what should be the distance of the hole below the top surface so that water coming out of the hole travels the maximum horizontal distance at the instant when the height of water is H?
a) H
b) H/3
c) H/2
d) same for all positions
View Answer

Answer: c
Explanation: Let the hole be at a height x below the top surface.
The distance of hole from the ground will be H-x.
Speed of efflux ‘v’ = \(\sqrt{2gx}\).
Let the time taken for water to reach the ground be ’t’. H-x = 1/2gt².
∴ t = \(\sqrt{2/g(H – x)}\).
For maximum range, v*t should be maximum.
∴ d(\(\sqrt{2/g(H – x)}\)*\(\sqrt{2gx}\))/dx = 0
∴ d(\(\sqrt{Hx – x^2}\))/dx = 0
∴ (H-2x)/2 \(\sqrt{Hx – x^2}\) = 0
The numerator should be zero but denominator should be non-zero.
∴ H ≠ x (for denominator to be non-zero)
∴ H = 2x OR x = H/2.

Sanfoundry Certification Contest of the Month is Live. 100+ Subjects. Participate Now!

6. Water having density ‘⍴’ is flowing (steadily) downwards in the given tube. What is the relation between P_A & P_B?

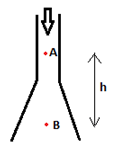
a) P_A = P_B
b) P_A < P_B
c) P_A > P_B
d) P_A – P_B= ⍴gh
View Answer

Answer: b
Explanation: The fluid speed will be less at B according to the equation of continuity (Av = const).
An intuitive way to think about this problem is that pressure at B has to be greater than that at A as the pressure difference not only has to balance gravity (which is trying to increase its velocity), but also decrease fluid speed. Another way is to use the Bernoulli equation.
P_A + ρgh + 1/2 ρv_A² = P_B + 1/2ρ v_B². A_Av_A = A_Bv_B
P_B – P_A = ρgh + 1/2 ρv_A² – 1/2 ρv_B²—————–(1)
v_B < v_A(because A_B > A_A)
Therefore we can say that R.H.S of equation (1) is positive
which in turn shows that P_B – P_A > 0.

7. Area 1 = 10m², Area 2 = 5m², rate of flow is 50m³/s. Find the value of H if the tubes contain mercury. Given that liquid flowing in the venturi tube is water.

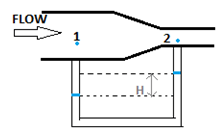
a) 28cm
b) 28m
c) 5.1cm
d) 5.1m
View Answer

Answer: a
Explanation: We can find the velocities from the given flow rate and areas at each point. A₁v₁ = A₂v₂ = 50. So, v₂ = 10m/s & v₁ = 5m/s.
P₁+1/2ρ\(v_1^2\) = P₂+1/2ρ\(v_2^2\) (where ρ is density of water flowing in venturi pipe)
P₁-P₂= 1/2ρ(\(v_2^2-v_1^2\))
∴ P₁ – P₂ = 1/2ρ(100-25) = 37.5ρ—————(1)
Now, for tubes containing mercury,
P₁ – P₂ = ρ₁gH ——————-(2) (where ⍴₁ is the density of mercury)
From (1) & (2) : ρ₁gH = 37.5ρ ⇒H = 37.5ρ / ρ₁₁ = 1/13.6 as the relative density of mercury is 13.6 times that of water).

8. Assume a ball is flying through air at rest. The speed of the centre of the ball is 5m/s (î). If the ball is spinning as shown below, find P_B – P_A. The ball has a radius (R) of 0.1m. Consider the speed of the ball to be constant as it passes through air. Let density of air be 1kg/m³. ω = 1(ĵ X î) rad/s.

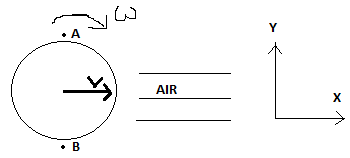
a) 0.2Pa
b) 2Pa
c) 0.1Pa
d) 1Pa
View Answer

Answer: d
Explanation: We can solve this question by sitting in the frame of the ball. The air will then move towards the ball from right to left. We should use the Bernoulli equation for two points A & B. P_A + ρg(2R) + 1/2ρ\(v_{A}^{2}\) = P_B + 1/2ρ\(v_{B}^{2}\) From the above equation we get P_B – P_A= ρg(2R) + 1/2ρ(\(v_{A}^{2} – v_{B}^{2}\)).
Now, from frame of the ball v_A = v – ⍵R = 5-0.1 = 4.9 &
V_B = v + ωR = 5 + 0.1 = 5.1
\(v_{A}^{2} – v_{B}^{2}\) = 4.9² – 5.1² = -2
∴ P_B – P_A= (1*10*0.2) – (0.5*1*2) = 2 -1 = 1.

9. A cylindrical tank, filled with water, has an area of 10m². A piston covers its entire top surface. A uniformly distributed load of 1000N is applied on the piston from top. A hole of area 0.001m²is at the bottom of the tank. Find the speed of efflux when the height of water level is 0.1m .
a) 24.5m/s
b) 1.48m/s
c) 0.2m/s
d) 2m/s
View Answer

Answer: b
Explanation: We should apply Bernoulli theorem between the top surface of water and the hole. The area of hole is very small when compared to the area of the tank. So, 1/2ρv² at the top surface of the tank can be neglected.
P₀ + F/AP + ρgh = P₀ + 1/2ρv²
∴ 1000/10 + 1000*10*0.1 = 0.5*1000 *v²
∴ v = 1.48m/s

10. A cylindrical tank of area 5m² contains water filled to a height of 10cm. A hole of area 0.005m² is present at the bottom. What is the time required for the water level to become half?
a) 100s
b) 10s
c) 1min
d) 10min
View Answer

Answer: a
Explanation: The speed of efflux when height of water is ’h’ = \(\sqrt{2gh}\). The volume of water flowing out in time dt is Avdt = 0.005*\(\sqrt{2gh}\)*dt. Therefore the decrease in height of water level (dh) in time dt is vol flowing out / area of tank = 0.005\(\sqrt{2gh}\)dt/5.
dh = \(\sqrt{2gh}\) (0.005)dt/5
\(\int_{0}^{0.05}dh/\sqrt{h} = \int_{0}^{t}\sqrt{2g}\)0.001 dt
∴ 2\(\sqrt{0.05}\) = \(\sqrt{20}\)0.001 t
∴ t = \(\sqrt{0.2}\)*1000/\(\sqrt{20}\) = 100s.

Sanfoundry Global Education & Learning Series – Physics – Class 11.

To practice all chapters and topics of class 11 Physics, here is complete set of 1000+ Multiple Choice Questions and Answers.

If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]

« Prev - Class 11 Physics MCQ – Fluids Mechanical Properties – Streamline Flow

» Next - Class 11 Physics MCQ – Fluids Mechanical Properties – Viscosity

Related Posts:

Recommended Articles: