Potential Energy of a System of Charges - Class 12 Physics MCQ

This set of Class 12 Physics Chapter 2 Multiple Choice Questions & Answers (MCQs) focuses on “Potential Energy of a System of Charges”.

1. The work done to move a charge of 20C by a distance of 2cm is 2J. What is the potential difference between those two points?
a) 1V
b) 0.1V
c) 10V
d) 20V
View Answer

Answer: b
Explanation: Work done to move a charge q in a potential difference of V is equal to q*V. According to the question, 2J=20C*Potential difference. Therefore, potential difference=\(\frac {2}{20}\)V=0.1V. The definition of 1J thus becomes, work done to move a charge of 1C from one point to another where the potential difference between the two points is 1V.

2.What should be the value of Q so that the potential energy of the system is zero?

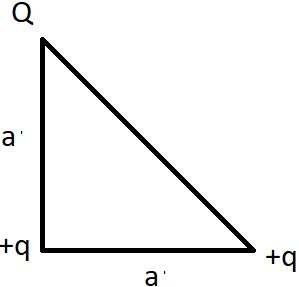
a) 2q
b) \(\frac {-q}{2}\)
c) √2 q
d) \(\frac {-2q}{(2 + \sqrt 2)}\)
View Answer

Answer: d
Explanation: The distance between the charges Q and +q is √2 a according to Pythagoras theorem. Therefore, the total potential energy of the system becomes (Q*\(\frac {q}{a}\)) + (q*\(\frac {q}{a}\)) + (Q*\(\frac {q}{\sqrt 2a}\)). But according to the question, the total potential energy is zero, i.e. (Q*\(\frac {q}{a}\)) + (q*\(\frac {q}{a}\)) + (Q*\(\frac {q}{\sqrt 2a}\)) = 0. Therefore, simplifying the equation, we get Q=\(\frac {-2q}{(2+\sqrt 2)}\).

3. +q charges are placed at a, 3a, 5a… (up to infinity) and –q charges are placed at 2a, 4a, 6a….. (up to infinity). What is the total potential energy at origin (0, 0)?
a) Zero
b) \(\frac {q}{a}\)
c) \(\frac {(q \, log2)}{a}\)
d) \(\frac {qe^2}{a}\)
View Answer

Answer: c
Explanation: The total potential energy at the origin due to the system is V=\(\frac {q}{a} – \frac {q}{2a} + \frac {q}{3a} – \frac {q}{4a} + \frac {q}{5a}\)……(up to infinity), where a, 2a, 3a… are the distances of the charges from the origin. Now, taking \(\frac {q}{a}\) common from the terms, we get V=\(\frac {q}{a} (1 – \frac {1}{2} + \frac {1}{3} – \frac {1}{4} + \frac {1}{5})\). By substituting the expansion of log2, we can get V=\(\frac {(q \, log2)}{a}\).

4. Four point charges 2*10^-9C, 1*10^-9C, -2*10^-9C, 3*10^-9C are placed at the corners of a square of side length √2m. What is the electric potential at the center of the square?
a) 36V
b) -36V
c) 2*10^-9V
d) Zero
View Answer

Answer: a
Explanation: Distance of the center of the square from the corner points=√2*\(\frac {\sqrt 2}{2}\)m=1m. Therefore, electric potential at the center of the square due to the charges = V=\(\frac {1}{4\pi \epsilon} \frac {(2*10-9+1*10-9-2*10-9+3*10-9)}{1}\)=9*10⁹*(2*10-9+1*10-9-2*10-9+3*10-9)=9*(2+1-2+3) =36V.

5. If three equal charges are placed at the corners of an equilateral triangle, the potential at the center of the triangle will be zero.
a) True
b) False
View Answer

Answer: b
Explanation: Electrostatic potential at a distance r from a point charge q is \(\frac {1}{4 \pi \epsilon} * \frac {q}{r}\). Therefore, adding this term three times, we get some positive value, not zero. Therefore, the potential energy at the center of the triangle is positive, not zero.

Note: Join free Sanfoundry classes at Telegram or Youtube

6. What is the potential energy at the center of an equilateral triangle if +5esu, +5esu and -10esu are placed at the corners of the triangle? The triangle has a side length of √3cm.
a) 20V
b) 5V
c) \(\frac {5}{3}\)V
d) 0V
View Answer

Answer: d
Explanation: Distance of the center of the triangle from every corner point is = \(\frac {2}{3} * \frac {\sqrt 3}{2}\) * √3cm=1cm [as we know that the center divides the median in a 2:1 ratio and the length of the median is \(\frac {2}{3}\)*side length]. Therefore, the potential at the center is =\(\frac {5}{1} + \frac {5}{1} -\frac {10}{1}\)=0 esu Volt.

7. +q charges are placed at the points (1, 0), (2, 0), (4, 0), (8, 0) …. (up to infinity). What is the potential at the origin due to these charges?
a) \(\frac {2q}{3}\)
b) 2q
c) \(\frac {q}{3}\)
d) Infinity
View Answer

Answer: b
Explanation: Electric potential due to the charges at the origin= q*\((\frac {1}{1} + \frac {1}{2} + \frac {1}{4} + \frac {1}{8} +…..=q*\frac {1}{1-\frac {1}{2}})\)=2q [by applying the formula of infinite G.P. series]. It can be shown that if the charges are alternately positive and negative, then the potential at the center would be \(\frac {2q}{3}\) .

Sanfoundry Global Education & Learning Series – Physics – Class 12.

To practice all chapters and topics of class 12 Physics, here is complete set of 1000+ Multiple Choice Questions and Answers.

If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]

« Prev - Class 12 Physics MCQ – Equipotential Surfaces

» Next - Class 12 Physics MCQ – Potential Energy in an External Field

Related Posts:

Recommended Articles: