This set of Class 11 Physics Chapter 7 Multiple Choice Questions & Answers (MCQs) focuses on “Vector Product of Two Vectors”.
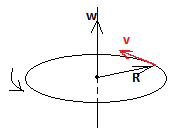
1. Regarding the velocity of a particle in uniform circular motion about a fixed axis, select the correct option. w & r angular velocity and radius vectors respectively. ‘X’ & ‘ . ’ represent cross & dot products respectively.
a) v = r X w
b) v = w X r
c) v = w.r
d) w = v.r
View Answer
Explanation: For a particle rotating about a fixed axis, its angular velocity vector points along the axis. Velocity of a particle is a vector so it will be a cross product and not a dot product. Now if we keep our fingers along the direction of the angular velocity vector and curl them in the direction of the radius we get the direction of velocity for that radius vector. Therefore, v = w X r. Refer to the diagram.
2. Which of the following statements is false?
a) Cross product is commutative
b) Cross product is distributive over addition
c) Dot product of two vectors gives a scalar
d) Dot product is commutative
View Answer
Explanation: Cross product a X b ≠ b X a, therefore it is not commutative. a X (b + c) = (a X b) + (a X c), therefore it is distributive over addition. Dot product is also known as scalar product & a.b = b.a, so it is commutative.
3. Find the vector product (a X b) of the two given vectors: a = 2i + 3j + 4k, b = 3i + 5j. Here, i, j & k are unit vectors along three mutually perpendicular axes.
a) -20i + 12j + k
b) 10i + 6j + 1/2k
c) 20i – 12j – k
d) 10i – 6j -1/2k
View Answer
Explanation: The cross product of a & b = i(0-20) – j(0 – 12) + k(10 – 9)
= -20i + 12j + k.
Note that this is not the same as b X a.
4. There are 6 vectors: a, b, c, d, e, f. Simply the following expression: [ a(b . c) X (e . f)d ] X [ a – d ].‘X’ represents cross product while ’.‘ represents dot product. Vectors a & d are perpendicular.
a) 0
b) (b . c)(e . f) [ d + a ]
c) (b . c)(e . f) [ d – a ]
d) (b . c)(e . f) [ d X a ]
View Answer
Explanation: [ a(b . c) X (e . f)d ] X [ a – d ]
= (b . c)(e . f) { [ a X d ] X [ a – d ] }
= (b . c)(e . f) { [ (a X d) X a ] – [ (a X d) X d ] }
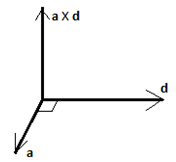
Now, (a X d) is perpendicular to the plane of a & d. Refer to the diagram below.
We see that (a X d) X a = d & (a X d) X d = −a.
Therefore, our expression = (b . c)(e . f) [ d + a ].
Sanfoundry Global Education & Learning Series – Physics – Class 11.
To practice all chapters and topics of class 11 Physics, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
- Check Class 11 - Physics Books
- Practice Class 11 - Mathematics MCQs
- Practice Class 11 - Biology MCQs
- Practice Class 12 - Physics MCQs
- Practice Class 11 - Chemistry MCQs
