This set of Class 11 Physics Chapter 14 Multiple Choice Questions & Answers (MCQs) focuses on “Simple Harmonic Motion”.
1. Which of the following variables has zero value at the extreme position in SHM?
a) Acceleration
b) Speed
c) Displacement
d) Angular frequency
View Answer
Explanation: At the extreme position in SHM, the body comes to instantaneous rest. The force, and therefore acceleration, is maximum at this point according to the force eqn: F = -kx.
2. A particle is initially at the centre and going towards the left. Let T be the time period of the SHM it is undergoing. What will be its position and velocity at time 3T/4, if it starts from the centre at t=0?
![]()
a) At right extreme, zero velocity
b) at centre, maximum speed towards left
c) at centre, maximum speed towards right
d) Mid-way between centre and -A
View Answer
Explanation: The time period of the given motion is T. It will go from centre to -A in T/4 secs. Then back to centre at 2T/4 secs. And then towards the right extreme, A, at 3T/4 secs. At this extreme position its velocity will be zero.
3. A particle is undergoing SHM with amplitude 10cm. The maximum speed it achieves is 1m/s. Find the time it takes to reach from the mean position to half the amplitude.
a) π/60 s
b) π/30 s
c) π/15 s
d) π/40 s
View Answer
Explanation: Let the equation of motion be: x = 0.1sin(wt) where w is the angular frequency.
On derivating this equation w.r.t time we get: v = 0.1wcos(wt).
Given that maximum speed is 1m/s, we get 0.1w = 1.
∴ w = 10s-1.
Now our equation of motion has become: x = 0.1sin(10t).
Assume we start from x=0 at t=0. Then by putting x=0.05 in the equation we can find the time. 0.05 = 0.1 sin(10t) ∴ sin(10t) = 0.5 ∴ 10t = π/6 ∴ t = π/60 s.
4. The displacement vs time graphs of 2 SHMs are given below. Which parameter is the same for both of them?
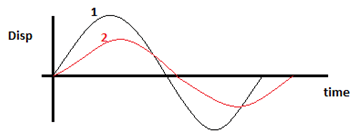
a) Angular frequency
b) Amplitude
c) Maximum speed
d) Phase constant
View Answer
Explanation: The time period is different for both as they both complete one cycle at different times. So, their angular frequencies will be different. The maximum displacement, as seen from the graph, is different for both so their amplitudes are different. SHMs have maximum speed at their mean positions. Both the curves have different slopes at their mean positions so their maximum velocities are different. At t=0, both are at their mean positions and going towards their positive extremes, therefore their phase constants will be the same.
5. 2 particles undergoing SHM start from the mean position and go in opposite directions. Particle 1 starts with a speed of 10m/s and particle 2 starts with a speed 0f 5m/s. If the amplitude(=10cm) is the same. At what position will they first meet?
a) 0.0866m
b) -0.0633m
c) 0
d) 0.0633m
View Answer
Explanation: Let the first particle go towards negative displacement. Its equation will be: x1 = 0.1sin(w1t + π) & maximum speed = 0.1w1=10
W1 = 100s-1.
Let the second particle go towards positive displacement. Its equation will be: x2 = 0.1sin(w2t) & maximum speed = 0.1w2 = 5
W2 = 50s-1.
Now, in their phasor diagram: w1t + w2t =2π.
∴ t = 2π/150.
At t = π/150
x1 = 0.1sin(50*2π/150) = 0.0866m.
6. A particle has an equation of motion given by: x = cos2wt – sin2wt. Select the correct statement regarding the same.
a) It is not a SHM
b) It is a SHM with T = π/w
c) It is an SHM with T = 2π/w
d) Amplitude of motion is 1/√2 m
View Answer
Explanation: x = cos2wt – sin2wt = cos 2wt.
Thus, time period T = 2π/2w = π/w.
Also the amplitude of motion is 1m.
7. What is the relation between time periods of the two given SHMs.
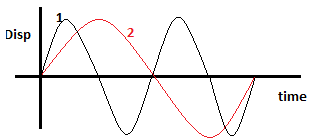
a) 4T1 = T2
b) T1 = 2T2
c) 2T1 = T2
d) T1 = 4T2
View Answer
Explanation: Particle 1 completes two cycles when 2 completes one cycle.
So, T1 = (1/2)T2
OR 2T1 = T2.
8. A particle starts from the extreme position, at t = 0, in a SHM. If the time period of motion is 2s & maximum speed is 5m/s, find the equation of motion.
a) x = 1.59cos(πt)
b) x = 1.59sin(πt)
c) x = 2.5sin(2t)
d) x = 2.5cos(2t)
View Answer
Explanation: T = 2s. ∴ w = 2π/T = s-1.
Aw = 5. ∴ A = 5/π metre.
x = 5/π sin(πt + a), where is phase constant.
At t = 0, x = A. Thus, a = π/2.
x = 5/π sin(πt + π/2)
= 5/π cos(πt) = 1.59cos(πt).
9. What is the amplitude of motion for x = 2sin(2t) + 4sin2t ?
a) 2√2 m
b) 4 m
c) 2 m
d) The given equation is not that of an SHM
View Answer
Explanation: x = 2sin(2t) + 4sin2t
= 2sin2t + 2(1-cos2t)
= 2sin2t – 2cos2t + 2
= 2√2 sin(2t – π/4) + 2.
Thus, the amplitude of motion is 2√2 m.
10. In an SHM the time taken to go from mean position to A/2 is the same as that from A/2 to A. True or False? Here, A is the amplitude of motion.
a) True
b) False
View Answer
Explanation: In a SHM, the speed is maximum at the mean position and goes on decreasing towards the extreme position. So the speed at every position from 0 to A/2 is greater than that from A/2 to A. Thus, the first half is covered faster.
11. In SHM, what is the phase difference between velocity and acceleration?
a) 0
b) π
c) π/2
d) π/3
View Answer
Explanation: Let the displacement of a particle be given by: x = Asin(wt).
Velocity will be = Awsin(wt + π/2)
acceleration will be = -Aw2sin(wt) = Aw2sin(wt + π).
Thus, the phase difference is π/2.
Sanfoundry Global Education & Learning Series – Physics – Class 11.
To practice all chapters and topics of class 11 Physics, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
- Practice Class 12 - Physics MCQs
- Practice Class 11 - Chemistry MCQs
- Check Class 11 - Physics Books
- Practice Class 11 - Biology MCQs
- Practice Class 11 - Mathematics MCQs
