This set of Class 11 Physics Chapter 8 Multiple Choice Questions & Answers (MCQs) focuses on “Gravitational Potential Energy”.
1. The force of gravity is a conservative force.
a) True
b) False
View Answer
Explanation: The amount of work done on the body by the force of gravity is independent of the path. Hence, it is a conservative force.
2. Conventionally, the magnitude of gravitational potential energy for an object at infinity from the earth is _____ ((M = Mass of the earth; m = Mass of the object at infinity; R = Radius of the earth).
a) -(G*M)/R2
b) -(G*M)/R
c) -(G*M*m)/R
d) Zero
View Answer
Explanation: Gravitational Potential Energy (U) = -(G*M*m)/r
At infinity, r -> infinity
Therefore, U -> 0.
3. The maximum value of gravitational potential energy is zero.
a) True
b) False
View Answer
Explanation: Since the reference for gravitational potential energy is taken at infinity, conventionally, we denote any finite value of gravitational potential energy, except zero, as a negative number. Hence, the greatest value of gravitational potential energy is zero.
4. A dam produces electricity from the gravitational potential energy of the water stored in it. The same dam has 50 cubic km of water stored 50 meters above the ground. What is the work done by gravity relative to the ground? (Assume g = 10 m/s2)
a) 1.5 x 1016 J
b) 2.5 x 1016 J
c) 3.5 x 1016 J
d) 4.5 x 1016 J
View Answer
Explanation: Mass of 50 cubic km of water = 5 x 1013 kg; Density of water = 1 g/cubic cm
Work done = m x g x h
= (5 x 1013 x 10 x 50) Joules
= 2.5 x 1016 J.
5. A 4kg eagle picks up a 75g snake and raises it 2.5 m from the ground to a branch. What is the work done by the eagle on the snake? (Assume g = 10 m/s2)
a) 100 J
b) 1.875 J
c) 118.75 J
d) 10 J
View Answer
Explanation: The work done by the eagle on the snake depends only on the mass of the snake.
Hence, the work done on the snake = (0.075 x 10 x 2.5) J
= 1.875 J.
6. A 4kg eagle picks up a 75g snake and raises it 2.5 m from the ground to a branch. What is the work done to raise the bird’s own centre of mass to the branch? (Assume g = 10 m/s2)
a) 100 J
b) 1.875 J
c) 118.75 J
d) 10 J
View Answer
Explanation: The work done to raise the bird’s own centre of mass to the branch depends only on the mass of the bird.
Hence, the work done = (4 x 10 x 2.5) J
= 100 J.
7. The expression for gravitational potential energy is “-(G*M)/r”.
a) True
b) False
View Answer
Explanation: The expression for gravitational potential energy is “-(G*M*m)/r”.
“-(G*M)/r” is the expression for ‘gravitational potential’.
Gravitational potential at a point can be defined as the work done in bringing a unit mass from infinity to that point.
8. Gravitational potential energy can be zero but gravitational potential can never be zero.
a) True
b) False
View Answer
Explanation: Gravitational potential at a point can be defined as the work done in bringing a unit mass from infinity to that point.Hence, for a given point mass at infinite distance, both, the gravitational potential and the gravitational potential energy can be zero.
9. Consider a ring of mass “M” as shown below. What is the gravitational potential at a point “p” at a distance of “r” from the centre of the ring?
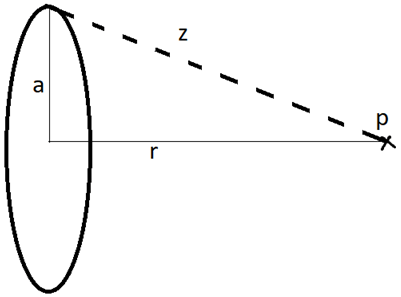
a) -(G*M)/(a2+r2) 1/2
b) -(G*M)/r1/2
c) -(G*M)/(a2+r2)2
d) -(G*M)/r2
View Answer
Explanation: Consider an element od mass “dm” of the ring at a distance “z” from the point “p”.
The gravitational potential (dV) due to this elemental mass at point “p” is;
dV = -(G*dm)/z
Integrating dV for the whole ring of mass “M”, we get;
V = -(G*M)/z
From Pythagorean theorem, we get;
z = (a2+r2) 1/2
Therefore; V = -(G*M)/(a2+r2)1/2.
10. The value of the gravitational potential at the centre of a ring of radius “a” and mass “M” is _____
a) zero
b) -(G*M)/a
c) -(G*M)/a1/2
d) infinite
View Answer
Explanation:We know that the gravitational potential at a point “p” at a distance of “r” from the centre of the ring of radius “a” and mass M” is;
V = -(G*M)/(a2+r2)1/2
At the centre of the ring; r = 0.
Therefore; V = -(G*M)/a.
11. The value of gravitational potential inside a uniform thin spherical shell is the same everywhere.
a) True
b) False
View Answer
Explanation: The gravitational potential inside a uniform thin spherical shell of radius “a” is;
V = -(G*M)/a, which is a constant. Hence, the value of gravitational potential inside a uniform thinspherical shell is the same everywhere and not necessarily non-zero.
12. The value of gravitational potential outside a uniform thin spherical shell is the same everywhere.
a) True
b) False
View Answer
Explanation: The gravitational potential outside a thin uniform spherical shell behaves similar to the potential due to a point source form the centre of the spherical shell.The gravitational potential outside a spherical shell is inversely proportional to the distance of the point outside from the centre of the sphere. Hence, it is not the same everywhere.
13. The gravitational potential energy of a body at a distance “r” from the centre of the earth is V. Its weight at a distance “2r” from the centre of the earth is _____
a) V/r
b) V/4r
c) V/2r
d) 4V/r
View Answer
Explanation: Gravitational potential energy (V) at a distance “r”;
V = -(G*M*m)/r
Gravitational force at a distance “r” = -(G*M*m)/r2
= V/r
Gravitational force at a distance “2r” = -(G*M*m)/4r2
= V/4r.
14. The velocity with which an object should be projected from the surface of the earth such that it reaches a maximum height equal to “n” time the radius of earth “R” is _____ (M = Mass of the earth)
a) [(n*G*M)/(n+1)R] 1/2
b) [((n+1)*G*M)/(n+1)R] 2
c) [(n*G*M)/(n+1)R]
d) [((n+1)*G*M)/nR] 2
View Answer
Explanation:Total initial energy = Total final energy
1/2(m x v2) – (G*M*m)/R = -(G*M*m)/(n+1)R
Simplifying the above equation, we get;
v = [(n*G*M)/(n+1)R]1/2.
15. The value ofthe gravitational field in a region is given by g = 2i + 3j. What is the change in gravitational potential energy of a particle of mass 5kg when it is taken from the origin O(0,0) to a point P(10, -5)? (Letters in bold are vectorial representations)
a) 5 J
b) 10 J
c) 25 J
d) 50 J
View Answer
Explanation: The gravitational potential energy, in vectorial mathematics, is the dot product of the gravitational field and relative position multiplied by mass.
Gravitational potential energy = (g . P) x m
= [(2i + 3j) .(10i – 5j)] x 5
= (20 – 15) x 5
= 25 J.
Sanfoundry Global Education & Learning Series – Physics – Class 11.
To practice all chapters and topics of class 11 Physics, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
- Practice Class 11 - Biology MCQs
- Practice Class 11 - Mathematics MCQs
- Practice Class 11 - Chemistry MCQs
- Practice Class 12 - Physics MCQs
- Check Class 11 - Physics Books
