This set of Class 11 Physics Chapter 3 Multiple Choice Questions & Answers (MCQs) focuses on “Straight Line Motion – Position, Path Length and Displacement”.
1. The displacement of a particle is given as function of time as x = t2 + 2t. How much displacement is covered in the first 5 seconds?
a) 5 units
b) 35 units
c) 40 units
d) 0 units
View Answer
Explanation: The displacement covered in the first five seconds can be obtained by putting t = 5 in the equation. Therefore, x = 55 + 2(5) = 25 + 10 = 35. Hence the answer is 35 units.
2. If, in the following diagram, distance between each circle is 1 unit, what is the displacement between A and B?
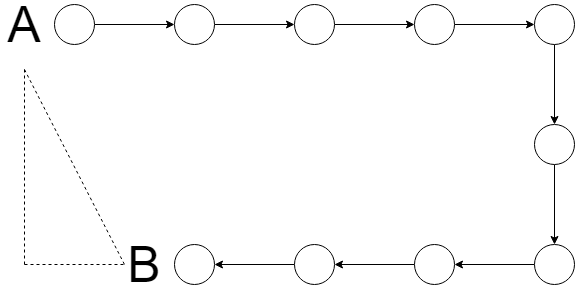
a) 5 units
b) Square root (5) units
c) 2 units
d) 1 unit
View Answer
Explanation: The vertical distance between A and B is of 2 units and the horizontal distance is 1 unit. Hence, to calculate the displacement, we can make a right-angled triangle as shown and can find the distance (AB) by Pythagoras theorem. Distance (AB) = Square root (22 + 12) = Square root (5).
3. Which one of the following relations is true?
a) Distance > Displacement
b) Distance < Displacement
c) Distance >= Displacement
d) Distance <= Displacement
View Answer
Explanation: Displacement is the shortest distance between two points. Hence displacement <= distance or vice versa. If the path followed is the path of shortest distance or displacement, then displacement = distance.
4. A person is standing at -2 location on the number line. He runs to and fro from -2 to +5 location 5 times. How much distance has he covered if he comes back to -2 location at the end?
a) 35 units
b) 7 units
c) 30 units
d) 15 units
View Answer
Explanation: In one turn the person covers 5 – (-2) units of distance, i.e. 7. Therefore in 5 turns, he will cover 5 x 7 = 35 units of distance.
5. What is the path length of the following path?
A (0, 0) to B (5, 0) to C (5, 5) to D (0, 5)
a) 20 units
b) 25 units
c) 15 units
d) 10 units
View Answer
Explanation: Total path length = Sum of path lengths of intermediate paths. Therefore, Path length AD = Sum of Path lengths of AB, BC, CD = 5 + 5 + 5 = 15 units.
6. When person moves in the coordinate system from A (0, 0) to B (5, 10), to C (8, 6), what is the displacement covered?
a) 10 units
b) 5 units
c) 7 units
d) 15 units
View Answer
Explanation: The displacement is the distance between the final and the initial location. Here the final location is C and the initial is A. We can solve this by using distance between two points method. AC = Square root ((82 – 02) + (62 – 02)) = Square root (100) = 10 units.
7. Displacement between two points is ___
a) The shortest path
b) The longest path
c) Equal to distance
d) Greater than distance
View Answer
Explanation: Displacement between two points is the shortest path between them. It is always less than or equal to the distance between them. Displacement can never be greater than distance.
8. Distance does not depend on _______
a) Initial point
b) Final point
c) Path taken
d) Speed
View Answer
Explanation: The distance depends on the final and initial points as these points define the path. Distance also depends on the path chosen, the distance between same initial and final point with different paths can be different. It does not depend on speed as whatever the speed may be, if the initial and final points and path remains same, the distance remains same.
9. How many variables are required to define the position of a body in space?
a) 3
b) 2
c) 1
d) 0
View Answer
Explanation: In space we require a minimum of 3 variables to describe the position of a body, namely x, y, and z (in Cartesian system). There are also systems other than Cartesian Coordinate system to do this like Cylindrical system, Spherical or Radial system.
10. In which coordinate system do we use distance from origin and to angles to define the position of a point in space?
a) Cartesian
b) Cylindrical
c) Spherical
d) 2-D Cartesian
View Answer
Explanation: In Spherical system, distance from the center, the angle with the X axis, and the angle with the Z axis are used to define the position of a point. These are respectively represented by R, θ and ф.
11. Which of the following is the correct formula for finding distance (d) between two points (x1, y1) and (x2, y2)?
a) d2 = (x2-x1)2 + (y2-y1)2
b) d4 = (x2-x1)2 + (y2-y1)2
c) d3 = (x2-x1)2 + (y2-y1)2
d) d = (x2-x1)2 + (y2-y1) 2
View Answer
Explanation: The correct answer is d2 = (x2-x1)2 + (y2-y1)2. This expression can be found out using Pythagoras theorem in Cartesian coordinate system. Build a right-angle triangle with sides parallel to the axes and the hypotenuse joining the two points to construct the right-angle triangle.
12. Path length does not depend on ____
a) Initial point
b) Final point
c) Path taken
d) Coordinate system
View Answer
Explanation: The path length depends on the final and initial point. It also depends on the path taken. But it does not depend on the coordinate system. The coordinate system merely defines thee path and does not affect its total length.
Sanfoundry Global Education & Learning Series – Physics – Class 11.
To practice all chapters and topics of class 11 Physics, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
- Practice Class 11 - Mathematics MCQs
- Check Class 11 - Physics Books
- Practice Class 12 - Physics MCQs
- Practice Class 11 - Biology MCQs
- Practice Class 11 - Chemistry MCQs
