This set of Class 11 Physics Chapter 7 Multiple Choice Questions & Answers (MCQs) focuses on “System of Particles and Rotational Motion”. These MCQs are created based on the latest CBSE syllabus and the NCERT curriculum, offering valuable assistance for exam preparation.
1. The centre of masses of two particles with masses 2 kg and 1 kg located at (1,0,1) and (2,2,0) is located at _____
a) 4/3, 2/3, 2/3
b) 2/3, 4/3, 2/3
c) 2/3, 2/3, 4/3
d) 1/3, 2/3, 2/3
View Answer
Explanation:Sum of masses = 2+1 = 3
x-coordinate;
(2*1 + 1*2)/3 = 4/3
y-coordinate;
(2*0 + 1*2)/3 = 2/3
z-coordinate;
(2*1 + 1*0)/3 = 2/3.
2. Two bodies of masses 5kg and 15kg are located in the cartesian plane at (1,0) and (0,1). What is the location of their centre of mass?
a) 1/4, 1/4
b) 3/4, 3/4
c) 3/4, 1/4
d) 1/4, 3/4
View Answer
Explanation: Sum of masses = 5 + 15 = 20
x-coordinate;
(5*1 + 15*0)/20 = 1/4
y-coordinate;
(5*0 + 15*1)/20 = 3/4.
3. The coordinates of the centre of mass of objects of mass 10, 20, 30 kg are (1,1,1) m. Where should an object of mass 40 kg be placed such that the centre of mass of this new system lies at (0,0,0)?
a) 3/2, 3/2, 3/2
b) -3/2, -3/2, -3/2
c) 3/4, 3/4, 3/4
d) -3/4, -3/4, -3/4
View Answer
Explanation: Sum of masses = 10 + 20 + 30 + 40 = 100
Since initial centre of mass is at (1,1,1), we can assume an object of 60 kg is at (1,1,1).
x-coordinate;
(60*1 + 40*x)/100 = 0
x = -3/2
y-coordinate;
(60*1 + 40*y)/100 = 0
y = -3/2
z-coordinate;
(60*1 + 40*z)/100 = 0
z = -3/2.
4. Masses 1 kg, 1.5 kg, 2 kg, and “M” kg are situated at (2,1,1), (1,2,1), (2,-2,1) and (-1,4,3). What is the value of “M” if their centre of mass is at (1,1,3/2)?
a) 1 kg
b) 1.5 kg
c) 2 kg
d) 2.5 kg
View Answer
Explanation: Sum of masses = 1 + 1.5 + 2 + M = 4.5 + M
x-coordinate;
(1*2 + 1.5*1 + 2*2 – M)/(4.5 + M) = 1
4.5 + M = 7.5 – M
2M = 3
M = 1.5 kg.
5.Particles of masses 1 kg and 3 kg are at (2i+5j+13k) m and (-6i+4j-2k) m. What is the position of their centre of mass?
a) 1/4 (-16i + 17j + 7k) m
b) 1/4 (-8i + 17j + 7k) m
c) 1/4 (-6i + 17j + 7k) m
d) 1/4 (-6i + 17j + 5k) m
View Answer
Explanation: Sum of masses = 1 + 3 = 4
x-coordinate;
(1*2-3*6)/4 = -16/4
y-coordinate;
(1*5 + 3*4)/4 = 17/4
z-coordinate;
(1*13-3*2)/4 = 7/4
Position of centre of mass = 1/4 (-6i + 17j + 5k) m.
6. Three objects of mass 1 kg each are placed at corners of a right-angled triangle AOB as shown in the figure. Consider ‘O’ as the origin and OA = OB = 1m. Determine the position of the centre of mass of this system.
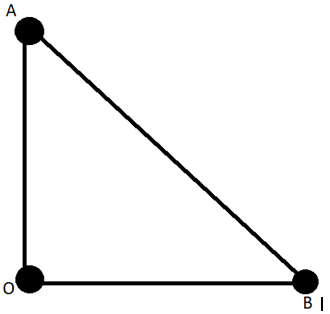
a) 1/3 (i- j) m
b) 2/3 (i + j) m
c) 1/3 (i+ j) m
d) (i- j) m
View Answer
Explanation: Sum of masses = 1 + 1 + 1 = 3
x-coordinate;
(1*0+1*0 + 1*1)/3 = 1/3
y-coordinate;
(1*1 + 1*0 + 1*0)/3 = 1/3
Position of centre of mass = 1/3 (i + j) m.
7.Four objects of mass 1 kg each are placed on 4 corners of a square of side 1 m as shown in the figure. Consider “O” to be the origin. What is the position of the centre of mass?
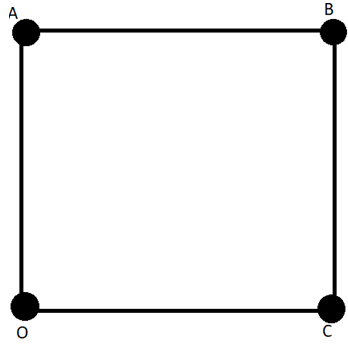
a) (i + j) m
b) 1/2 (i + j) m
c) (i– j) m
d) 1/2 (i – j) m
View Answer
Explanation: Sum of masses = 1 + 1 + 1 + 1 = 4
x-coordinate;
(1*0 + 1*1 + 1*1 + 1*0)/4 = 1/2
y-coordinate;
(1*1 + 1*1 + 1*0 + 1*0)/4 = 1/2
Position of centre of mass = 1/2 (i + j) m.
8. The distance between the centres of carbon and oxygen in the carbon monoxide molecules is 1.13 x 10-10 m. The distance of the centre of mass of the molecule relative to the oxygen atom is _____
a) 0.48 x 10-10 m
b) 0.64 x 10-10 m
c) 0.56 x 10-10 m
d) 0.36 x 10-10 m
View Answer
Explanation: The location of the centre of mass from an object in a two-object system is inversely proportional to the mass of the object.
The atomic mass of oxygen = 16
The atomic mass of carbon = 12
Total atomic mass = 16 + 12 = 28
The location of centre of mass relative to oxygen atom = (1.13 x 10-10) x 12 / 28
= 0.48 x 10-10 m.
9. Two particles of masses 2 kg and 3 kg are at rest and are separated by 10 m. If they move towards each other under the mutual force of attraction, they would meet at _____
a) 6 m from 4 kg body
b) 6 m from 6 kg body
c) 4 m from 4 kg body
d) 5 m from 6 kg body
View Answer
Explanation: The two bodies would meet at their centre of mass.
Sum of masses = 2 + 3 = 5 kg
Let us consider the 2 kg body as a reference;
The centre of mass from the 2 kg body =(3 x 10) / 5
= 6 m.
10. A ball of mass 3 kg and a ball of mass 2 kg roll towards each other on a flat surface. How far is the centre of mass from the 3 kg ball of the 2 balls are separated by 6 m?
a) 1.2 m
b) 2.4 m
c) 3.6 m
d) 4.8 m
View Answer
Explanation: Sum of masses = 3 + 2 = 5 kg
Centre of mass from 3 kg ball = (6 x 2) / 5
= 2.4 m.
11. A uniform disc of radius R is put over another uniform disc of radius 2R of same thickness and density. The edges of the two discs touch each other. What is the position of their centre of mass?
a) at 5R/3 from the centre of the larger disc
b) at 2R/3 from the centre of the larger disc
c) at 3R/5 from the centre of the larger disc
d) at 2R/5 from the centre of the larger disc
View Answer
Explanation:Since both discs have the same thickness and density;
M/(pi x R2 x t) = M’/((pi x 4 x R2 x t)
M = M’/4
M = Mass of a smaller disc
M’ = 4M = Mass of larger disc
Sum of masses = M + 4M = 5M
The distance of centres of discs = 3R
The distance of the centre of mass from larger disc = (3R x M)/5M
= 3R/5.
12. Three identical spheres each of radius R are placed such that their centres lie on a straight line. What is the location of their centre of mass from the centre of the first sphere?
a) R
b) 2R
c) 3R
d) 4R
View Answer
Explanation: Distance between first and last sphere = R + 2R + R = 4R
Since the spheres are identical and lie in a straight line, the centre of mass will lie exactly in the middle.
Hence the centre of mass lies at a distance of 2R from the centre of the first sphere.
13. The coordinates of the centre of mass of the system shown in the figures are _____
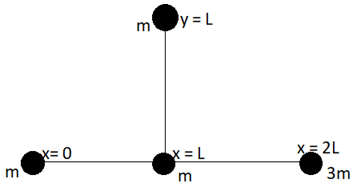
a) (0, 0)
b) (1.33L, 0.167L)
c) (L, L)
d) (0.33L, 1.67L)
View Answer
Explanation: Sum of masses = m + m + m + 3m = 6m
x-coordinate;
(m*0 + m*L + m*L + m*2L)/6m = 1.33L
y-coordinate;
(m*0 + m*L + m*0 + m*0)/6m = 0.167L.
14. From the figure, find out the perpendicular distance of the centre of mass of the system from side AB. ABCD is a square of side 2 m.
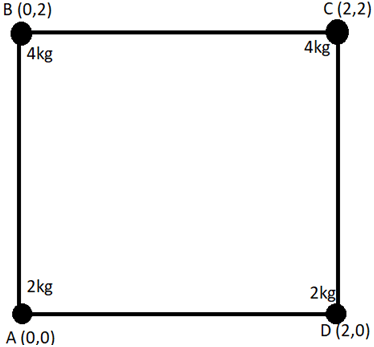
a) 1.33 m
b) 1 m
c) 1.5 m
d) 0.33 m
View Answer
Explanation:To find the perpendicular distance, we only need to find the y-coordinate.
Sum of masses = 4 + 4 + 2 + 2 = 12 kg
y-coordinate;
(2*0 + 4*2 + 4*2 + 2*0)/12 = 1.33 m.
15. Centre of mass can vary upon the application of internal force.
a) True
b) False
View Answer
Explanation: No, the centre of mass cannot vary upon the application of internal force. This is because internal force do not produce any net force. Hence the state of centre of mass in this scenario will remain unchanged.
More MCQs on Class 11 Physics Chapter 7:
- Chapter 7 – System of Particles and Rotational Motion MCQ (Set 2)
- Chapter 7 – System of Particles and Rotational Motion MCQ (Set 3)
- Chapter 7 – System of Particles and Rotational Motion MCQ (Set 4)
- Chapter 7 – System of Particles and Rotational Motion MCQ (Set 5)
- Chapter 7 – System of Particles and Rotational Motion MCQ (Set 6)
- Chapter 7 – System of Particles and Rotational Motion MCQ (Set 7)
- Chapter 7 – System of Particles and Rotational Motion MCQ (Set 8)
- Chapter 7 – System of Particles and Rotational Motion MCQ (Set 9)
- Chapter 7 – System of Particles and Rotational Motion MCQ (Set 10)
- Chapter 7 – System of Particles and Rotational Motion MCQ (Set 11)
To practice all chapters and topics of class 11 Physics, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
- Practice Class 11 - Biology MCQs
- Practice Class 12 - Physics MCQs
- Check Class 11 - Physics Books
- Practice Class 11 - Mathematics MCQs
- Practice Class 11 - Chemistry MCQs
