This set of Casting, Forming and Welding Multiple Choice Questions & Answers (MCQs) focuses on “Functions of a Pattern”.
1. Which of the following is not a part of the pattern at most times?
a) Mould cavity
b) Cope
c) Molten metal
d) Core
View Answer
Explanation: Molten material is poured into the mould cavity to make a casting, after solidification and hence, it does not constitute the pattern.
2. Which of the following does not serve the purpose of using patterns in sand casting?
a) Contain core prints if the casting requires a core and need to be made hollow
b) To give the exact shape and size (in addition to the allowances) to the casting as that of the final object
c) Reduces the cost of production while used in mass production
d) Sometimes used to carry the mechanism to melt the metal/material which is to be poured into the cavity
View Answer
Explanation: The pattern never carries or includes the mechanism to melt the metal, which needs to be poured into the cavity. This job needs to be done externally.
3. Name the missing part of the pattern in the diagram labelled as (?)?
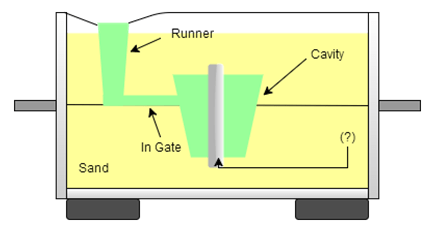
a) Core
b) Riser
c) Sprue
d) Mould cavity
View Answer
Explanation: The illustrated part in the diagram is core. The core in a pattern is used to create holes or hollow cavities.
4. The function of a gated pattern is ___________
a) To produce small castings in mass production
b) To create castings of a very heavy mass
c) To create castings containing complex design
d) To create symmetrical castings
View Answer
Explanation: Gated pattern manufactures huge no. of products using single time casting using a common gating inlet system. Hence, the casting needs to be small and simple and is only justified for mass production, as the pattern is used for 1-2 times only.
5. Which of the following factors affect the choice of a pattern at most times?
a) Size and complexity of the casting
b) Characteristics of castings
c) Type of molding and castings method to be used
d) Type of cooling rates to be provided
View Answer
Explanation: The type of cooling rates depends upon the required strength in the casting, which cannot be controlled by the type of any pattern. Proper chills are to be used for that purpose.
6. Which of the following sequence is in the correct order to prepare a cast using the sand casting method?
[1] Mould making [2] Clamping [3] Pouring [4] Cooling [5] Trimming [6] Removal
a) 1,3,2,4,6,5
b) 2,1,3,4,5,6
c) 1,2,3,4,5,6
d) 1,2,3,4,6,5
View Answer
Explanation: For a proper casting to be carried out, the correct order in which processes are to be executed out starts with mould making then clamping it then pouring the metal then cooling then removing it and at last trimming it or providing machining.
7. What is a function of a riser in a sand casting?
a) Provide good mobility to the molten metal
b) Prevent cavities due to shrinkage
c) To develop holes or hollow cavities in the casting
d) To provide differential cooling rates in specific areas of the casting
View Answer
Explanation: The risers also known as feeders are used to decrease the phenomena of shrinkage during solidification of the molten metal.
8. Runners, gates and risers are attached to the pattern to __________
a) Provide ease of cooling
b) Provide feed to the molten material
c) Provide design to the casting
d) Enhance the finishing of the casting
View Answer
Explanation: These external elements are added to the pattern or mould cavity to enhance the flow of molten metal, hence, to enhance the casting process.
Sanfoundry Global Education & Learning Series – Casting, Forming and Welding.
To practice all areas of Casting, Forming and Welding, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
- Apply for Metallurgical Engineering Internship
- Apply for Mechanical Engineering Internship
- Practice Metallurgical Engineering MCQs
- Check Casting, Forming and Welding I Books
- Practice Casting, Forming and Welding II MCQ
