This set of Casting, Forming and Welding Multiple Choice Questions & Answers (MCQs) focuses on “Hand Molding Equipment”.
1. Which of the following is not a hand molding process?
a) Air cooling
b) Ramming
c) Placing
d) Turning over
View Answer
Explanation: Among the following processes, air cooling is not a type of hand molding process, while the remaining other processes are hand molding processes.
2. How apart should gaggers be located?
a) 65mm
b) 70mm
c) 75mm
d) 80mm
View Answer
Explanation: A gagger is made up of steel reinforced bar. These gaggers should be located at a distance of 75mm from each other.
3. At what distance should the gagger be kept from the pattern?
a) 3mm
b) 6mm
c) 9mm
d) 12mm
View Answer
Explanation: The distance between a gagger and a pattern should be about 6mm so that it is within the reach of the pattern.
4. The following figure represents which hand molding equipment?
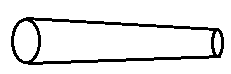
a) Bellow
b) Sprue pin
c) Spirit level
d) Swab
View Answer
Explanation: The hand molding equipment here is a sprue pin. A tapering is provided to the pin, that is, the diameter of the pin keeps increasing from one end to another.
5. The following figure represents which hand molding equipment?

a) Pipe smoother
b) Button smoother
c) Spirit level
d) Swab
View Answer
Explanation: The hand molding equipment which is shown in the figure is a button smoother. They ensure the repairing work of the casts. Not just that, they also help in the finishing work.
6. The following figure represents which hand molding equipment?
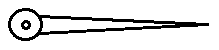
a) Gagger
b) Draw spike
c) Peen rammer
d) Swab
View Answer
Explanation: The hand molding equipment which is shown in the figure is a draw spike. It is a sharp tapered rod, that is, the diameter of the rod goes on increasing from the tip till the end.
7. The following figure represents which hand molding equipment?
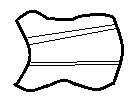
a) Gate cutter
b) Draw spike
c) Swab
d) Hand riddle
View Answer
Explanation: In the given figure of the hand molding equipment which is shown is a gate cutter. A gate cutter is basically a sheet metal which is given a definite shape, so as to be able to perform proper cutting operations.
8. The following figure represents which hand molding equipment?
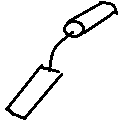
a) Trowel
b) Vent wire
c) Spirit level
d) Swab
View Answer
Explanation: The hand molding equipment which is shown in the figure is a trowel. It is used for flat finish of the mold surface. These are basically used for cutting ingates.
9. The following figure represents which hand molding equipment?
![]()
a) Trowel
b) Vent wire
c) Spirit level
d) Swab
View Answer
Explanation: The hand molding equipment here is a vent wire. It has a spiked tool and a handle at the back. It is mainly used for making holes in sand.
10. Hand rammer is made up of metal.
a) True
b) False
View Answer
Explanation: Hand rammers are used for ramming sand in bench mold. It can be made up of either metal or it could be of wood too. The material depends on the type of operation.
Sanfoundry Global Education & Learning Series – Casting, Forming and Welding.
To practice all areas of Casting, Forming and Welding, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
- Apply for Metallurgical Engineering Internship
- Check Casting, Forming and Welding I Books
- Check Mechanical Engineering Books
- Practice Casting, Forming and Welding II MCQ
- Practice Metallurgical Engineering MCQs
