This set of Soil Mechanics Multiple Choice Questions & Answers (MCQs) focuses on “Stress Distribution – Triangular Loadings”.
1. The uniformly varying load is __________ in a beam.
a) rate of loading increases linearly from zero
b) rate of loading increases non-linearly from zero
c) equal load at every point
d) equal load only at supports
View Answer
Explanation: The uniformly varying load is the rate of loading which increases linearly from zero at one end of the support.
2. The triangular load is also known as ___________
a) uniformly distributed load
b) uniformly varying load
c) point load
d) equivalent uniformly distributed load
View Answer
Explanation: The triangular load is also known as uniformly varying load. The uniformly varying load is the rate of loading which increases linearly from zero at one end of the support.

3. For any position of point P subtending angle α with AB, the vertical stress is given by___________
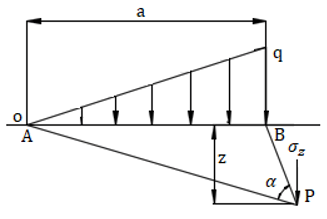
a) \(σ_z=\frac{q}{aπ} [xα(x-α)] \)
b) \(σ_z=\frac{q}{aπ} \)
c) \(σ_z=\frac{q}{aπ}\left[xα-\frac{az}{(x-α)^2+z^2}(x-α)\right] \)
d) \(σ_z= \left[xα-\frac{az}{(x-α)^2+z^2}(x-α)\right] \)
View Answer
Explanation: For any position of point P subtending angle α with AB, the vertical stress is given by,
\(σ_z=\frac{q}{aπ}\left[xα-\frac{az}{(x-α)^2+z^2}(x-α)\right] \)
Where, σz= vertical stress
x=distance from the support A
z=depth from the ground surface
q=load applied.
4. For point P under the support A, the vertical stress is given by __________

a) \(σ_z=\frac{q}{aπ} [xα(x-α)] \)
b) \(σ_z=\frac{q}{aπ} \)
c) \(σ_z=\frac{q}{π} \left[\frac{az}{a^2+z^2}\right] \)
d) \(σ_z=\left[xα-\frac{az}{(x-α)^2+z^2}(x-α)\right] \)
View Answer
Explanation: For point P under the support A, the vertical stress is given by,
\(σ_z=\frac{q}{π} \frac{sin2α_A}{2} \)
∴ \(σ_z=\frac{q}{π} \left[\frac{az}{a^2+z^2}\right]. \)
5. For point P under the support B, the vertical stress is given by __________

a) \(σ_z=\frac{q}{aπ} [xα(x-α)] \)
b) \(σ_z=\frac{q}{π}α_B \)
c) \(σ_z=\frac{q}{π} \left[\frac{az}{a^2+z^2}\right] \)
d) \(σ_z=\left[xα_B-\frac{az}{(x-α_B )^2+z^2}(x-α_B)\right] \)
View Answer
Explanation: For point P under the support B, the vertical stress is given by,
\(σ_z=\frac{q}{π}α_B \)
Where α_B=angle subtended from point P below the support B to the line AB
q=load applied.
6. For a linearly variable infinite load, for a point P, the vertical stress σz is _________
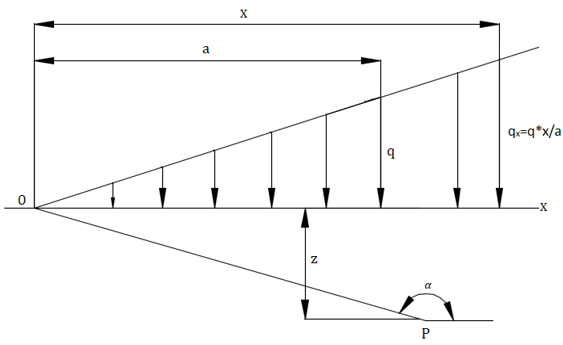
a) \(σ_z=\frac{q}{aπ} \left[xα+z\right] \)
b) \(σ_z=\frac{q}{aπ} \)
c) \(σ_z=\frac{q}{π}\left[\frac{az}{a^2+z^2}\right] \)
d) \(σ_z=\left[xα-\frac{az}{(x-α)^2+z^2}(x-α)\right] \)
View Answer
Explanation: let the load intensity be q at a horizontal distance a and the load intensity at distance x is qx=q*x/a.
∴ for any point P the load is given by, \(σ_z=\frac{q}{aπ} \left[xα+z\right]. \)
7. For a symmetrically distributed triangular load, under the centre of the triangular load, the vertical stress at any point at a depth z is given by ___________
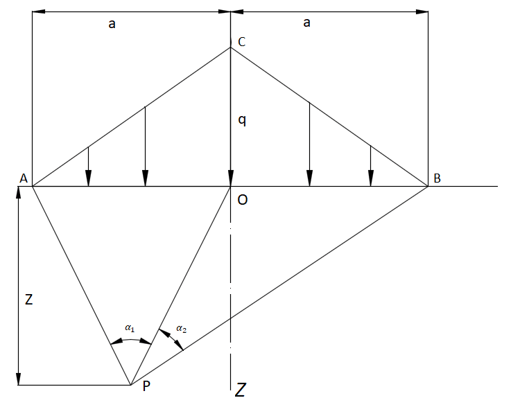
a) \(σ_z=\frac{q}{aπ} \left[α_1+α_2 \right] \)
b) \(σ_z=\frac{q}{π} \left[α_1+α_2 \right]\)
c) \(σ_z=\frac{q}{π} \left[\frac{az}{a^2+z^2}\right]\)
d) \(σ_z=\frac{q}{π} \left[α_1-α_2 \right]\)
View Answer
Explanation: Considering two triangular loads of AOC and OCB separately and adding them we get,
\(σ_{z1}=\frac{q}{π} α_1\) for triangular load of AOC
\(σ_{z2}=\frac{q}{π} α_2\) for triangular load of OCB
∴ \(σ_z=σ_{z1}+σ_{z2}\)
∴ \(σ_z=\frac{q}{π} \left[α_1+α_2\right].\)
8. For a symmetrically distributed triangular load, the shear stress τxz at any point at a depth z is given by ___________

a) \(τ_{xz}=-\frac{qz}{aπ} \left[α_1-α_2 \right] \)
b) \(τ_{xz}=-\frac{q}{π} \left[α_1+α_2 \right]\)
c) \(τ_{xz}=-\frac{q}{π} \left[\frac{az}{a^2+z^2}\right]\)
d) \(τ_{xz}=-\frac{q}{π} \left[α_1-α_2 \right] \)
View Answer
Explanation: For a symmetrically distributed triangular load, the shear stress τxz at any point at a depth z is given by,
\(τ_{xz}=-\frac{qz}{aπ} \left[α_1-α_2 \right] \)where α1 and α2 are angles subtended by the point P at AO and BO respectively
z=depth.
9. For a triangular and uniformly distributed semi-infinite loads, the shear stress τxz in the plane xz is ___________
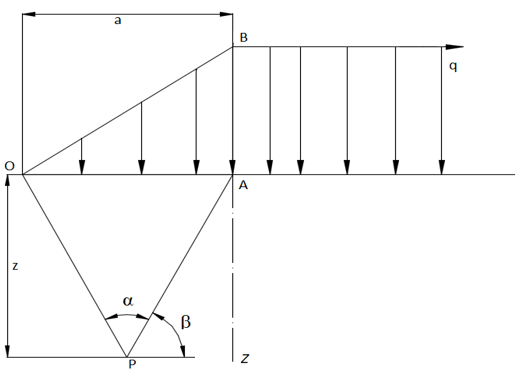
a) \(τ_{xz}=-\frac{qz}{aπ} α \)
b) \(τ_{xz}=-\frac{q}{π} α\)
c) \(τ_{xz}=-\frac{q}{π} \left[\frac{az}{a^2+z^2}\right]\)
d) \(τ_{xz}=-\frac{q}{π} z\)
View Answer
Explanation: For a triangular and uniformly distributed semi-infinite loads, the shear stress τxz in the plane xz is given by,
\(τ_{xz}=-\frac{qz}{aπ}\) α where α is the angle subtended by point P on OA,
z=depth
q=load intensity.
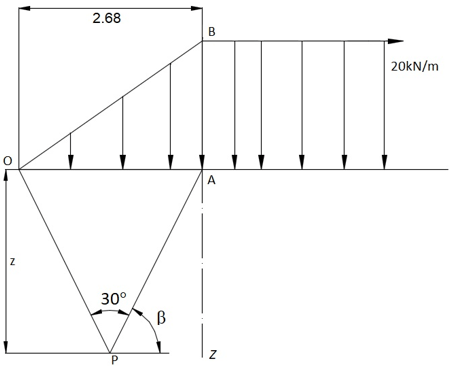
10. For a load intensity of q=20kN/m, find the shear stress τxz at a depth 5m from the given diagram.
a) -5.2 kN/m2
b) -6.2 kN/m2
c) -7.2 kN/m2
d) -8.2 kN/m2
View Answer
Explanation: Given,
Load q=20kN/m
α=30°=0.523rad
a=2.68m
z=5m
∴ \(τ_{xz} =-\frac{qz}{aπ} α\)
\(τ_{xz}=-\frac{20*5}{2.68*π}0.523\)
τxz=-6.2 kN/m2.
11. For a triangular and uniformly distributed semi-infinite loads, the vertical stress σz is given by ___________

a) \(σ_z=\frac{q}{aπ}[xα+z] \)
b) \(σ_z=\frac{q}{aπ}(aβ+xα) \)
c) \(σ_z=\frac{q}{π} \left[\frac{az}{a^2+z^2}\right]\)
d) \(σ_z=[xα-\frac{az}{(x-α)^2+z^2}(x-α)]\)
View Answer
Explanation: For a triangular and uniformly distributed semi-infinite loads, the vertical stress σz is given by,
\(σ_z=\frac{q}{aπ}(aβ+xα) \) where α is the angle subtended by point P on OA,
β= angle at point P between horizontal line and PA
q=load intensity.
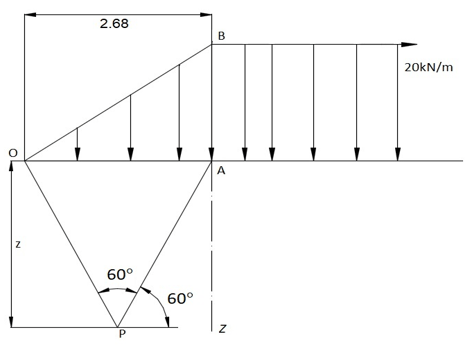
12. For a load intensity of q=20kN/m, find the vertical stress σz from the given diagram.
a) 5.62 kN/m2
b) 6.23 kN/m2
c) 13.33 kN/m2
d) 8.32 kN/m2
View Answer
Explanation: Given,
Load q=20kN/m
α=60°=1.047rad
β=60°=1.047rad
a=2.68m
the vertical stress σz is,
\(σ_z=\frac{q}{aπ}(aβ+xα) \)
\(σ_z=\frac{20}{2.68*π}(2.68*1.047+2.68*1.047)\)
∴ σz=13.33 kN/m2.
13. Trapezoidal load is encountered in earth fills.
a) True
b) False
View Answer
Explanation: Trapezoidal loadings are quite commonly encountered in earth fills, embankments, highways, rail road, earth dams, etc. The trapezoidal loadings can be split into a triangular loading minus another triangular loading of smaller magnitude.
14. The maximum shear stress is the difference between major and minor principal stresses.
a) True
b) False
View Answer
Explanation: The maximum shear stress is half the difference between major and minor principal stresses.
\(τ_{max}=\frac{1}{2}(σ_1-σ_2).\)
15. The greatest value of maximum shear stress τmax occurs when angle θ is _________
a) π
b) π/2
c) π/3
d) π/4
View Answer
Explanation: The maximum shear stress is given by,
\(τ_{max}=\frac{1}{2} (σ_1-σ_2 )=\frac{q}{π} sinθ\)
Sinθ is maximum when θ= π/2
∴ Sin π/2=1
∴ \(τ_{max}=\frac{q}{π}.\)
Sanfoundry Global Education & Learning Series – Soil Mechanics.
To practice all areas of Soil Mechanics, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
- Apply for Civil Engineering Internship
- Practice Civil Engineering MCQs
- Practice Geotechnical Engineering II MCQs
- Check Geotechnical Engineering I Books
- Check Civil Engineering Books
