This set of Soil Mechanics Multiple Choice Questions & Answers (MCQs) focuses on “Stress Distribution – Vertical and Horizontal Pressure”.
1. In simple radial distribution, the three stress components σr, σθ and τrθ are given by ___________
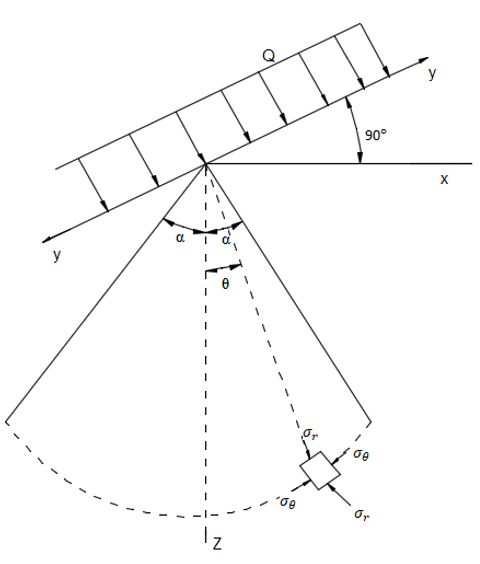
a) \(σ_r=K \frac{Q cosθ}{r}, σ_θ=0 \,and\, τ_{rθ}=0 \)
b) σr=KQ, σθ=0 and τrθ=0
c) \(σ_r=\frac{Q cosθ}{r}, σ_θ=0 \,and\, τ_{rθ}=0\)
d) σr=0, σθ=0 and τrθ= 0
View Answer
Explanation: At any radial distance r and polar angle θ, Mitchell found that the three stress components σr, σθ and τrθ are given by,
\(σ_r=K \frac{Q cosθ}{r}, σ_θ=0 \,and\, τ_{rθ}=0. \)
Where K is a constant to be found by boundary conditions. The above solution is valid only if it satisfies the equilibrium equations and the compatibility equation.
2. The equilibrium equation in polar coordinates is given by _____________
a) \(\frac{1}{r} \frac{∂τ_{rθ}}{∂θ}+\frac{σ_r-σ_θ}{r}=0\)
b) \(\frac{∂σ_r}{∂r}+\frac{∂τ_{rθ}}{∂θ}+\frac{σ_r-σ_θ}{r}=0\)
c) \(\frac{∂σ_r}{∂r}+\frac{1}{r} \frac{∂τ_{rθ}}{∂θ}+\frac{σ_r-σ_θ}{r}=0\)
d) \(\frac{∂σ_r}{∂r}+\frac{1}{r} \frac{∂τ_{rθ}}{∂θ}=0\)
View Answer
Explanation: The equilibrium equations in polar coordinates are given by,
1. \(\frac{∂σ_r}{∂r}+\frac{1}{r} \frac{∂τ_{rθ}}{∂θ}+\frac{σ_r-σ_θ}{r}=0 \)
2. \(\frac{1}{r}\frac{∂σ_θ}{∂θ}+\frac{∂τ_{rθ}}{∂r}+\frac{2τ_{rθ}}{r}=0.\)
3. The equilibrium equation in polar coordinates is given by _____________
a) \(\frac{1}{r} \frac{∂τ_{rθ}}{∂θ}+\frac{σ_r-σ_θ}{r}=0\)
b) \(\frac{∂σ_r}{∂r}+\frac{∂τ_{rθ}}{∂θ}+\frac{σ_r-σ_θ}{r}=0\)
c) \(\frac{∂σ_r}{∂r}+\frac{1}{r} \frac{∂τ_{rθ}}{∂θ}+\frac{σ_r-σ_θ}{r}=0\)
d) \(\frac{∂σ_r}{∂r}+\frac{1}{r} \frac{∂τ_{rθ}}{∂θ}=0\)
View Answer
Explanation: The equilibrium equations in polar coordinates are given by,
1. \(\frac{∂σ_r}{∂r}+\frac{1}{r} \frac{∂τ_{rθ}}{∂θ}+\frac{σ_r-σ_θ}{r}=0 \)
2. \(\frac{1}{r}\frac{∂σ_θ}{∂θ}+\frac{∂τ_{rθ}}{∂r}+\frac{2τ_{rθ}}{r}=0.\)
4. The compatibility equation in terms of stress components in polar coordinates are given by ____________
a) \((\frac{∂^2}{∂r^2} +\frac{1}{r} \frac{∂}{∂r}+\frac{1}{r^2} \frac{∂^2}{∂θ^2} )(σ_r+σ_θ )=0\)
b) \((\frac{∂^2}{∂r^2} +\frac{1}{r} \frac{∂}{∂r}+\frac{1}{r^2} \frac{∂^2}{∂θ^2} )(σ_θ )=0\)
c) \((\frac{∂^2}{∂r^2} +\frac{1}{r} \frac{∂}{∂r}+\frac{1}{r^2} \frac{∂^2}{∂θ^2} )(σ_r )=0\)
d) \((\frac{∂^2}{∂r^2} +\frac{1}{r} \frac{∂}{∂r}+\frac{1}{r^2} \frac{∂^2}{∂θ^2} )(σ_r+σ_θ )=1\)
View Answer
Explanation: The compatibility equation is the additional equation to solve the stress problem. The compatibility equation in terms of stress components in polar coordinates are given by,
\((\frac{∂^2}{∂r^2} +\frac{1}{r} \frac{∂}{∂r}+\frac{1}{r^2} \frac{∂^2}{∂θ^2} )(σ_r+σ_θ )=0.\)
5. In simple radial distribution, if \(σ_r=K \frac{Q cosθ}{r},\) then the value of K is ________

a) K=\(\frac{2}{2α+sin2α}\)
b) K=2α+sinα
c) K=2α-sinα
d) K=sinα
View Answer
Explanation: Considering the equilibrium of the wedge aob,
We have \(KQ(α+\frac{1}{2} sin2α)=Q\)
∴ K=\(\frac{2}{2α+sin2α}.\)
6. When the ground is horizontal, \(α=\frac{π}{2}\) in constant K. What will be the radial stress σr due to vertical line load?

a) \(σ_r=\frac{Q cosθ}{r}\)
b) \(σ_r=\frac{2Q cosθ}{πr}\)
c) \(σ_r=\frac{Q sinθ}{r}\)
d) \(σ_r=\frac{2Q sinθ}{r}\)
View Answer
Explanation: At any radial distance r and polar angle θ, Mitchell found that the radial stress component σr is given by,
\(σ_r=K\frac{Q cosθ}{r} \,where\, K=\frac{2}{2α+sin2α}\)
When the ground is horizontal =\(\frac{π}{2},\)
∴ \(σ_r=\frac{2Q cosθ}{πr}.\)
7. The relation between the stress component in x-direction on a horizontal plane in Cartesian coordinates and polar coordinates for vertical line load is ___________
a) σx=σr tan2θ
b) σx=σr cosec2θ
c) σx=σr cosθ
d) σx=σr sin2θ
View Answer
Explanation: From the figure,

On a horizontal plane, the relation between the stress component in x-direction in Cartesian coordinates and polar coordinates is,
σx=σr sin2θ.
8. The relation between the stress component in z-direction on a horizontal plane in Cartesian coordinates and polar coordinates for vertical line load is ___________
a) σz=σr cos2θ
b) σz=σr cosec2θ
c) σz=σr cosθ
d) σz=σr sin2θ
View Answer
Explanation: From the figure,

On a horizontal plane, the relation between the stress component in z-direction in Cartesian coordinates and polar coordinates is,
σz=σr cos2θ.
9. The relation between the shear stress component in xz-plane in Cartesian coordinates and polar coordinates for vertical line load is ___________
a) τxz=σr tan2θ
b) τxz=σr cosec2θ
c) τxz=σr sinθcosθ
d) τxz=σr sin2θ
View Answer
Explanation: From the figure,

On xz-plane , the relation between the shear stress component in Cartesian coordinates and polar coordinates is,
τxz=σr sinθcosθ.
10. The stress component in x-direction on a horizontal plane in Cartesian coordinates for horizontal line load is ___________
a) \(σ_x=\frac{2Q}{xzsinθcosθ} \)
b) \(σ_x=\frac{2Qxz^2}{π(x^2+z^2)^2} \)
c) \(σ_x=\frac{2Qx^3}{π(x^2+z^2)^2} \)
d) \(σ_x=\frac{2Qx^2 z}{π(x^2+z^2)^2} \)
View Answer
Explanation: On a horizontal plane, the relation between the stress component in x-direction in Cartesian coordinates and polar coordinates is,
\(σ_x=σ_r sin^2θ \,where\, σ_r=K \frac{Q cosθ}{r}\)
And \(K=\frac{2}{2α+sin2α}\)
∴ \(σ_x=\frac{2Qx^3}{π(x^2+z^2)^2}. \)
11. The stress component in x-direction on a horizontal plane in Cartesian coordinates for horizontal line load is ___________
a) \(σ_x=\frac{2Q}{xzsinθcosθ} \)
b) \(σ_x=\frac{2Qxz^2}{π(x^2+z^2)^2} \)
c) \(σ_x=\frac{2Qx^3}{π(x^2+z^2)^2} \)
d) \(σ_x=\frac{2Qx^2 z}{π(x^2+z^2)^2} \)
View Answer
Explanation: On a horizontal plane, the relation between the stress component in z-direction in Cartesian coordinates and polar coordinates is,
\(σ_z=σ_r cos^2θ \,where\, σ_r=K \frac{Q cosθ}{r} \)
And \(K=\frac{2}{2α+sin2α}\)
∴ \(σ_x=\frac{2Qx^3}{π(x^2+z^2 )^2}.\)
12. The shear stress component in xz-plane in Cartesian coordinates for horizontal line load is ___________
a) \(τ_{xz}=\frac{2Q}{xzsinθcosθ} \)
b) \(τ_{xz}=\frac{2Qxz^2}{π(x^2+z^2)^2} \)
c) \(τ_{xz}=\frac{2Qx^3}{π(x^2+z^2)^2} \)
d) \(τ_{xz}=\frac{2Qx^2 z}{π(x^2+z^2)^2} \)
View Answer
Explanation: On a xz-plane, the relation between the shear stress component in Cartesian coordinates and polar coordinates is,
\(τ_{xz}=σ_r sinθcosθ \,where\, σ_r=K \frac{Q cosθ}{r}\)
And \(K=\frac{2}{2α+sin2α}\)
∴\(τ_{xz}=\frac{2Qx^2 z}{π(x^2+z^2)^2}. \)
13. The radial stress component σr due to inclined line load of intensity Q per unit length is given by ___________

a) \(σ_r=\frac{2Q}{r}(\frac{cosβcosθ}{2α+sin2α})\)
b) \(σ_r=\frac{2Q}{r} (\frac{cosβcosθ}{2α+sin2α}+\frac{sinβsinθ}{2α-sin2α})\)
c) \(σ_r=\frac{Q}{r} (\frac{cosβcosθ}{2α+sin2α}+\frac{sinβsinθ}{2α-sin2α})\)
d) \(σ_r=\frac{2Q}{r}(\frac{sinβsinθ}{2α-sin2α})\)
View Answer
Explanation: The stresses due to inclined load of intensity Q per unit length can be found by resolving the inclined load into horizontal and vertical components, we get,
\(σ_r=\frac{2Q}{r} (\frac{cosβcosθ}{2α+sin2α}+\frac{sinβsinθ}{2α-sin2α}).\)
14. When the ground is horizontal, \(α=\frac{π}{2}\) in constant K. What will be the radial stress σr due to inclined line load at the horizontal ground surface?

a) \(σ_r=\frac{Q cosθ}{r}\)
b) \(σ_r=\frac{2Q cos(θ-β)}{πr}\)
c) \(σ_r=\frac{Q sinθ}{r}\)
d) \(σ_r=\frac{2Q sinθ}{r}\)
View Answer
Explanation: At any radial distance r and polar angle θ, the radial stress component σr due to inclined line load is given by,
\(σ_r=\frac{2Q}{r} (\frac{cosβcosθ}{2α+sin2α}+\frac{sinβsinθ}{2α-sin2α}).\)
When the ground is horizontal =\(\frac{π}{2}\),
∴ \(σ_r=\frac{2Q cos(θ-β)}{πr}.\)
Sanfoundry Global Education & Learning Series – Soil Mechanics.
To practice all areas of Soil Mechanics, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
- Practice Geotechnical Engineering II MCQs
- Practice Civil Engineering MCQs
- Check Geotechnical Engineering I Books
- Apply for Civil Engineering Internship
- Check Civil Engineering Books
