This set of Soil Mechanics Multiple Choice Questions & Answers (MCQs) focuses on “Elasticity – Equilibrium Equations”.
1. The normal stress component acting at the centre, in the given diagram, will be _________ to the face (B D D1 B1).
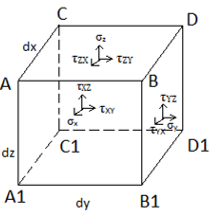
a) increased to \((σ_y+\frac{∂σ_y}{∂y}\frac{dy}{2}) \)
b) decreased to \((σ_y-\frac{∂σ_y}{∂y}\frac{dy}{2}) \)
c) equal to σY
d) equal to σz
View Answer
Explanation: The stress on each face will be equal to the stress at the centre, increased, if the face is along the direction of stress, by the distance to the centre to the face times the spatial derivative of the stress. Therefore on face (B D D1 B1), the stresses is \((σ_y+\frac{∂σ_y}{∂y}\frac{dy}{2}) \) .
2. The normal stress component acting at the centre, in the given diagram, will be _________ to the face (A C C1 A1).

a) increased to \((σ_y+\frac{∂σ_y}{∂y}\frac{dy}{2}) \)
b) decreased to \((σ_y-\frac{∂σ_y}{∂y}\frac{dy}{2}) \)
c) equal to σY
d) equal to σz
View Answer
Explanation: The stress on each face will be equal to the stress at the centre, decreased, if the face is opposite to the direction of stress, by the distance to the centre to the face times the spatial derivative of the stress. Therefore on face (A C C1 A1), the stresses is \((σ_y-\frac{∂σ_y}{∂y}\frac{dy}{2}). \)
3. The equilibrium equation obtained by summing all forces on x-direction is ________
a) \(\frac{∂σ_x}{∂x} + \frac{∂τ_{yx}}{∂y} + \frac{∂τ_{zx}}{∂z} +X=0\)
b) \(\frac{∂τ_{xy}}{∂x} + \frac{∂σ_y}{∂y} +\frac{∂τ_{zy}}{∂z}+Y=0\)
c) \(\frac{∂τ_{xz}}{∂x} +\frac{∂τ_{yz}}{∂y} +\frac{∂σ_z}{∂z} +Z=0\)
d) \(\frac{∂σ_x}{∂x}+\frac{∂τ_{yx}}{∂y} +\frac{∂τ_{zx}}{∂z} = 0\)
View Answer
Explanation: The sum of forces acting on the element in the x-direction is given by,
\(\{(σ_x+\frac{∂σ_x}{∂x} \frac{dx}{2})dy.dz-(σ_x-\frac{∂σ_x}{∂x}\frac{dx}{2})dy.dz\} +
\{(τ_{yx}+\frac{∂τ_{yx}}{∂y} \frac{dy}{2})dx.dz-(τ_{yx}-\frac{∂τ_{yx}}{∂y}\frac{dy}{2})dx.dz\} + \)
\(\{(τ_{zx}+\frac{∂τ_{zx}}{∂z}\frac{dz}{2})dx.dy-(τ_{zx}-\frac{∂τ_{zx}}{∂z}\frac{dz}{2})dx.dy\} + Xdx.dy.dz = 0\)
Now dividing all the terms by dx.dy.dz we get,
\(\frac{∂σ_x}{∂x} + \frac{∂τ_{yx}}{∂y} + \frac{∂τ_{zx}}{∂z} +X=0.\)
4. The equilibrium equation obtained by summing all forces on y-direction is ________
a) \(\frac{∂σ_x}{∂x} + \frac{∂τ_{yx}}{∂y} + \frac{∂τ_{zx}}{∂z} +X=0\)
b) \(\frac{∂τ_{xy}}{∂x} + \frac{∂σ_y}{∂y} +\frac{∂τ_{zy}}{∂z}+Y=0\)
c) \(\frac{∂τ_{xz}}{∂x} +\frac{∂τ_{yz}}{∂y} +\frac{∂σ_z}{∂z} +Z=0\)
d) \(\frac{∂σ_x}{∂x}+\frac{∂τ_{yx}}{∂y} +\frac{∂τ_{zx}}{∂z} = 0\)
View Answer
Explanation: The sum of forces acting on the element in the y-direction is given by,
\(\{(σ_y+\frac{∂σ_y}{∂y} \frac{dy}{2})dx.dz-(σ_y-\frac{∂σ_y}{∂y}\frac{dy}{2})dx.dz\} +
\{(τ_{zy}+\frac{∂τ_{zy}}{∂z} \frac{dz}{2})dy.dx-(τ_{zy}-\frac{∂τ_{zy}}{∂z}\frac{dz}{2})dy.dx\} + \)
\(\{(τ_{xy}+\frac{∂τ_{xy}}{∂x}\frac{dx}{2})dy.dz-(τ_{xy}-\frac{∂τ_{xy}}{∂x}\frac{dx}{2})dy.dz\} + Ydx.dy.dz = 0\)
Now dividing all the terms by dx.dy.dz we get,
\(\frac{∂τ_{xy}}{∂x} + \frac{∂σ_y}{∂y} +\frac{∂τ_{zy}}{∂z}+Y=0.\)
5. The equilibrium equation obtained by summing all forces on z-direction is ________
a) \(\frac{∂σ_x}{∂x} + \frac{∂τ_{yx}}{∂y} + \frac{∂τ_{zx}}{∂z} +X=0\)
b) \(\frac{∂τ_{xy}}{∂x} + \frac{∂σ_y}{∂y} +\frac{∂τ_{zy}}{∂z}+Y=0\)
c) \(\frac{∂τ_{xz}}{∂x} +\frac{∂τ_{yz}}{∂y} +\frac{∂σ_z}{∂z} +Z=0\)
d) \(\frac{∂σ_x}{∂x}+\frac{∂τ_{yx}}{∂y} +\frac{∂τ_{zx}}{∂z} = 0\)
View Answer
Explanation: The sum of forces acting on the element in the z-direction is given by,
\(\{(σ_z+\frac{∂σ_z}{∂z}\frac{dz}{2})dx.dy-(σ_z-\frac{∂σ_z}{∂z} \frac{dz}{2})dx.dy\} +
\{(τ_{zx}+\frac{∂τ_{zx}}{∂x} \frac{dx}{2})dz.dy-(τ_{zx}-\frac{∂τ_{zx}}{∂x}\frac{dx}{2})dz.dy\} +\)
\( \{(τ_{yz}+\frac{∂τ_{yz}}{∂y} \frac{dy}{2})dz.dx-(τ_{yz}-\frac{∂τ_{yz}}{∂y}\frac{dy}{2})dz.dx\} + Zdx.dy.dz = 0\)
Now dividing all the terms by dx.dy.dz we get,
\(\frac{∂τ_{xz}}{∂x} +\frac{∂τ_{yz}}{∂y} +\frac{∂σ_z}{∂z} +Z=0.\)
6. The problem of elasticity is _________
a) strictly determinate
b) strictly indeterminate
c) in some cases indeterminate
d) cannot be classified as determinate or indeterminate
View Answer
Explanation: There are six independent stresses components acting at a point and the complete solution of the problem requires the determination of these six unknown stress components. Since there are only three equilibrium equations available, the problem of elasticity is strictly of indeterminate nature.
7. The three equations of static equilibrium of the problem of elasticity are not sufficient to solve the six unknown stress components.
a) True
b) False
View Answer
Explanation: The problem of elasticity is strictly of indeterminate nature. To solve for unknowns, it should be supplemented with equations of compatibility of deformations.
8. The equilibrium equations in terms of total stresses formed by summing all forces on x-direction is ________
a) \(\frac{∂σ_x}{∂x} + \frac{∂τ_{yx}}{∂y} + \frac{∂τ_{zx}}{∂z} +X=0\)
b) \(\frac{∂τ_{xy}}{∂x} + \frac{∂σ_y}{∂y} +\frac{∂τ_{zy}}{∂z}+Y=0\)
c) \(\frac{∂τ_{xz}}{∂x} +\frac{∂τ_{yz}}{∂y} +\frac{∂σ_z}{∂z} +Z=0\)
d) \(\frac{∂σ_x}{∂x}+\frac{∂τ_{yx}}{∂y} +\frac{∂τ_{zx}}{∂z} = 0\)
View Answer
Explanation: The equilibrium equations in terms of total stresses formed by summing all forces on x-direction will include seepage force; the body forces will be equal to those due to gravity in respective directions.
∴X=0,
The equilibrium equation obtained by summing all forces on x-direction is,
\(\frac{∂σ_x}{∂x} + \frac{∂τ_{yx}}{∂y} + \frac{∂τ_{zx}}{∂z} +X=0\)
Therefore, the equilibrium equations in terms of total stresses formed by summing all forces on x-direction is,
\(\frac{∂σ_x}{∂x}+\frac{∂τ_{yx}}{∂y} +\frac{∂τ_{zx}}{∂z} = 0.\)
9. The equilibrium equations in terms of total stresses formed by summing all forces on y-direction is ________
a) \(\frac{∂σ_x}{∂x} + \frac{∂τ_{yx}}{∂y} + \frac{∂τ_{zx}}{∂z} +X=0\)
b) \(\frac{∂τ_{xy}}{∂x}+\frac{∂σ_y}{∂y}+\frac{∂τ_{zy}}{∂z}=0\)
c) \(\frac{∂τ_{xz}}{∂x} +\frac{∂τ_{yz}}{∂y} +\frac{∂σ_z}{∂z} +Z=0\)
d) \(\frac{∂σ_x}{∂x}+\frac{∂τ_{yx}}{∂y} +\frac{∂τ_{zx}}{∂z} = 0\)
View Answer
Explanation: The equilibrium equations in terms of total stresses formed by summing all forces on y-direction will include seepage force; the body forces will be equal to those due to gravity in respective directions.
∴ Y=0,
The equilibrium equation obtained by summing all forces on y-direction is,
\(\frac{∂τ_{xy}}{∂x} + \frac{∂σ_y}{∂y} +\frac{∂τ_{zy}}{∂z}+Y=0\)
Therefore, the equilibrium equations in terms of total stresses formed by summing all forces on x-direction is,
\(\frac{∂τ_{xy}}{∂x} + \frac{∂σ_y}{∂y} + \frac{∂τ_{zy}}{∂z}=0.\)
10. The equilibrium equations in terms of total stresses formed by summing all forces on z-direction is ________
a) \(\frac{∂σ_x}{∂x} + \frac{∂τ_{yx}}{∂y} + \frac{∂τ_{zx}}{∂z} +Z=0\)
b) \(\frac{∂τ_{xy}}{∂x}+\frac{∂σ_y}{∂y}+\frac{∂τ_{zy}}{∂z}=0\)
c) \(\frac{∂τ_{xz}}{∂x} +\frac{∂τ_{yz}}{∂y} +\frac{∂σ_z}{∂z} +γ=0\)
d) \(\frac{∂σ_x}{∂x}+\frac{∂τ_{yx}}{∂y} +\frac{∂τ_{zx}}{∂z} = 0\)
View Answer
Explanation: The equilibrium equations in terms of total stresses formed by summing all forces on z-direction will include seepage force; the body forces will be equal to those due to gravity in respective directions.
∴Z=γ,
The equilibrium equation obtained by summing all forces on z-direction is,
\(\frac{∂τ_{xz}}{∂x} +\frac{∂τ_{yz}}{∂y} +\frac{∂σ_z}{∂z} +Z=0\)
Therefore, the equilibrium equations in terms of total stresses formed by summing all forces on x-direction is,
\(\frac{∂τ_{xz}}{∂x}+\frac{∂τ_{yz}}{∂y} +\frac{∂σ_z}{∂z}+γ=0.\)
11. The normal stress in x-direction in terms of effective stress is given by __________
a) σx= σx’+γw(h-he)
b) σx= σx’*γw(h-he)
c) σx= σx’-γw(h-he)
d) σx= σx’
View Answer
Explanation: The total stress is equal to effective stress plus pore pressure. In x- direction, the normal stress is given by,
σx= σx’+u
u= γw(h-he)
where, h=total head at the point
he=elevation head
∴ σx= σx’+γw(h-he).
12. The normal stress in y-direction in terms of effective stress is given by __________
a) σy= σy’-γw(h-he)
b) σy= σy’+γw(h-he)
c) σy= σy’/γw(h-he)
d) σy= σy’*γw(h-he)
View Answer
Explanation: The total stress is equal to effective stress plus pore pressure. In y- direction, the normal stress is given by,
σy= σy’+u
u= γw(h-he)
where, h=total head at the point
he=elevation head
∴ σy= σy’+γw(h-he).
13. The normal stress in z-direction in terms of effective stress is given by __________
a) σz= γw(h-he)
b) σz= σz’
c) σz= σz’+γw(h-he)
d) σz= σz’-γw(h-he)
View Answer
Explanation: The total stress is equal to effective stress plus pore pressure. In x- direction, the normal stress is given by,
σz= σz’+u
u= γw(h-he)
where, h=total head at the point
he=elevation head
∴ σz= σz’+γw(h-he).
14. The partial differential of normal stress in x-direction in terms of effective stress is given by __________
a) \(\frac{∂σ_x{‘}}{∂x}\)
b) \(\frac{∂σ_x{‘}}{∂x}-γ_w \frac{∂h}{∂x}\)
c) \(\frac{∂σ_x{‘}}{∂x}+γ_w \frac{∂h}{∂x}\)
d) \(\frac{∂σ_x{‘}}{∂x}*γ_w \frac{∂h}{∂x}\)
View Answer
Explanation: Since, the normal stress in x-direction in terms of effective stress is given by,
σx= σx’+γw(h-he)
differentiating partially with respect to x,
\(\frac{∂σ_x}{∂x} = \frac{∂σ_x{‘}}{∂x} + γ_w \frac{∂(h-h_e)}{∂x}\)
But since \(\frac{∂h_e}{∂x}=0,\)
∴ \(\frac{∂σ_x}{∂x} = \frac{∂σ_x{‘}}{∂x+γ_w} \frac{∂h}{∂x}.\)
15. The partial differential of normal stress in y-direction in terms of effective stress is given by __________
a) \(\frac{∂σ_y{‘}}{∂y}\)
b) \(\frac{∂σ_y{‘}}{∂y}-γ_w \frac{∂h}{∂y}\)
c) \(\frac{∂σ_y{‘}}{∂y}+γ_w \frac{∂h}{∂y}\)
d) \(\frac{∂σ_y{‘}}{∂y}*γ_w \frac{∂h}{∂y}\)
View Answer
Explanation: Since, the normal stress in y-direction in terms of effective stress is given by,
σy= σy’+γw(h-he)
differentiating partially with respect to y,
\(\frac{∂σ_y}{∂y} = \frac{∂σ_y{‘}}{∂y} +γ_w \frac{∂(h-h_e)}{∂y}\)
But since \(\frac{∂h_e}{∂y}=0,\)
∴ \(\frac{∂σ_y}{∂y} = \frac{∂σ_y{‘}}{∂y}+γ_w \frac{∂h}{∂y}.\)
Sanfoundry Global Education & Learning Series – Soil Mechanics.
To practice all areas of Soil Mechanics, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
- Check Civil Engineering Books
- Practice Civil Engineering MCQs
- Apply for Civil Engineering Internship
- Check Geotechnical Engineering I Books
- Practice Geotechnical Engineering II MCQs
