This set of Soil Mechanics Multiple Choice Questions & Answers (MCQs) focuses on “Terzaghi’s Theory of One Dimensional Consolidation – 3”.
1. If v is velocity at the entry of the soil element of size dx, dz and width dy as shown in the figure. The quantity of water entering the element is ___________
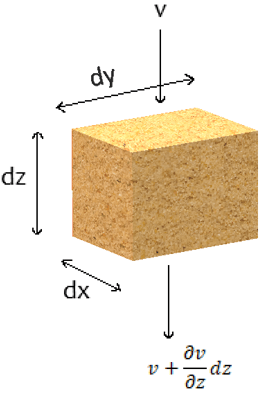
a) v
b) vdxdy
c) vdzdy
d) vdzdx
View Answer
Explanation: Since the quantity of water q is equal to velocity of flow time the area of cross-section through which it flows,
∴ q=v*A. The area of element is dxdy.
∴ The quantity of water entering the element is vdxdy.
2. If v is velocity at the entry of the soil element of size dx, dz and width dy as shown in the figure. The quantity of water leaving the element is ___________

a) v
b) vdxdy
c) \((v + \frac{∂v}{∂z}dz)dxdy\)
d) \((v + \frac{∂v}{∂z}dz)dxdz\)
View Answer
Explanation: Since the quantity of water q is equal to velocity of flow time the area of cross-section through which it flows,
∴ q=v*A. The area of element is dxdy. The velocity leaving the element is \((v + \frac{∂v}{∂z}dz).\) Therefore, the quantity of water leaving the element is \((v + \frac{∂v}{∂z}dz)dxdy.\)
3. If v is velocity at the entry of the soil element of size dx, dz and width dy as shown in the figure. The net quantity of water squeezed out of the element per unit time is ___________

a) ∆q=v
b) ∆q=vdxdy
c) \(∆q= \frac{∂v}{∂z}vdzdy\)
d) \(∆q=\frac{∂v}{∂z}dxdydz\)
View Answer
Explanation: The net quantity of water squeezed out of the element per unit time is given by,
\(∆q=q_{out}-q_{in}=(v + \frac{∂v}{∂z}dz)dxdy- vdxdy\)
∴ \(∆q=\frac{∂v}{∂zdxdydz}. \)
4. Decrease in the volume of the soil is equal to _________
a) volume of water squeeze out
b) volume of water entering the soil element
c) volume of water leaving the soil element
d) volume of soil in wet state
View Answer
Explanation: Since the water occupies the voids between the soil particles and when the force is applied, the water is squeezed out and there is decrease in volume of soil. Therefore, decrease in the volume of the soil is equal to the volume of water squeeze out.
5. The decrease in volume is given by the equation ___________
a) ∆v=-V0 ∆σ’
b) ∆v=-av V0 ∆σ’
c) ∆v=-mv ∆σ’
d) ∆v=-mv V0 ∆σ’
View Answer
Explanation: The decrease in the volume of the soil is equal to the volume of water squeeze out. Thus, the decrease in volume is given by the equation,
\(\)∆v=-mv V0 ∆σ’ where the negative sign indicates the decrease in volume.
6. The change of volume per unit time is __________
a) \(\frac{∂∆V}{∂z}=-V_0 ∆σ’\)
b) \(\frac{∂∆V}{∂z}=-a_v V_0 ∆σ’\)
c) \(\frac{∂∆V}{∂z}=-m_v \frac{∂∆σ’}{∂t}\)
d) \(\frac{∂∆V}{∂z}=-m_v dxdydz \frac{∂∆σ’}{∂t}\)
View Answer
Explanation: Since the decrease in volume is given by the equation,
∆v=-mv V0 ∆σ’ where V0=dxdydz,
differentiating the equation, we get,
\(\frac{∂∆V}{∂z}=-m_v dxdydz \frac{∂∆σ’}{∂t}\) where, mv is the coefficient of volume change.
7. The partial differentiation of velocity of water in soil element with respect to depth z in terms of coefficient of volume change is given by ____________
a) \(\frac{∂v}{∂z}=m_v \frac{∂^2 \overline{u}}{∂t^2}\)
b) \(\frac{∂v}{∂z}=m_v \frac{\overline{u}}{∂t^2}\)
c) \(\frac{∂v}{∂z}=\frac{∂^2 \overline{u}}{∂t^2}\)
d) \(\frac{∂v}{∂z}=m_v \frac{∂\overline{u}}{∂t}\)
View Answer
Explanation: From the volume of water squeezed out, ∆q=\(\frac{∂v}{∂z}\) dxdydz and change of volume per unit time, \(\frac{∂∆V}{∂z}=-m_v dxdydz \frac{∂∆σ’}{∂t}\)
we get, \(\frac{∂v}{∂z}=-m_v \frac{∂∆σ’}{∂t}\) —————–(1)
since, ∆σ=∆σ’+u, partally differentiating it with respect to time t,
\(\frac{∂∆σ’}{∂t}=-\frac{∂\overline{u}}{∂t}\) ————————(2)
∴ from (1) and (2),
\(\frac{∂v}{∂z}=m_v \frac{∂\overline{u}}{∂t}.\)
8. The term \(\frac{∂\overline{u}}{∂t}\) in terms of coefficient of volume change and coefficient of permeability is given by ____________
a) \(\frac{∂\overline{u}}{∂t}=\frac{k}{m_v γ_w} \frac{∂\overline{u}}{∂z}\)
b) \( \frac{∂\overline{u}}{∂t}=\frac{k}{m_v γ_w} \frac{∂\overline{u}}{∂z}\)
c) \( \frac{∂\overline{u}}{∂t}=\frac{k}{m_v γ_w} \frac{∂^2\overline{u}}{∂z^2}\)
d) \( \frac{∂\overline{u}}{∂t}=\frac{k}{m_v γ_w} \frac{∂\overline{u}}{∂z}\)
View Answer
Explanation: The decrease in volume is given by,
∆v=-mv V0 ∆σ’—————–(1)
also \(\frac{∂v}{∂z}=m_v \frac{∂\overline{u}}{∂t}\) ——————————-(2)
∴ from (1) and (2), we get,
\(\frac{∂\overline{u}}{∂t}=\frac{k}{m_v γ_w}\frac{∂^2 \overline{u}}{∂z^2}.\)
9. The coefficient of consolidation is given by ___________
a) \(C_v=\frac{q}{m_v γ_w}\)
b) \(C_v=\frac{1}{m_v γ_w}\)
c) \(C_v=\frac{k}{m_v} \)
d) \(C_v=\frac{k}{m_v γ_w}\)
View Answer
Explanation: The coefficient of consolidation is given by,
\(C_v=\frac{k}{m_v γ_w}\)
where, k=coefficient of permeability
mv=coefficient of volume change
γw=unit weight of water.
10. The coefficient of consolidation in terms of voids ratio e and coefficient of compressibility is ____________
a) \(C_v=\frac{k(1+e_0)}{a_v γ_w}\)
b) \(C_v=\frac{k(1-e_0)}{a_v γ_w}\)
c) \(C_v=\frac{k(e_0)}{a_v γ_w}\)
d) \(C_v=\frac{(1+e_0)}{a_v γ_w}\)
View Answer
Explanation: Since we know the coefficient of volume change \(m_v=\frac{a_v}{1+e_0} \)
and the coefficient of consolidation is given by,
\(C_v=\frac{k}{m_v γ_w}.\) Therefore, combining the two equations, we get,
\(C_v=\frac{k(1+e_0)}{a_v γ_w}.\)
11. The term coefficient of consolidation Cv used in equation is adopted to indicate the effect of permeability only.
a) True
b) False
View Answer
Explanation: The term coefficient of consolidation Cv used in equation is adopted to indicate the combined effects of the permeability and the compressibility of the soil on the rate of volume change.
12. The units of Cv is ___________
a) cm/s
b) cm
c) s
d) cm2/s
View Answer
Explanation: The coefficient of consolidation Cv is given by,
\(C_v=\frac{k}{m_v γ_w}\)
where, k is in cm/s
mv in cm2/kN
and γw in kN/cm3.
combining the units of these in the formula,
The units of Cv is cm2/s.
Sanfoundry Global Education & Learning Series – Soil Mechanics.
To practice all areas of Soil Mechanics, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
- Practice Civil Engineering MCQs
- Apply for Civil Engineering Internship
- Check Civil Engineering Books
- Practice Geotechnical Engineering II MCQs
- Check Geotechnical Engineering I Books
