This set of Soil Mechanics Question Paper focuses on “Secondary Consolidation and Three Dimensional Consolidation – 2”.
1. The three dimensional consolidation involves _____________
a) only horizontal flow and strain
b) only vertical flow and strain
c) both horizontal as well as vertical flows and strains
d) only radial flow and strain
View Answer
Explanation: In actual problems of surface loadings, the pore pressure varies in both horizontal and vertical direction. Therefore, in three dimensional consolidation, it involves both horizontal as well as vertical flows and strains.
2. The theory of the primary design of sand drains based upon the extension of Terzaghi’s basic work was largely developed by ___________
a) Darcy
b) Skempton
c) Taylor
d) Barron
View Answer
Explanation: The theory of the primary design of sand drains based upon the extension of Terzaghi’s basic work was largely developed by Barron during 1940- 1942. Darcy worked on the permeability of soils.
3. In 1935, solved the differential equation of consolidation by radial flow to a well.
a) Rendulic
b) Skempton
c) Taylor
d) Darcy
View Answer
Explanation: Prior to Barron’s work, Rendulic in 1935 solved the differential equation of consolidation by radial flow to a well. Skempton is known for his pore pressure parameters A and B.
4. ______________ also worked independently on the problem of sand drains and published his results in 1942.
a) Carillo
b) Skempton
c) Taylor
d) Rendulic
View Answer
Explanation: Rendulic in 1935 solved the differential equation of consolidation by radial flow to a well. Carillo also worked independently on the problem of sand drains and published his results in 1942.
5. In three dimension consolidation equation soil is assumed to be ______________
a) partially saturated
b) dry
c) completely saturated
d) both dry and partially saturated
View Answer
Explanation: When the soil is fully saturated, then there are no air voids present in the soil and thus making the calculations easier. So, in three dimension consolidation equation soil is assumed to be completely saturated.
6. In three dimension consolidation equation soil is assumed to be ____________
a) homogenous
b) non-homogenous
c) anisotropic
d) heterogeneous
View Answer
Explanation: In nature, soils are non-homogeneous media, and anisotropic in general. This means that their properties vary within relatively short distances in the vertical and horizontal directions. For the simplicity in solving the equations the soil is considered to be homogenous.
7. In three dimension consolidation equation, the pressure increment is ____________
a) applied instantaneously
b) applied periodically
c) applied intermittently
d) not applied at all
View Answer
Explanation: In three dimension consolidation equation, it is made an assumption that, the pressure increment ∆σ’ is applied instantaneously so that t is independent of time.
8. Considering a parallelepiped for three dimensional consolidation, the volume of water flowing into parallelepiped is __________
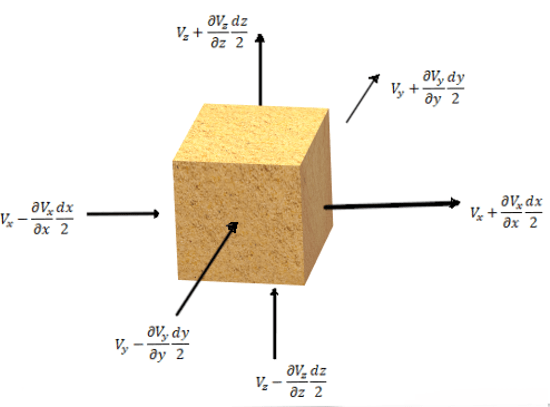
a) \(q_{in}=(V_x-\frac{∂V_x}{∂x} \frac{dx}{2})dydz-(V_y-\frac{∂V_y}{∂y} \frac{dy}{2})dxdz-(V_z-\frac{∂V_z}{∂z} \frac{dz}{2})dxdy\)
b) \(q_{in}=(V_x-\frac{∂V_x}{∂x} \frac{dx}{2})dydz+(V_y-\frac{∂V_y}{∂y} \frac{dy}{2})dxdz+(V_z-\frac{∂V_z}{∂z} \frac{dz}{2})dxdy\)
c) \(q_{in}=(V_x-\frac{∂V_x}{∂x} \frac{dx}{2})dydz+(V_y-\frac{∂V_y}{∂y} \frac{dy}{2})dxdz-(V_z-\frac{∂V_z}{∂z} \frac{dz}{2})dxdy\)
d) \(q_{in}=(V_x-\frac{∂V_x}{∂x} \frac{dx}{2})dydz-(V_y-\frac{∂V_y}{∂y} \frac{dy}{2})dxdz+(V_z-\frac{∂V_z}{∂z} \frac{dz}{2})dxdy\)
View Answer
Explanation: Since the quantity of water q is equal to velocity of flow time the area of cross-section through which it flows,
∴ q=v*A.
Therefore, for side of the face in which the water enters is given by,
\(q_{in}=(V_x-\frac{∂V_x}{∂x} \frac{dx}{2})dydz+(V_y-\frac{∂V_y}{∂y} \frac{dy}{2})dxdz+(V_z-\frac{∂V_z}{∂z} \frac{dz}{2})dxdy.\)
9. Considering a parallelepiped for three dimensional consolidation, the volume of water flowing out of parallelepiped is ______________

a) \(q_{out}=(V_x+\frac{∂V_x}{∂x} \frac{dx}{2})dydz+(V_y+\frac{∂V_y}{∂y} \frac{dy}{2})dxdz+(V_z+\frac{∂V_z}{∂z} \frac{dz}{2})dxdy\)
b) \(q_{out}=(V_x+\frac{∂V_x}{∂x} \frac{dx}{2})dydz-(V_z+\frac{∂V_z}{∂z} \frac{dz}{2})dxdy\)
c) \(q_{out}=(V_x-\frac{∂V_x}{∂x} \frac{dx}{2})dydz\)
d) \(q_{out}=(V_x-\frac{∂V_x}{∂x} \frac{dx}{2})dydz-(V_y-\frac{∂V_y}{∂y} \frac{dy}{2})dxdz+(V_z-\frac{∂V_z}{∂z} \frac{dz}{2})dxdy\)
View Answer
Explanation: Since the quantity of water q is equal to velocity of flow time the area of cross-section through which it flows,
∴q=v*A.
Therefore, for side of the face in which the water leaves is given by,
\(q_{out}=(V_x+\frac{∂V_x}{∂x} \frac{dx}{2})dydz+(V_y+\frac{∂V_y}{∂y} \frac{dy}{2})dxdz+(V_z+\frac{∂V_z}{∂z} \frac{dz}{2})dxdy.\)
10. The volume of water squeezed out from the parallelepiped is _______________

a) \(dq=(\frac{∂V_x}{∂x}+\frac{∂V_y}{∂y}+\frac{∂V_z}{∂z})dxdydz \)
b) \(dq=(V_x+\frac{∂V_x}{∂x} \frac{dx}{2})dydz-(V_z+\frac{∂V_z}{∂z} \frac{dz}{2})dxdy \)
c) \(dq=(V_x-\frac{∂V_x}{∂x} \frac{dx}{2})dydz \)
d) \(dq=(V_x-\frac{∂V_x}{∂x} \frac{dx}{2})dydz-(V_y-\frac{∂V_y}{∂y} \frac{dy}{2})dxdz+(V_z-\frac{∂V_z}{∂z} \frac{dz}{2})dxdy \)
View Answer
Explanation: The volume of water that is squeezed out is given by,
dq=q
∴ \(dq=(V_x+\frac{∂V_x}{∂x} \frac{dx}{2})dydz+(V_y+\frac{∂V_y}{∂y} \frac{dy}{2})dxdz+(V_z+\frac{∂V_z}{∂z} \frac{dz}{2})dxdy- \)
\([(V_x-\frac{∂V_x}{∂x} \frac{dx}{2})dydz+(V_y-\frac{∂V_y}{∂y} \frac{dy}{2})dxdz+(V_z-\frac{∂V_z}{∂z}\frac{dz}{2})dxdy]. \)
∴ \(dq=(\frac{∂V_x}{∂x}+\frac{∂V_y}{∂y}+\frac{∂V_z}{∂z})dxdydz. \)
Sanfoundry Global Education & Learning Series – Soil Mechanics.
To practice all questions papers on Soil Mechanics, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
- Practice Civil Engineering MCQs
- Check Geotechnical Engineering I Books
- Practice Geotechnical Engineering II MCQs
- Apply for Civil Engineering Internship
- Check Civil Engineering Books
