This set of Soil Mechanics Multiple Choice Questions & Answers (MCQs) focuses on “Stress Distribution – Vertical Pressure – 2”.
1. For maximum vertical stress, the shear stress is _________ if the load is 30 kN and r=4m.
a) 0.4356 kN/m2
b) 0.1359 kN/m2
c) 0.1518 kN/m2
d) 0.3625 kN/m2
View Answer
Explanation: Given,
r=4m
Q=30 kN
\(τ_{rz}=\frac{0.0725Q}{r^2} \)
\(τ_{rz}=\frac{0.0725*30}{4^2} \)
∴ τrz=0.1359kN/m2.
2. What will be the intensity of shear stress at a depth of 4m and at a radial distance of 1m from concentrated load of 20 kN?
a) 0.4356 kN/m2
b) 0.244 kN/m2
c) 0.652 kN/m2
d) 0.128 kN/m2
View Answer
Explanation: Given,
Z=4m
Q=20 kN
r=1
The Boussinesq’s shear stress τrz is given by,
\(τ_{rz}=\frac{3Qr}{2πz^3}\left[\frac{1}{1+(\frac{r}{z})^2}\right]^{\frac{5}{2}} \)
∴ \(τ_{rz}=\frac{3*20*1}{2π4^3}\left[\frac{1}{1+(\frac{1}{4})^2}\right]^{\frac{5}{2}} \)
∴ τrz=0.128 kN/m2.
3. If r/z ratio is 2 and load of 20 kN is acting at a point, then the vertical pressure at a depth 6m is ____________
a) 0.4356 kN/m2
b) 0.244 kN/m2
c) 0.1518 kN/m2
d) 4.72*10-3 kN/m2
View Answer
Explanation: Given,
r/z=2
Q=20 kN
Z=6m
\(σ_z=\frac{0.0085Q}{z^2} \)
\(σ_z=\frac{0.0085*20}{6^2} \)
σz=4.72*10-3 kN/m2.
4. The Boussinesq influence factor for r/z ratio equal to 1 is given by ____________
a) 0.3840
b) 0.5465
c) 0.0844
d) 0.2312
View Answer
Explanation: Given,
r/z=1
The Boussinesq influence factor is given by,
\(K_B=\frac{3}{2π} \left[\frac{1}{1+(\frac{r}{z})^2}\right]^{\frac{5}{2}} \)
\(K_B=\frac{3}{2π} \left[\frac{1}{1+1^2}\right]^{\frac{5}{2}} \)
KB=0.0844.
5. When the maximum vertical stress is 0.235 kN/m2 at a radial distance of 4m from the point load is __________ kN.
a) 42.34
b) 10.56
c) 20.76
d) 30.65
View Answer
Explanation: Given,
(σz)max=0.235 kN/m2
r=4m
since the maximum vertical stress is
\((σ_z)_{max}=\frac{0.0888Q}{r^2} \)
∴ \(Q=\frac{(σ_z)_{max}r^2}{0.0888} \)
∴ \(Q=\frac{0.235*4^2}{0.0888} \)
Q=42.34 kN.
6. The Boussinesq’s vertical pressure σz under a uniformly loaded circular area is given by ________
a) \(σ_z=q\left[1-\left[\frac{1}{1+(\frac{a}{z})^2}\right]^{\frac{3}{2}}\right] \)
b) \(σ_z=q\left[1+\left[\frac{1}{1+(\frac{a}{z})^2}\right]^{\frac{3}{2}}\right] \)
c) \(σ_z=q\left[\frac{1}{1+(\frac{a}{z})^2}\right]^{\frac{3}{2}} \)
d) \(σ_z=q\left[1-\left[\frac{1}{1+(\frac{a}{z})^2}\right]^{\frac{5}{2}}\right] \)
View Answer
Explanation: The Boussinesq’s vertical pressure σz under a uniformly loaded circular area is given by,
\(σ_z=q\left[1-\left[\frac{1}{1+(\frac{a}{z})^2}\right]^{\frac{3}{2}}\right] \)
where, q=load intensity per unit area
a=radius of circle
z= depth of point.
7. The Boussinesq influence factor for uniformly distributed circular area is given by ____________
a) \(K_B= \left[1-\left[\frac{1}{1+(\frac{a}{z})^2}\right]^{\frac{3}{2}}\right] \)
b) \(K_B= \left[1+\left[\frac{1}{1+(\frac{a}{z})^2}\right]^{\frac{3}{2}}\right] \)
c) \(K_B= \left[\frac{1}{1+(\frac{a}{z})^2}\right]^{\frac{3}{2}} \)
d) \(K_B= q\left[1-\left[\frac{1}{1+(\frac{a}{z})^2}\right]^{\frac{5}{2}}\right] \)
View Answer
Explanation: The Boussinesq influence factor for uniformly distributed circular area is given by,
\(K_B= \left[1-\left[\frac{1}{1+(\frac{a}{z})^2}\right]^{\frac{3}{2}}\right] \)
where the KB= Boussinesq influence factor which is a function of r/z ratio which is a dimensionless factor.
8. If θ is the apex angle which the line joining the apex makes with the outer edge of the loading of a circular area, then the Boussinesq’s vertical pressure σz under a uniformly loaded circular area is given by ______________
a) σz=q[1-sin3θ]
b) σz=q[1-cos3θ]
c) σz=q[1-tan3θ]
d) σz=q[1-cos2θ]
View Answer
Explanation: The Boussinesq’s vertical pressure σ_z under a uniformly loaded circular area is given by,
\(σ_z=q\left[1-\left[\frac{1}{1+(\frac{a}{z})^2}\right]^{\frac{3}{2}}\right]. \) If θ is the apex angle which the line joining the apex makes with the outer edge of the loading of a circular area, then the term,
\(\left[\frac{1}{1+(\frac{a}{z})^2}\right]^{\frac{3}{2}} = cos^3 θ\)
∴ σz=q[1-cos3θ].
9. The Boussinesq’s vertical pressure σz due to line load is given by ________
a) \(σ_z=\frac{5q’}{πz}\frac{1}{[1+\frac{x}{z}^2 ]^2} \)
b) \(σ_z=\frac{3q’}{πz}\frac{1}{[1+(\frac{x}{z})^2 ]^2} \)
c) \(σ_z=\frac{2q’}{πz}\frac{1}{[1+(\frac{x}{z})^2 ]^2} \)
d) \(σ_z=\frac{2q’}{z}\frac{1}{[1+⌊\frac{x}{z}⌋^2 ]^2} \)
View Answer
Explanation: The Boussinesq’s vertical pressure σz due to line load is given by,
\(σ_z=\frac{2q’}{πz}\frac{1}{[1+(\frac{x}{z})^2 ]^2} \)
Where q’=line load intensity per unit length
X=horizontal distance from line load
Z= depth of point.
10. The Boussinesq’s vertical pressure σz due to line load at a point situated vertically below the line load is given by ________
a) \(σ_z=\frac{2q’}{πz}\)
b) \(σ_z=\frac{3q’}{πz}\)
c) \(σ_z=\frac{2q’}{πz}\frac{1}{[1+(z)^2 ]^2} \)
d) \(σ_z=\frac{2q’}{z}\)
View Answer
Explanation: The Boussinesq’s vertical pressure σz due to line load is given by,
\(σ_z=\frac{2q’}{πz}\frac{1}{[1+(\frac{x}{z})^2 ]^2} \) at a point situated vertically below the line load implies x=0
∴ \(σ_z=\frac{2q’}{πz}\frac{1}{[1+(\frac{0}{z})^2 ]^2} \)
∴ \(σ_z=\frac{2q’}{πz}.\)
11. If θ is the angle subtended by the edges of the strip load, then the Boussinesq’s vertical pressure σz due to strip load is given by ________
a) \(σ_z=\frac{q}{π}(θ+sinθ)\)
b) \(σ_z=\frac{q}{π}(θ-sinθ)\)
c) \(σ_z=\frac{q}{π}(sinθ)\)
d) \(σ_z=\frac{q}{π} θ\)
View Answer
Explanation:
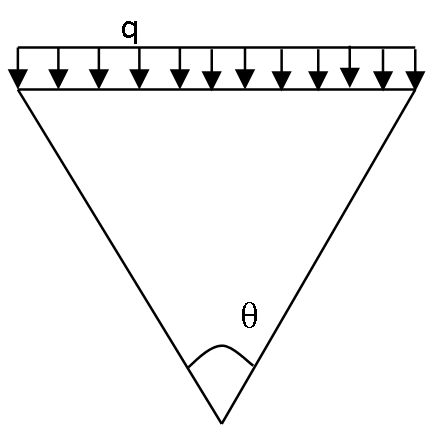
The vertical pressure due to elementary line load is given by,
\(∆σ_z=\frac{2q’}{πz}\frac{1}{[1+(\frac{0}{z})^2 ]^2} \)
When θ is the angle subtended by the edges of the strip load, the Boussinesq’s vertical pressure σz due to strip load is given by \(σ_z=\frac{q}{π}(θ+sinθ).\)
Sanfoundry Global Education & Learning Series – Soil Mechanics.
To practice all areas of Soil Mechanics, here is complete set of 1000+ Multiple Choice Questions and Answers.
