Soil Mechanics Questions and Answers – Elasticity – Boundary Condition Equations

This set of Soil Mechanics Multiple Choice Questions & Answers (MCQs) focuses on “Elasticity – Boundary Condition Equations”.

1. The boundary condition equation for X, where X is the component of the surface force in x-direction per unit area is ___________
a) X = σ_y m+τ_yz n+τ_xy l
b) X = σ_z n+τ_zx l+τ_zy m
c) X = σ_x l+τ_yx m+τ_zx n
d) X = σ_y l+τ_yx m+τ_zx n
View Answer

Answer: c
Explanation: Let the area of ABC=ds.

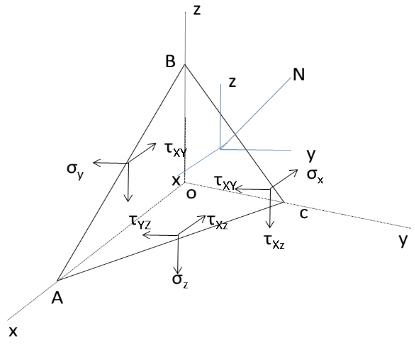
area OBC=ds cos(N,x)=ds.l
area OAB=ds cos(N,y)=ds.m
area OAC=ds cos(N,z)=ds.n
Resolving all the forces in x-direction and equating them to zero, we get,
X = σ_x l+τ_yx m+τ_zx n.

2. The boundary condition equation for Y, where Y is the component of the surface force in y-direction per unit area is ___________
a) Y = σ_y m+τ_yz n+τ_xy l
b) Y = σ_z n+τ_zx l+τ_zy m
c) Y = σ_x l+τ_yx m+τ_zx n
d) Y = σ_y l+τ_yx m+τ_zx n
View Answer

Answer: a
Explanation: Let the area of ABC=ds.

area OBC=ds cos(N,x)=ds.l
area OAB=ds cos(N,y)=ds.m
area OAC=ds cos(N,z)=ds.n
Resolving all the forces in y-direction and equating them to zero, we get,
Y = σ_y m+τ_yz n+τ_xy l.

3. The boundary condition equation for Z, where Z is the component of the surface force in z-direction per unit area is ___________
a) Z = σ_y m+τ_yz n+τ_xy l
b) Z = σ_z n+τ_zx l+τ_zy m
c) Z = σ_x l+τ_yx m+τ_zx n
d) Z = σ_y l+τ_yx m+τ_zx n
View Answer

Answer: b
Explanation: Let the area of ABC=ds.

area OBC=ds cos(N,x)=ds.l
area OAB=ds cos(N,y)=ds.m
area OAC=ds cos(N,z)=ds.n
Resolving all the forces in z-direction and equating them to zero, we get,
Z = σ_z n+τ_zx l+τ_zy m.

4. The matrix form of the boundary condition equations is _____________
a) \(\begin{bmatrix}
\overline{X}\\
\overline{Y}\\
\overline{Z}
\end{bmatrix} =
\begin{bmatrix}
σ_{xx} & τ_{xy} & τ_{xz} \\
τ_{yx} & σ_{yy} & τ_{yz} \\
τ_{zx} & τ_{zy} & σ_{zz}
\end{bmatrix}
\begin{bmatrix}
l \\
m \\
n
\end{bmatrix} \)
b) \(\begin{bmatrix}
\overline{X}\\
\overline{Y}\\
\overline{Z}
\end{bmatrix} =
\begin{bmatrix}
σ_{zz} & τ_{xy} & τ_{xz} \\
τ_{yx} & σ_{yy} & τ_{yz} \\
τ_{zx} & τ_{zy} & σ_{xx}
\end{bmatrix}
\begin{bmatrix}
l \\
m \\
n
\end{bmatrix} \)
c) \(\begin{bmatrix}
\overline{X}\\
\overline{Y}\\
\overline{Z}
\end{bmatrix} =
\begin{bmatrix}
σ_{xx} & τ_{zz} & τ_{xz} \\
τ_{yx} & σ_{yy} & τ_{yz} \\
τ_{zx} & τ_{zy} & σ_{zz}
\end{bmatrix}
\begin{bmatrix}
l \\
m \\
n
\end{bmatrix} \)
d) \(\begin{bmatrix}
\overline{X}\\
\overline{Y}\\
\overline{Z}
\end{bmatrix} =
\begin{bmatrix}
σ_{xx} & τ_{yy} & τ_{xz} \\
τ_{yx} & σ_{yy} & τ_{yz} \\
τ_{zx} & τ_{yy} & σ_{zz}
\end{bmatrix}
\begin{bmatrix}
l \\
m \\
n
\end{bmatrix} \)
View Answer

5. The partial differential of normal stress in y-direction in terms of effective stress is given by __________
a) \(\frac{∂σ_z{‘}}{∂z}\)
b) \(\frac{∂σ_z{‘}}{∂z}-γ_w\frac{∂h}{∂z}\)
c) \(\frac{∂σ_z{‘}}{∂z}+γ_w\frac{∂h}{∂z}\)
d) \(\frac{∂σ_z{‘}}{∂z}*γ_w\frac{∂h}{∂z}\)
View Answer

6. The equilibrium equation in X-direction in terms of effected stress for a saturated soil body is given by __________
a) \(\frac{∂σ_x{‘}}{∂x}+\frac{∂τ_{yx}}{∂y}=0\)
b) \(\frac{∂τ_{xy}}{∂x}+\frac{∂σ_y{‘}}{∂y}+\frac{∂τ_{zy}}{∂z}+γ_w \frac{∂h}{∂x}=0\)
c) \(\frac{∂τ_{xz}}{∂x}+\frac{∂τ_{yz}}{∂y}+\frac{∂σ_z{‘}}{∂z}+γ_w \frac{∂h}{∂x}=0\)
d) \(\frac{∂σ_x{‘}}{∂x}+\frac{∂τ_{yx}}{∂y}+\frac{∂τ_{zx}}{∂z}+γ_w \frac{∂h}{∂x}=0\)
View Answer

7. The equilibrium equation in Y-direction in terms of effected stress for a saturated soil body is given by __________
a) \(\frac{∂σ_x{‘}}{∂x}+\frac{∂τ_{yx}}{∂y}+\frac{∂τ_{zx}}{∂z}+X=0\)
b) \(\frac{∂τ_{xy}}{∂x}+\frac{∂σ_y{‘}}{∂y}+\frac{∂τ_{zy}}{∂z}+γ_w \frac{∂h}{∂y}=0\)
c) \(\frac{∂τ_{xz}}{∂x}+\frac{∂τ_{yz}}{∂y}+\frac{∂σ_z{‘}}{∂z}+Z=0\)
d) \(\frac{∂σ_x{‘}}{∂x}+\frac{∂τ_{yx}}{∂y}+\frac{∂τ_{zx}}{∂z}=0\)
View Answer

8. The equilibrium equation in Z-direction in terms of effected stress for a saturated soil body is given by __________
a) \(\frac{∂σ_x{‘}}{∂x}+\frac{∂τ_{yx}}{∂y}+\frac{∂τ_{zx}}{∂z}++γ_w \frac{∂h}{∂z}=0\)
b) \(\frac{∂τ_{xy}}{∂x}+\frac{∂σ_y{‘}}{∂y}+\frac{∂τ_{zy}}{∂z}+γ_w \frac{∂h}{∂z}=0\)
c) \(\frac{∂τ_{xz}}{∂x}+\frac{∂τ_{yz}}{∂y}+\frac{∂σ_z{‘}}{∂z}+γ’+γ_w \frac{∂h}{∂z}=0\)
d) \(\frac{∂σ_x{‘}}{∂x}+\frac{∂τ_{yx}}{∂y}+\frac{∂τ_{zx}}{∂z}=0\)
View Answer

Sanfoundry Global Education & Learning Series – Soil Mechanics.

To practice all areas of Soil Mechanics, here is complete set of 1000+ Multiple Choice Questions and Answers.

If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]