This set of Soil Mechanics Multiple Choice Questions & Answers (MCQs) focuses on “Poiseuille’s Law”.
1. For flow of water in tube, the velocity at surface is ___________
a) zero
b) equal to velocity at 1/3 of diameter
c) equal to velocity at 1/2 of diameter
d) equal to velocity at centre
View Answer
Explanation: The surface of the tube is wet forming a very thin layer of water that is immobile due to molecular attraction. So the velocity at the surface is zero.
2. In Poiseuille’s law of flow, the variation of the velocity is given by _______
a) v = \(\frac{hγ_w}{4ηL}(r^2-R^2)\)
b) v = \(\frac{hγ_w}{14ηL}(R^2-r^2)\)
c) v = \(\frac{hγ_w}{4ηL}(R^2-r^2)\)
d) v = \(\frac{hγ_w}{8ηL}(R^2-r^2)\)
View Answer
Explanation: Consider a capillary tube of length L and radius R.
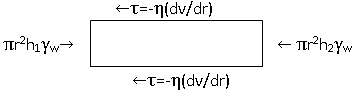
In equilibrium the sum of the forces is zero,
πr2h1γw– πr2h1γw-τ(2πrL)=0
on simplification, \(dv=-\frac{hγ_w}{2ηL}rdr\)
on integration,
\(v =- \frac{hγ_w}{4ηL}r^2 + C \,where\, C=\frac{hγ_w}{4ηL} R^2\)
∴ \(v = \frac{hγ_w}{4ηL}(R^2-r^2).\)
3. The velocity of flow of water at the centre of tube is _______ when the head is 0.1m, η=8.9*10-3 dynes-s/cm2, γw=1 g/cm3, the length is 10m and the diameter is 20cm.
a) 20 cm/s
b) 22 cm/s
c) 28 cm/s
d) 30 cm/s
View Answer
Explanation: Given,
h=0.1m
η=8.9*10-3 dynes-s/cm2
γw=1 g/cm3
L= 10m
d= 20cm.
Since \(v = \frac{hγ_w}{4ηL}(R^2-r^2)\)
\(v = \frac{10*1}{4*8.9*10^{-3}*1000}(10^2-0^2)\)
v=28 cm/s.
4. The quantity of water flowing in thin cylindrical sheet of thickness dr is ____________
a) \(dq=\frac{hγ_w}{4ηL}(R^2-r^2)2πrdr\)
b) \(dq=\frac{hγ_w}{4ηL}(R^2-r^2)4πrdr\)
c) \(dq=\frac{hγ_w}{4ηL}(R^2-r^2)8πrdr\)
d) \(dq=\frac{hγ_w}{4ηL}(R^2-r^2)12πrdr\)
View Answer
Explanation: Consider a capillary tube of length L and radius R.
dq=(2πrdr)v
substituting for velocity,
\(dq=(2πrdr)*\frac{hγ_w}{4ηL}(R^2-r^2)\)
\( ∴ dq=\frac{hγ_w}{4ηL}(R^2-r^2)2πrdr.\)
5. The total quantity of water flowing through the capillary tube is given by _________
a) \(q=\frac{hγ_w}{4ηL} R^2 \)
b) \(q=\frac{hγ_w}{4ηL} R^4\)
c) \(q=\frac{hγ_w}{8ηL} R^2\)
d) \(q=\frac{hγ_w}{8ηL} πR^4\)
View Answer
Explanation: The total quantity of flow is obtained by integrating with the limits 0 to R in the differential discharge.
\(dq=\frac{hγ_w}{4ηL} (R^2-r^2)2πrdr\)
\(q=\frac{hγ_w}{4ηL}\int_0^R (R^2-r^2)2πrdr\)
\( ∴ q=\frac{hγ_w}{8ηL} πR^4\)
6. The total quantity of water with respect to the hydraulic gradient flowing through the capillary tube is given by _________
a) \( q=\frac{hiγ_w}{4ηL} R^2 \)
b) \( q=\frac{hγ_w}{4ηL} R^4/i\)
c) \( q=\frac{iγ_w}{8η} π R^2\)
d) \( q=\frac{iγ_w}{8η} πR^4\)
View Answer
Explanation: The hydraulic gradient i is the head loss divided by the length travelled,
i=h/L
\( ∴ q=\frac{hγ_w}{8ηL} πR^4 = \frac{iγ_w}{8η}πR4.\)
7. The average velocity of the tube of area a is given by _________
a) \(v_{av}=\frac{iγ_w}{8ηπ}a \)
b) \(v_{av}=\frac{\frac{iγ_w}{8ηπ}}{a}\)
c) \(v_{av}=\frac{iγ_w}{2ηπ}a\)
d) \(v_{av}=\frac{\frac{iγ_w}{4ηπ}}{a}\)
View Answer
Explanation: The average velocity is given by,
Vav=q/a
Vav=q/πr2
Substituting for q,
∴ \(v_{av}=\frac{iγ_w}{8ηπ}a. \)
8. The hydraulic radius RH is the ratio of the area of the tube to its volume.
a) True
b) False
View Answer
Explanation: The hydraulic radius RH is defined as the ratio of the area of the tube to the wetted perimeter. It is used to generally designate the velocity of flow in engineering hydraulics.
9. The hydraulic radius RH of circular tube is given by ________
a) RH=R/4
b) RH=R/6
c) RH=R/2
d) RH=R/12
View Answer
Explanation: The hydraulic radius RH is defined as the ratio of the area of the tube to the wetted perimeter.
∴ RH=A/P=πR2/2πR
∴ RH=R/2.
10. The hydraulic radius RH is related with the voids ratio as ________
a) RH=Vs/eAs
b) RH=eVsAs
c) RH=e/AsVs
d) RH=eVs/As
View Answer
Explanation: The hydraulic radius RH is given by,
RH=A/P=AL/PL
AL=eVs
PL= As
∴ RH=eVs/As.
11. The quantity of flow for circular tube with respect to the hydraulic radius is given by ________
a) \(q=\frac{1}{2}\frac{γ_w R_H^2}{η} \)
b) \(q=\frac{1}{2}\frac{γ_w R_H^2}{η}ia\)
c) \(q=\frac{1}{2}\frac{γ_w R_H^2}{η}i\)
d) \(q=\frac{1}{2}\frac{γ_w R_H^2}{η}a \)
View Answer
Explanation: The quantity of flow for the capillary tube of any geometrical shape is given by,
\(q=C_S \frac{γ_w R_H^2}{η}ia\), where Cs is the shape constant.
For circular tube Cs=1/2
\( ∴ q=\frac{1}{2}\frac{γ_w R_H^2}{η}ia.\)
12. The relationship between the quantity of flow with respect to the hydraulic radius and the voids ratio is given by ________
a) \(q=\frac{γ_w R_H^2}{η}\frac{e}{1+e}iA\)
b) \(=C_S\frac{γ_w R_H^2}{η}\frac{e}{1+e}\)
c) \(=C_S\frac{γ_w R_H^2}{η}iA\)
d) \(=C_S\frac{γ_w R_H^2}{η}\frac{e}{1+e}iA\)
View Answer
Explanation: Let the total cross-section of the soil be A and the porosity be n,
∴ a=nA
∴ \(q=\frac{1}{2}\frac{γ_w R_H^2}{η}ia=\frac{1}{2}\frac{γ_w R_H^2}{η}inA\)
Since n=e/(1+e),
∴ \(q=C_S \frac{γ_w R_H^2}{η}\frac{e}{1+e}iA.\)
Sanfoundry Global Education & Learning Series – Soil Mechanics.
To practice all areas of Soil Mechanics, here is complete set of 1000+ Multiple Choice Questions and Answers.
