This set of Aptitude Questions and Answers (MCQs) focuses on “Cube Root”.
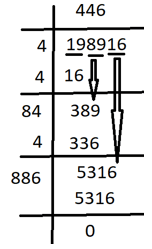
1. Find the digit in the unit’s place in the square root of 198916.
a) 6
b) 2
c) 4
d) 8
View Answer
Explanation: The digit in the unit’s place in the square root of 198916 is 6.
2. How many perfect squares lie between 300 and 1000?
a) 15
b) 14
c) 12
d) 13
View Answer
Explanation: Perfect squares between 300 and 1000 are 324, 361, 400, 441, 484, 529, 576, 625, 676, 729, 784, 841, 900 and 961.
Hence, there are 14 perfect squares that lie between 300 and 1000.
3. A woman was born in the first half of the eighteenth century and was p years old in the year p2. In which year she was born?
a) 1716
b) 1736
c) 1722
d) 1708
View Answer
Explanation: Clearly 422 = 1764.
So, the woman is 42 years old in the year 1764.
Therefore, she was born in (1764-42) = 1722, which lies in the first half of eighteenth century.
4. Find the value of n if \(\sqrt{5^n}\)=625.
a) 7
b) 6
c) 3
d) 8
View Answer
Explanation: \(\sqrt{5^n}\)=625=54.
5n=58.
Hence, n = 8.
5. What percentage of numbers from 51 to 100 have squares that end in the digit 1?
a) 20%
b) 10%
c) 1%
d) 25%
View Answer
Explanation: The numbers from 51 to 100 which has 1 in the unit digit in its square are, 51, 59, 61, 69, ……, 91, 99. There are 10 numbers out of 50.
Therefore, required percentage = \(\frac{10}{50}\)*100=20%.
6. How many 3-digit numbers satisfy the condition that the last digit of the square of 3-digit number is 3?
a) 10
b) 0
c) 20
d) 9
View Answer
Explanation: Square numbers either end with 1, 4, 5, 6, 9 or 0. No square numbers end with 3.
Therefore, 3-digit numbers satisfy the condition that the last digit of the square of 3-digit number is 3 is zero.
7. If \(\sqrt{(a-3)(b+2)}\)=11, a and b being positive integers less than 20, find the value of a and b.
a) 13, 8
b) 15, 10
c) 14, 9
d) 7, 19
View Answer
Explanation: 11 is a prime number and its square 121 is divisible by 11 or 1.
Since, a and b being positive integers less than 20, (a-3)=11 🡪 a = 14 and (b+2)=11 🡪 b = 9.
8. Which one of the following numbers has rational square root?
a) 0.009
b) 0.016
c) 2.5
d) 0.04
View Answer
Explanation: \(\sqrt{0.009}\)=0.0948…,\(\sqrt{0.016}\)=0.1234…,\(\sqrt{2.5}\)=1.5811…and \(\sqrt{0.04}\)=0.2.
Therefore, 0.04 has rational square root.
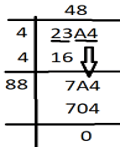
9. If 23A4 is perfect square, then find the value of A.
a) 0
b) 2
c) 4
d) 6
View Answer
Explanation: 482 = 2304. Therefore, A = 0
10. Find the smallest perfect square that is divisible by 5!.
a) 1600
b) 3600
c) 900
d) 2500
View Answer
Explanation: 5! = 120 = 5*4*3*2*1 = 22*2*3*5. To make it a perfect square, it should be multiplied by 2*3*5 i.e., 30. Hence, the smallest perfect square that is divisible by 5! is 120*30 = 3600.
To practice all aptitude questions, please visit “1000+ Quantitative Aptitude Questions”, “1000+ Logical Reasoning Questions”, and “Data Interpretation Questions”.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
