This set of Aptitude Questions and Answers (MCQs) focuses on “Division Algorithm – Set 2”.
1. A number being successively divided by 5, 7 and 9 leaves remainder 2, 4 and 6 respectively. Find the respective remainders if the order of the divisors is reversed.
a) 7, 4, 3
b) 5, 4, 3
c) 5, 2, 1
d) 7, 2, 1
View Answer
Explanation: Let the number be x and corresponding quotients when divided by 5, 7 and 9 be y, z and 1 respectively.
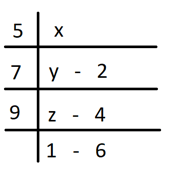
z = 9*1 + 6 = 15
y = 7z + 4 = 7*15 + 4 = 109
x = 5y + 2 = 5*109 +2 = 547
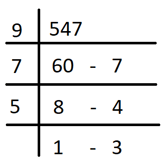
Respective remainders when the order of the divisors is reversed are 7, 4 and 3 respectively.
2. If seven times the smaller number is divided by the larger one, we get 5 as quotient and 1 as remainder. Also, if three times the larger number is divided by the smaller one, we get 4 as quotient and 3 as remainder. Find the numbers.
a) 12 and 18
b) 25 and 18
c) 24 and 18
d) 18 and 36
View Answer
Explanation: Let the larger number be x and the smaller number be y.
Then, 7y = 5x +1 …… (i)
And 3x = 4y + 3 …… (ii)
Solving (i) and (ii), we get,
x = 25 and y = 18
Hence, the numbers are 25 and 18.
3. Three girls X, Y and Z were asked to divide a certain number by 1547 by the method of factors. They took the factors in the order (7,13,17), (13,17,7) and (17,7,13) respectively. If the first girl X obtained (2,3,5) as successive remainder, then find the successive remainders obtained by the other two girls Y and Z.
a) (2,1,2) and (5,5,3)
b) (2,1,2) and (15,15,3)
c) (2,1,2) and (15,5,3)
d) (2,2,2) and (15,5,3)
View Answer
Explanation: Let the number be x and corresponding quotients when divided by 1, 13 and 17 be y, z and 1 respectively.
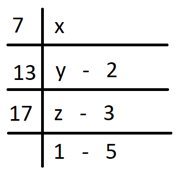
z = 17*1 + 5 = 22
y = 13*22 + 3 = 289
x = 289*7 + 2 = 2004
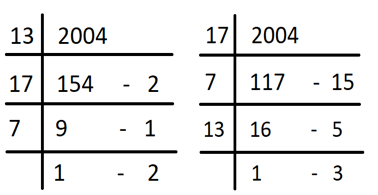
The successive remainders obtained by the other two girls Y and Z are (2,1,2) and (15,5,3) respectively.
4. 11 is added to a certain number, the sum is multiplied by 7, the product is divided by 6 and finally 2 is subtracted from the quotient. Thus, if the remainder left is 12, what was the original number?
a) 15
b) 22
c) 37
d) 1
View Answer
Explanation: \(\frac{(x+11)*7}{6}\)-2=12
(x + 11)*7 = 84
x = 1.
5. Find the remainder when (103 + 93)652 is divided by 123.
a) 1
b) 1000
c) 752
d) 754
View Answer
Explanation: \(\frac{1729^{652}}{1728}=\frac{(1729^{652}-1)+1}{1728} \)
1729652 – 1 is divisible by 1728. Hence, the remainder is 1.
6. Find the 2-digit number, the quotient of whose division by the product of its digit is equal to 9/2, and the difference between the required number and the number consisting of the same digits written in reverse order is 63.
a) 81
b) 92
c) 61
d) 72
View Answer
Explanation: Let the required 2-digit number be (10x+y) and reverse of the number be (10y+x).
From data, \(\frac{10x+y}{xy}=\frac{9}{2} \)
i.e., 20x + 2y = 9xy …… (i)
Also, (10x+y) – (10y+x) = 63
i.e., x – y = 7 …… (ii)
Solving (i) and (ii), we get
x = 8 and y = 1
Hence, the required number is 81.
7. Find the 2-digit number if it is known that the ratio of the required number and the sum of its digit is 7 and also the quotient of the product of its digit and that of the sum is 8/3.
a) 48
b) 84
c) 72
d) 94
View Answer
Explanation: Let the required number be (10x+y). The sum and product of the number is x+y and xy respectively.
By data, \(\frac{10x+y}{x+y}\)=7
i.e., x = 2y …… (i)
Also, \(\frac{xy}{x+y}=\frac{8}{3} \)
i.e., 8x + 8y = 3xy …… (ii)
Solving (i) and (ii), we get,
x = 8 and y = 4.
Hence, the required number is 84.
8. 912 – 512 is divisible by which of the following number?
a) 56
b) 106
c) 106 or 56
d) 106 or 56 or 14
View Answer
Explanation: We know that a3 – b3 = (a-b)(a2+b2+ab) and a2 – b2 = (a+b)(a-b).
912 – 512 = (94)3 – (54)3 = (94-54)(98+58+98*58) = (92-52)(92+52) (98+58+98*58)
= (9+5)(9-5)(92+52)(98+58+98*58)
92-52=56, 9+5=14, 92+52=106.
Hence, 912 – 512 is divisible by 106 or 56 or 14.
9. If we divide the unknown 2-digit number by the number consisting of the same numbers in reverse order, we get 2 as quotient and 10 as a remainder. If we divide the required number by the sum of its digits, we get 7 as quotient and 6 as a remainder. Find the number.
a) 62
b) 26
c) 84
d) 95
View Answer
Explanation: Let the required 2-digit number be (10x+y), sum of its digits be (x+y) and reverse of the number be (10y+x).
By data, (10x + y) = 2(10y + x) + 10
i.e., 8x – 19y = 10 …… (i)
Also, (10x + y) = 7(x + y) + 6
i.e., x – 2y = 2 …… (ii)
Solving (i) and (ii), we get,
x = 6 and y = 2
Hence, the required number is 62.
10. Find the greatest common divisor of 2200-1 and 2240-1.
a) 240-1
b) 220-1
c) 210-1
d) 260-1
View Answer
Explanation: The GCD of (Ax-1) and (Ay-1) is given by (AGCD of x and y-1).
Hence, the required answer is 240-1.
To practice all aptitude questions, please visit “1000+ Quantitative Aptitude Questions”, “1000+ Logical Reasoning Questions”, and “Data Interpretation Questions”.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
