This set of Aptitude Questions and Answers (MCQs) focuses on “Base System”.
1. What will be the number of y digit numbers in the nth base system?
a) ny
b) ny-1
c) ny-n
d) ny-ny-1
View Answer
Explanation: Given base n and digit y.
We know that for base n and digit y, the required number of numbers is ny-ny-1.
2. What is the number of 6-digit numbers in the binary system?
a) 16
b) 8
c) 32
d) 64
View Answer
Explanation: We know that for base n and digit y, the required number of numbers is ny-ny-1.
Here base is 2 and digit is 6. Hence, the number of 6-digit numbers in the binary system = 26-25 = 32.
3. What will be the number is decimal system if it is 203 in base 5?
a) 53
b) 65
c) 35
d) 47
View Answer
Explanation: (203)5 = (?)10
= 2*52 + 0*51 + 3*50.
= 50 + 0 + 3 = 53.
4. Find the value of x in the equation (53)7 + (25)8 = (x)10.
a) 39
b) 59
c) 47
d) 49
View Answer
Explanation: (53)7 = 5*71 + 3*70 = 35 + 3 = (38)10.
(25)8 = 2*81 + 5*80 = 16 + 5 = (21)10.
Therefore, (53)7 + (25)8 = (38)10 + (21)10 = (59)10.
5. What will be the number is binary system if it is 48 decimal system?
a) 110000
b) 111000
c) 101000
d) 101010
View Answer
Explanation: In order to convert decimal to binary system, we need to divide the number by 2 and write down the remainder from bottom to top, that will be the number in binary system.
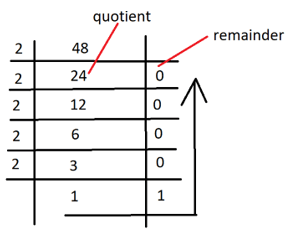
Therefore, (48)10 = (110000)2.
6. Find the value of x in the equation (111.01)2 = (x)10.
a) 5.5
b) 6.75
c) 7.25
d) 7.5
View Answer
Explanation: (111.01)2 = 1*22 + 1*21 + 1*20 + 0*2-1 + 1*2-2
= 4 + 2 + 1 + 0 + .25 = (7.25)10 = (x)10.
7. Find the value of x in the equation (1331)10 / (11)10 = (x)16.
a) 75
b) 79
c) 69
d) 65
View Answer
Explanation: \(\Big(\frac{1331}{11}\Big)\)=121, in decimal system.
(1331)10 / (11)10 = (121)10 = (x)16
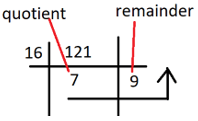
Therefore, (1331)10 / (11)10 = (121)10 = (79)16 = (x)16.
8. Find the value of x in the equation (1AB)16 * (11)4 = (x)5.
a) 45050
b) 33202
c) 23030
d) 32020
View Answer
Explanation: In base 16, we know that A=10 and B=11.
(1AB)16 = 1*162 + A*161 + B*160 = 256 + 10*16 + 11*1 = (427)10.
(11)4 = 1*41 + 1*40 = 4 + 1 = (5)10.
(1AB)16 * (11)4 = (427)10 * (5)10 = (2135)10.
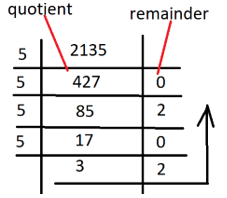
(1AB)16 * (11)4 = (2135)10 = (32020)5 = (x)5.
9. In base 7, find the square root of greatest 3-digit perfect square.
a) 31
b) 28
c) 25
d) 22
View Answer
Explanation: In decimal system 312 i.e., 961 is the greatest 3-digit perfect square.
In base system 9, 282 i.e., (784)10 = (961)9 is the greatest 3-digit perfect square.
In base system 8, 252 i.e., (625)10 = (961)8 is the greatest 3-digit perfect square.
In base system 7, 222 i.e., (484)10 = (961)7 is the greatest 3-digit perfect square.
10. In base 8, find the greatest 4-digit perfect square.
a) 9801
b) 8701
c) 7601
d) 7744
View Answer
Explanation: In base 10, the greatest 4-digit perfect square is 9801.
In base 9, the greatest 4-digit perfect square is 8701.
In base 8, the greatest 4-digit perfect square is 7601.
772 = (5929)10 = (7601)8.
To practice all aptitude questions, please visit “1000+ Quantitative Aptitude Questions”, “1000+ Logical Reasoning Questions”, and “Data Interpretation Questions”.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
