Here are 1000+ Quantitative Aptitude Questions and Answers (Topic wise).
1. Which of the following is a prime number?
a) 517
b) 559
c) 571
d) 533
View Answer
Explanation: We know that, (24)2 > 571,517,533,559
Prime numbers less than 24 are 2, 3, 5, 7, 11, 13, 17, 19, 23.
517 is divisible by 11.
533 and 559 are divisible by 13.
Clearly, none of them divides 571. Hence, it is a prime number.
2. Find the sum of first 90 even natural numbers.
a) 8180
b) 8190
c) 8100
d) 8110
View Answer
Explanation: We know that, sum of first n even natural number is given by n2+n.
Therefore, the sum of first 90 even natural numbers = 902+90 = 8190.
3. Find the sum two numbers, whose product is 200 and difference is minimum.
a) 30
b) 27
c) 35
d) 33
View Answer
Explanation: x & y be the two numbers.
Given that x*y = 200 and x-y = minimum.
The factor pairs are (1,200), (2,100), (4,50), (5,40), (8,25) and (10,20).
The only pair which satisfy both the condition is 10,20.
Hence, their sum is 30.
4. Find the ten’s digit in the expression 652 – 552?
a) 2
b) 6
c) 5
d) 0
View Answer
Explanation: 652 – 552 = (65+55) (65-55) = 120*10.
Therefore, ten’s digit of the expression is 0.
5. A number when divided by 91 leaves a remainder 65. If the same number is divided by 13, find the remainder.
a) 7
b) 0
c) 5
d) 12
View Answer
Explanation: On dividing the given number by 91, let k be the quotient and 65 the remainder.
Then, number = 91k + 65 = 13*7k + 13*5 = 13(7k + 5).
The number is completely divisible by 13. Hence the remainder is 0.
6. Find the highest power of a number 18 in 100!.
a) 24
b) 18
c) 28
d) 12
View Answer
Explanation: 18 on prime factorization yields 2*32.
In 100!, power of 32 is less than power of 2. So, we shall find power of 32 i.e., 9 in 100!.
Highest power of 9 i.e., 32 in 100! = \(\Big(\frac{100}{3}+\frac{100}{3^2}+\frac{100}{3^3}+\frac{100}{3^4}\Big)\)/2 = (33 + 11 + 3 + 1)/2 = 24.
Therefore, highest power of a number 18 in 100! Is 24.
7. When 8255 is divided by 511, what is the remainder?
a) 510
b) 10
c) 1
d) 500
View Answer
Explanation: \(\frac{8^{255}}{511}=\frac{8^{3*85}}{511}=\frac{512^{85}}{511}=\frac{(511+1)^{85}}{511} \)
Therefore, 1 is the remainder.
8. How many distinct prime factors are there in 9900?
a) 7
b) 4
c) 27
d) 54
View Answer
Explanation: The number 9900 can be factorized into, 9900 =22*32*52*11.
Hence, there are 4 distinct prime factors i.e., 2, 3, 5 and 11.
9. Find the value of 5358*54.
a) 283932
b) 298332
c) 289322
d) 289332
View Answer
Explanation: 5358*54 = 5358 * (50+4) = 267900 + 21432 = 289322.
10. Find the HCF of 405, 585, 765 and 900.
a) 35
b) 15
c) 45
d) 90
View Answer
Explanation: The difference between 405 and 585 is 180 = 45*4.
The difference between 585 and 765 is 180 = 45*4.
The difference between 765 and 900 is 135 = 45*3.
The difference between 405 and 900 is 495 = 45*11.
Therefore, the HCF of 405, 585, 765 and 900 is 45.
11. Two numbers are in the ratio 4:5. Their LCM is 240. Find the sum of numbers.
a) 108
b) 120
c) 132
d) 98
View Answer
Explanation: Let the two numbers be 4x and 5x, then their LCM is 20x.
LCM 20x = 240, hence x=12.
The numbers are 4*12=48 and 5*12=60.
Therefore, sum of the numbers is 48+60 = 108.
12. A man travelled 30% of his journey at a speed of 85 kmph and the rest of his journey at a speed of 33 kmph. Find his average speed throughout the journey.
a) 46.6 kmph
b) 48.6 kmph
c) 42.6 kmph
d) 44.6 kmph
View Answer
Explanation: The average speed of the man = [(30 * 85) + (70 * 33)] / 100 = (2550 + 2310) / 100 = 4860 / 100 = 48.6 kmph
13. Find the value of \(\frac{0.49-0.25}{0.2}\)?
a) 1.02
b) 1.04
c) 1.2
d) 1.4
View Answer
Explanation: \(\frac{0.49-0.25}{0.2}=\frac{0.7^2-0.5^2}{0.7-0.5}=\frac{(0.7+0.5)(0.7-0.5)}{0.7-0.5}\)=1.2 .
14. Which of the following fraction is greater than 1/2 and less than 5/9?
a) 2/3
b) 5/8
c) 4/7
d) 6/11
View Answer
Explanation: \(\frac{1}{2}\)=0.5 and \(\frac{5}{9}\)=0.5.
\(\frac{6}{11}\)=0.54,\(\frac{4}{7}\)=0.5714,\(\frac{2}{3}\)=0.6 and \(\frac{5}{8}\)=0.625.
Therefore, 6/11 is greater than 1/2 and less than 5/9.
15. If a-b=16 and a2-b2=544, find the value of 2ab.
a) 450
b) 500
c) 550
d) 350
View Answer
Explanation: a – b = 16 …… (i)
a2-b2 = (a+b) * (a-b) = 544.
a + b = 34 …… (ii)
On solving (i) and (ii), we get,
a = 25 and b = 9.
Therefore, 2ab = 2*25*9 = 450.
16. If R = xS – 4, when S = 5 and R = 16. Then find the value of R when S = 8.
a) 36
b) 28
c) 32
d) 34
View Answer
Explanation: R = xS – 4 🡪 16 = 5x – 4 🡪 x = 4.
R = 4*8 – 4 = 28.
17. Find the square-root of 44521.
a) 221
b) 219
c) 211
d) 229
View Answer
Explanation:
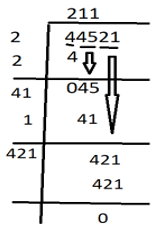
Therefore, square-root of 44521 = 211.
18. The speed of a boat upstream is 20 kmph find the speed of the boat downstream if the speed of the stream is 3 kmph.
a) 26 kmph
b) 25 kmph
c) 23 kmph
d) 22 kmph
View Answer
Explanation: The speed of the boat downstream = speed of the boat up stream + 2 * speed of the stream = 20 + 3 * 2 = 26 kmph.
19. Find the smallest number that should be added to 2190 to make it a perfect cube.
a) 21
b) 7
c) 29
d) 13
View Answer
Explanation: We know that, 123 = 1728 and 133 = 2197.
2197 – 2190 = 7.
Therefore, the smallest number to be added is 7.
20. The age of 5 people are in proportion 2:3:4:10:11. If their average age is 18, find the average age of the eldest of them.
a) 22
b) 11
c) 44
d) 33
View Answer
Explanation: The eldest person has a share of 11 from the proportion, so, let the age of the eldest from them be 11x.
The total of the proportion = (2 + 3 + 4 + 10 + 11) x = 30x
The average of the proportion = 30x / 5 = 6x
Average age as per proportion = 6x
Average age given = 18
On putting values, 6x = 18, x = 3
The age of the eldest person = 11x = 11 * 3 = 33.
21. The average age of 9 members of a family is 68. If a couple with average age 45 left the house and another couple is blessed with twins, what will be the average age of the family 5 years later?
a) 63
b) 60
c) 53
d) 57
View Answer
Explanation: The total age of the family now = 9 * 68 = 612
The age of the couple left = 45 * 2 = 90
The total age now = 612 – 90 = 522
The total age 5 years hence = 522 + (9 * 5) = 522 + 45 = 567 (the number of people in the family remains constant as two people left, and a pair of twins was born the same year).
The average age of the family = 567 / 9 = 63.
22. There are 40 animals in a zoo and per animal 20 packets of milk is required. One pack of milk contains 200 ml of milk, and milk costs 46 rupees per litre. If the employees of the zoo fulfil only 80% of the animal’s intake of milk what will be the expenditure of the zoo?
a) 546.9
b) 576.5
c) 579.6
d) 587.8
View Answer
Explanation: Total amount of milk required = 40 * 20 * 200 ml = 16000 ml = 16 litres of milk
Milk given = 80% of required = 16 * 80 / 100 = 12.6 L
Cost of the milk = 12.6 * 46 = 579.6
23. In a group of 10 girls 5 have an average height of 5.2 feet. Rest of the 5 girls have an average height of 1.7 metres. Find the average height of the group in feet. (1 m = 3.281 feet).
a) 5.3
b) 5.4
c) 5.1
d) 5.2
View Answer
Explanation: Total height of first 5 girls of the group = 5.2 * 5 = 26 feet
Total height of next 5 girls = 1.7 * 5 = 8.5 metres
8.5 metres to feet = 8.5 * 3.281 ≈ 27.89
Total height of the girls = 27.89 + 26 = 53.89 feet
Average height = 53.89 / 10 = 5.389 ≈ 5.4 feet
24. P is thrice as old as Q. The difference between the ages of P and Q is a multiple of 9. Find the minimum possible age of P, if it is known that Q’s age is an odd prime number.
a) 12 years
b) 11 years
c) 10 years
d) 9 years
View Answer
Explanation: Let the age of P and Q be x and y.
The minimum possible age of Q can be 3 as the age is a prime number and an odd number.
The minimum difference between their ages can be 9 as the number should be a multiple of 9.
P’s minimum possible age can be Q’s minimum possible age + minimum possible difference.
3 + 9 = 12 years
25. When my parents married their age was in a ratio 11 : 10 (father’s age : mother’s age). This year they celebrated 15th anniversary. If the total of their ages at their silver jubilee anniversary will be 113, find my father’s age now.
a) 40 years
b) 33 years
c) 48 years
d) 42 years
View Answer
Explanation: The total of my parent’s age at their silver jubilee = 113 years (given)
The total of my parent’s age when they got married = Total age after 25 years of marriage – 2 * 25
113 – 50 = 63
Total age 15 years before = 63 years
Individual age 15 years before:
Ratio of their ages then = 11 : 10
Let their ages then be in terms of x.
11x + 10x = 63
21x = 63
X = 63 / 21 = 3
Father’s age then = 11x = 11 * 3 = 33
Father’s age now = 33 + 15 = 48 years
26. The age of 5 people are in a ratio 2 : 3 : 4 : 5 : 6. If the age of the eldest of them is 42 years, find the average of their ages.
a) 27 years
b) 28 years
c) 25 years
d) 26 years
View Answer
Explanation: Let the ages of the following people be in terms of a constant x.
The age in terms of x will be 2x, 3x, 4x, 5x, and 6x.
The age of the eldest person = 6x = 42 years
6x = 42 years
X = 42 / 6 =7 years
2x = 2 * 7 = 14 years
3x = 3 * 7 = 21 years
4x = 4 * 7 = 28 years
5x = 5 * 7 = 35 years
The respective ages of these 5 people are 14, 21, 28, 35 and 42 years.
The sum of these ages = 14 + 21 + 28 + 35 + 42 = 140
Average age of the members = 140 / 5 = 28 years
27. What should be the value of log10 (0.0000001)?
a) -1/7
b) -1
c) -7
d) 7
View Answer
Explanation: log10 (0.0000001) = log10 (1/10000000)
= log10 (1/107)
= log10 (10-7)
= -7 log1010
= -7 * 1
= -7
28. Which set of values of z satisfy log (z2 – 6z + 6) = 0?
a) 3 and 2
b) 5 and 1
c) 4 and 6
d) 1 and 2
View Answer
Explanation: Given,
log (z2 – 6z + 6) = 0
➩ z2 – 6z + 6 = 100
➩ z2 – 6z + 6 = 1
➩ z2 – 6z + 5 = 0
➩ z2 – 5z – 1z + 5 = 0
➩ z(z – 5) + (- 1) (z – 5) = 0
➩ Thus, z = 1 and 5 satisfies the equation.
29. Find 112% of a number if 20% of the number is 120.
a) 692
b) 662
c) 652
d) 672
View Answer
Explanation: Let the number be x.
20% of a number = 120
20% of x = 120
20 * x / 100 = 120
x / 5 = 120
x = 120 * 5 = 600
112% of the number:
112 % of 600 =
112 * 600 / 100 = 112 * 6 = 672
30. What percent of 50 is 0.005% of 10000?
a) 10%
b) 1%
c) 100%
d) 0.1%
View Answer
Explanation: 0.005% of 10,000 = 0.005 * 10,000 / 100 = 0.5
Percentage of 50 equivalent to 0.5 = 0.5 / 50 * 100 = 1%
31. The purchase price of an article is 20% less than the profit made. Find the profit if the selling price is 360 rupees.
a) 180 rupees
b) 240 rupees
c) 200 rupees
d) 160 rupees
View Answer
Explanation: The purchase price is 20% less than the profit made.
Let the profit made be x.
The purchase price = x – 20% of x = 0.8x
X + 0.8x = 360
1.8x = 360
X = 200 rupees
32. The cost price of an article is 1.56 times the selling price. Find the loss percentage.
a) 37.8%
b) 35.9%
c) 39.5%
d) 34.5%
View Answer
Explanation: Let the selling price be x.
The cost price = 1.56 times the selling price = 1.56x
Loss = cost price – selling price = 1.56x – x = 0.56x
Loss percentage = 0.56 / 1.56 * 100 = 35.89% ≈ 35.9%
33. A shopkeeper purchased an article for 500 rupees. At what price should he mark the article to allow a discount of 35% and still earn 100% profit.
a) 1599 rupees
b) 1523 rupees
c) 1575 rupees
d) 1539 rupees
View Answer
Explanation: The cost price for the shopkeeper is 500 rupees.
The discount percentage is 35%.
The profit is 100%.
Profit = 100% of 500 = 500
The profit = 500, cost price = 500
Selling price = 500 + 500 = 1000
The selling price = 1000
Marked price = selling price + discount
Let the marked price be x.
X = 1000 + 35% of x
X = 1000 + 0.35x
0.65x = 1000
X = 1000 / 0.65 = 1538.46 rupees ≈ 1539 rupees
34. The product of two numbers is 10 more than 5 times the sum times the sum. Find the numbers if the numbers are in a ratio 5 : 6.
a) 15, 18
b) 20, 24
c) 10, 12
d) 5, 6
View Answer
Explanation: Let the ratios be in terms of x.
The numbers will be 5x and 6x.
The product of the numbers = 30x2
The sum of the numbers = 6x + 5x = 11x
Now it is giving that 30x2 = 5 * 11x + 10 = 55x + 10
30x2 = 55x + 10
On solving the quadratic equation, we get x = 2
The numbers are 10 and 12.
35. A mixture contains milk and water in a ratio 5 : 9. When 5 liters of water is added the ratio changes to 5 : 11. Find the quantity of milk in the initial mixture.
a) 15 liters
b) 12.5 liters
c) 17 liters
d) 10.5 liters
View Answer
Explanation: Let the quantities of milk and water be in terms of x.
The initial quantity of milk and water = 5 : 9 = 5x : 9x
The changed quantity of milk and water = 5 : 11 = 5x : 11x
On adding 5 liters of water the quantity of water changed from 9x to 11x
11x – 9x = 2x
2x = 5 liters of water
X = 2.5
The initial quantity of milk = 5x = 5 * 2.5 = 12.5 liters.
36. There are a total of 1236 students in a school. If the boy to girl ratio is 1 : 2, find the difference between number of girls and boys.
a) 412
b) 824
c) 241
d) 214
View Answer
Explanation: The number of girls = 1236 / 3 * 2 = 412 * 2 = 824
Number of boys = 1236 / 3 * 1 = 412
Difference = 824 – 412 = 412
37. 2 friends a and b started a company with 20000 and 30000, respectively. If there was a profit of 12995 rupees at the end of the year find their monthly profit of a.
a) 491.8 rupees
b) 431.16 rupees
c) 1082.91 rupees
d) 649.75 rupees
View Answer
Explanation: The profit after 12 months = 12995 rupees
Monthly profit = 12995 / 12 = 1082.91 rupees per month
The individual profit of a and b are in the ratio of their investment = 2 : 3
Their individual profit = 1082.91 / 5 * 2, 1082.92 / 5 * 3 = 431.16, 649.75 rupees
The monthly profit of a = 431.16 rupees.
38. A and b were partners in a firm. A invested 12000 on the first day of the business and b invested 30000 after 6 months of the commencement of the business. If a retired after 8 months of the commencement of the business, find the profit – sharing ratio of a to b after a year.
a) 8 : 15
b) 7 : 12
c) 3 : 14
d) 9 : 16
View Answer
Explanation: The profit – sharing ratio of a to b:
The profit – sharing ratio will be a’s investment * a’s time of investment : b’s investment * b’s time of investment = 12000 * 8 : 30000 * 6 = 96000 : 180000 = 8 : 15
39. 3 pipes A, B and C can fill a tank in 50 minutes, 120 minutes, and 60 minutes, respectively. If all the pipes are opened together, how much time is required to fill 27% of the tank?
a) 10 minutes
b) 2 minutes
c) 4 minutes
d) 6 minutes
View Answer
Explanation: Let the capacity of the tank be 600 litres.
The efficiencies of the pipes = 600 / 50, 600 / 120, 600 / 60 = 12, 5, 10 litres
The total efficiency of the pipes = 12 + 5 + 10 = 27 litres
To fill 27% of the tank that is 27 * 600 / 100 = 162 litres
162 / 27 = 6 minutes
40. 3 pipes can empty a semi filled tank in 4 minutes, 5 minutes and 6 minutes, respectively. If all the pipes are opened simultaneously, how long does it take to empty a filled tank?
a) 3.24 minutes
b) 2.34 minutes
c) 3.42 minutes
d) 2.43 minutes
View Answer
Explanation: The time taken by the 3 pipes to empty a fully filled tank = 8 minutes, 10 minutes and 12 minutes respectively.
Let the capacity of the tank be 120 liters.
The efficiency of the pipes = 120 / 8, 120 / 10 and 120 / 12 respectively = 15, 12, 10 respectively.
The relative efficiency = 15 + 12 + 10 = 37
The time required = 120 / 37 = 3.24 minutes
41. 64 men can do a piece of work in 90 days. Find the amount of work done by 95 men in 50 days.
a) 84%
b) 85%
c) 83%
d) 82%
View Answer
Explanation: The Total work to be done = 64 * 90 = 5760 units
The amount of work done = 95 * 50 = 4750 units
The percentage of work done = 4750 / 5760 * 100 = 82.46%
42. A group of 5 men or 12 women can do a task in 78 days. find the time taken by 5 men and 12 women to complete the task.
a) 39 days
b) 36 days
c) 29 days
d) 26 days
View Answer
Explanation: The time taken by 5 men = time taken by 12 women.
The efficiency of 5 men = efficiency of 12 women
Let the efficiency of a man be 12x.
The efficiency of a woman = 12x * 5 / 12 = 5x
The total efficiency of 5 men and 12 women = 12x * 5 + 5x * 12 = 120x
The total work = 78 * 60x
The time taken = 78x * 60 / 120x = 39 days
43. The speed of a train is 120 kmph and the length of the train is 240 m. find the time it will take to cross a pole.
a) 9.6 seconds
b) 7.2 seconds
c) 4.8 seconds
d) 2.4 seconds
View Answer
Explanation: The distance to be covered = 240 m
The speed = 120 kmph
The speed in meter per second = 120 * 5 / 18 = 100 / 3
The time taken = 240 / 100 * 3 = 7.2 seconds.
44. Two trains cross each other at a speed of 30kmph and 45 kmph, respectively. If they are moving in the opposite direction, find the length of both the trains combined. The time taken = 12 seconds.
a) 0.30 km
b) 0.32 km
c) 0.25 km
d) 0.33 km
View Answer
Explanation: The relative speed = 30 + 45 = 75 kmph = 20.83 m / s
The distance covered = 12 * 20.83 = 249.96 m = 0.25 km.
45. A mixture containing 50% of water is mixed with another mixture x% of water in the ratio 4 : 5. If the percentage of water in the new mixture is 40%, find the value of x.
a) 34
b) 40
c) 30
d) 32
View Answer
Explanation: The mixtures are mixed in a ratio 4 : 5.
Let the quantities of the mixture mixed be 400 liters and 500 liters, respectively.
The percentage of water in first mixture = 50% = 50% of 400 = 200 liters
The quantity of water in the second mixture = x% of 500 = 5x
The quantity of water in the final mixture = 40% of 900 = 360 liters
5x + 200 liters = 360 liters
5x = 360 – 200 = 160 liters
X = 160 / 5 = 32
X = 32
46. A man invested x rupees for 7.7 years at a rate of 13.3% simple interest. If the amount he received after 7.7 years was 23,68,197 rupees, find the amount he invested.
a) 11,70,000 rupees
b) 11,45,000 rupees
c) 12,70,000 rupees
d) 12,45,000 rupees
View Answer
Explanation: The amount he received = The amount he invested + the interest he received on the amount = x + x * 7.7 * 13.3 / 100 = x + 1.0241x = 2.0241x = 23,68,197 rupees.
2.0241x = 23,68,197 rupees, x = 23,68,197 / 2.0241 = 11,70,000 rupees.
47. What will be the area of a sector (in sq. cm.) of a circle with radius 42 cm and sector angle 240 degrees?
a) 5128
b) 3696
c) 4623
d) 3350
View Answer
Explanation: Area of sector = (angle in degree / 360) * πr2
➩ Area of sector = (240 / 360) * (22 / 7) * 42 * 42
➩ Area of sector = 3696 cm2
48. A triangle and a parallelogram are constructed on the same base such that their areas are equal. If the altitude of the parallelogram is 50 m, then what will be the altitude of the triangle?
a) 110 m
b) 50 m
c) 125 m
d) 100 m
View Answer
Explanation: Let the altitude of the triangle = H
Area of triangle = (1 / 2) * b * H
Area of rectangle = b * h
= b * 50
According to the question
➩ (1 / 2) * b * H = b * 50
➩ H = 2 * 50 m
➩ H = 100 m
49. What is the total surface area (in sq. m) of a covered rectangular tank having dimensions as 4m * 5m * 6m?
a) 98
b) 148
c) 74
d) 124
View Answer
Explanation: Given,
l = 4m, b = 5m, h = 6m
Total surface area = 2(lb + bh + hl)
= 2 (4 * 5 + 5 * 6 + 6 * 4)
= 2 (20 + 30 + 24)
= 2 (74)
= 148 m2
50. Today is Wednesday. After 81 days, what will be the day?
a) Thursday
b) Tuesday
c) Sunday
d) Saturday
View Answer
Explanation: Given, the day as Wednesday we have to find the day after 81 days.
As today is Wednesday, after 7 days it will be Wednesday and after 77 days also it will be Wednesday.
As 77th day is Wednesday, then after 81 days the day will be Sunday.
51. The selling price of 5 shares is equal to the face value of 3 shares. Find the profit or loss percentage.
a) 40% loss
b) 40% profit
c) 20% loss
d) 20% profit
View Answer
Explanation: Let the selling price of 1 share be 3 rupees.
The selling price of 5 shares = 15 rupees
The face value of 3 shares = 15 / 3 = 5 rupees
The face value is more than the selling price.
The loss = 5 – 3 = 2
The loss percentage = 2 / 5 * 100 = 40%
52. In how many ways we can select 5 members from a group of 9 people?
a) 120
b) 360
c) 720
d) 126
View Answer
Explanation: Given that, we have to select 5 members among 9 people.
So, nCr = n! / r!(n – r)!.
9C5 = 9! / 5!(9 – 5)! = 9 * 8 * 7 * 6 * 5! / (5! * 4!) = 126.
53. A bag contains 10 red cards and some yellow cards. If the probability of getting yellow cards is thrice the probability of getting a red card, then what is the number of yellow cards?
a) 15
b) 30
c) 20
d) 25
View Answer
Explanation: Given,
Red cards = 10
Let the yellow cards be x. Then total number of cards = 10 + x.
According to the question
x / (10 + x) = 3 * 10 / (10 + x)
➩ x = 30
54. An unbiased dice is thrown. What is the probability of getting 5 or a greater number?
a) 2 / 3
b) 5 / 6
c) 1 / 3
d) 1 / 3
View Answer
Explanation:
Possible outcomes = 1, 2, 3, 4, 5, 6
Favorable outcome = 5, 6
Probability = 2 / 6 = 1 / 3
55. If sin (20 + X) = cos 30, then what will be the value of X?
a) 70
b) 50
c) 40
d) 20
View Answer
Explanation: As we know,
Sin 60 = cos 30
➩ Sin (20 + X) = cos 30
Thus, X = 40.
Topic Wise Questions and Answers on Quantitative Aptitude

Data Interpretation:
Logical Reasoning:
1. Aptitude Questions on Number System
The section includes aptitude questions and answers on the number system, prime and co-prime numbers, real numbers, BODMAS simplification, progressions, multiplication shortcut methods, division algorithms, remainder theorem, factorials, divisibility rules for prime numbers and composite numbers, factors, and the sum of factors.
2. Quantitative Aptitude Questions on HCF and LCM
The section contains aptitude questions on hcf, lcm, hcf and lcm of algebraic variables, fractions and decimal numbers.
3. Aptitude Questions on Decimal Fractions
The section contains quantitative aptitude questions on decimal fractions, operations, and arithmetic operations.
|
|
|
4. Quantitative Aptitude Questions and Answers on Simplification
The section contains aptitude practice questions on simplification and simplification word problems.
5. Aptitude Questions on Square Roots and Cube Roots
The section contains aptitude questions with answers on square roots and cube roots.
|
|
|
6. Quantitative Aptitude Questions on Average
The section contains quantitative aptitude questions on average.
|
|
|
7. Problems on Ages
The section contains questions and answers on problems related to ages, involving two, three, and multiple individuals.
|
|
|
8. Questions and Answers on Logarithms
The section contains aptitude test questions on logarithms, functions and properties of logarithms, change of base, expanding and condensing logarithms.
9. Arithmetic Ability Questions on Percentage
The section contains aptitude questions for placement on percentage.
|
|
|
10. Questions on Profit and Loss
The section contains bank aptitude questions and answers on profit and loss, including problems related to cost price, selling price, discounts, and marked prices.
11. Arithmetic Ability Questions on Ratio and Proportion
The section contains questions and answers on ratio and proportion, word problems and series.
|
|
|
12. Bank Aptitude Questions on Partnership
The section contains quantitative aptitude questions and answers on partnership and partner retirement.
|
|
|
13. Pipes and Cisterns
The section contains arithmetic ability questions and answers on pipes and cistern, including problems involving two pipes and three pipes.
|
|
|
14. Time and Work Questions
The section contains questions and answers on time and work.
|
|
|
15. Time and Distance Questions
The section contains aptitude questions on time and distance.
|
|
|
16. Quantitative Questions on Boats and Streams
The section contains aptitude multiple choice questions and answers on boats and streams.
|
|
|
17. Problems on Trains
The section contains arithmetic questions and answers on problems involving trains, including problems related to trains and stations, two trains passing each other, and trains crossing poles.
|
|
|
18. Alligation or Mixture
The section contains arithmetic ability questions and answers on alligation or mixture.
|
|
|
19. Simple Interest Questions
The section contains quantitative aptitude questions and answers on simple interest, including problems focused on time, rate, and principal.
|
|
|
20. Aptitude Questions on Area
The section includes quantitative aptitude questions on the area of rectangles, squares, triangles, quadrilaterals, polygons, and circles.
|
|
|
21. Volume and Surface Area
The section contains aptitude questions on volume and surface area calculations for spheres, hemispheres, cylinders, cones, cubes, and cuboids.
22. Calendar
The section contains questions and answers on calendar concepts, including odd days, dates, years, and days of the week.
|
|
|
23. Stocks and Shares
The section contains aptitude questions with answers on stocks and shares, profit or loss on sales, revaluation, and the relationship between these financial values.
|
|
|
24. Permutations and Combinations
The section contains quantitative aptitude questions and answers on permutations and combinations.
|
|
|
25. Probability
The section contains objective questions and answers on probability.
|
|
|
26. Heights and Distances
The section contains questions and answers on applications of right triangles in geometry, including problems involving height and distance, angle of elevation, angle of depression, and multiple observers.
27. Data Interpretation
The section contains questions and answers on data interpretation.
|
|
|
28. Logical Reasoning
The section contains questions and answers on logical reasoning.
|
|
Wish you the best in your endeavor to learn and master Aptitude!
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
