This set of Thermodynamics Multiple Choice Questions & Answers (MCQs) focuses on “Boundary Work in a Multistep Process”.
1. A cylinder contains 1kg of ammonia. Initially the ammonia is at 180°C, 2 MPa and is now cooled to saturated vapour at 40°C, and then further cooled to 20°C, at which point the quality is 50%. Find the total work for the process, assuming a linear variation of P versus V.
a) -19.4 kJ
b) -29.4 kJ
c) -39.4 kJ
d) -49.4 kJ
View Answer
Explanation: State 1: (T, P) v1 = 0.10571 m3/kg; State 2: (T, x) sat. vap. P2 = 1555 kPa, v2 = 0.08313 m3/kg
State 3: (T, x) P3 = 857 kPa, v3 = (0.001638 + 0.14922)/2 = 0.07543 m3/kg
Work = ⌠PdV = (P1 + P2)m(v2 – v1)/2 + (P2 + P3)m(v3 – v2)/2
= (2000 + 1555)1(0.08313 – 0.10571)/2 + (1555 + 857)1(0.07543 – 0.08313)/2
= -49.4 kJ.
2. A piston cylinder has 1.5 kg of air at 300 K, 150 kPa. It is now heated up in a two step process. First constant volume to 1000 K (state 2) then followed by a constant pressure process to 1500 K, state 3. Find the work in the process.
a) 205.3 kJ
b) 215.3 kJ
c) 225.3 kJ
d) 235.3 kJ
View Answer
Explanation: 1 -> 2: Constant volume V2 = V1 and 2 -> 3: Constant pressure P3 = P2
State 1: T, P => V1 = mRT1/P1 = 1.5×0.287×300/150 = 0.861 m3
State 2: V2 = V1 => P2 = P1 (T2/T1) = 150×1000/300 = 500 kPa
State 3: P3 = P2 => V3 = V2 (T3/T2) = 0.861×1500/1000 = 1.2915 m3
Total work = P3(V3 – V2) = 500(1.2915 – 0.861) = 215.3 kJ.
3. A piston-cylinder assembly has 1kg of R-134a at state 1 with 600 kPa, 110°C, and is then brought to saturated vapour, state 2, by cooling. The cooling continues to state 3 where the R-134a is saturated liquid. Find the work in each of the two steps, 1 to 2 and 2 to 3.
a) 0, -20.22 kJ
b) -20.22 kJ,0
c) 0, 0
d) -20.22 kJ, -20.22 kJ
View Answer
Explanation: State 1: (T,P) => v = 0.04943 m3/kg; State 2: v2 = v1 and x2 = 1.0
v2 = v1 = vg = 0.04943 m3/kg => T = 10°C
State 3 reached at constant P (F = constant) v3 = vf = 0.000794 m3/kg
Since no volume change from 1 to 2 => 1W2 = 0
From 2 to 3: ∫P dV = P(V3 – V2) = mP(v3 – v2) = 415.8 (0.000794 – 0.04943)(1)
= -20.22 kJ.
4. R-22 is contained in a piston-cylinder, where the volume is 11 L when the piston hits the stops. The initial state is 150 kPa, −30°C with V=10 L. This system warms up to 15°C. Find the work done by R-22 during this process.
a) 0.35 kJ
b) 0.25 kJ
c) 0.15 kJ
d) 0.05 kJ
View Answer
Explanation: Initially piston floats, V < V(stop) so piston moves at constant P(ext) = P1 until it reaches the stops or 15°C, whichever is first. v1 = 0.1487 m3/kg; m = V/v = 0.010/0.1487 = 0.06725 kg
now, P1a = 150 kPa, v = V(stop)/m and v1a = V/m = 0.011/0.06725 = 0.16357 m3/kg
=> T1a = -9°C & T2 = 15°C
Since T2 > T1a then it follows that P2 > P1 and the piston is against stop.
Work = ∫ P(ext) dV = P9ext)(V2 – V1) = 150(0.011 – 0.010) = 0.15 kJ.
5. A piston-cylinder contains 50 kg of water at 200 kPa with V=0.1 m3. Stops in the cylinder restricts the enclosed volume to 0.5 m3. The water is now heated to 200°C. Find the work done by the water.
a) 50 kJ
b) 60 kJ
c) 70 kJ
d) 80 kJ
View Answer
Explanation: Initially the piston floats so the equilibrium lift pressure is 200 kPa
1: 200 kPa, v1= 0.1/50 = 0.002 m3/kg, and 2: 200°C
v(stop) = 0.5/50 = 0.01 m3/kg;
State 2 two phase => P2 = Psat(T2) = 1.554 MPa, V2 = V(stop) = 0.5 m3
1W2 = 1W(stop) = 200 (0.5 – 0.1) = 80 kJ.
6. Ammonia in a piston/cylinder arrangement is at 80°C, 700 kPa. It is now cooled at constant pressure to saturated vapour (state 2) at which point the piston is locked with a pin. The cooling continues to −10°C (state 3). Find the work.
a) -28.64 kJ/kg
b) -38.64 kJ/kg
c) -48.64 kJ/kg
d) -58.64 kJ/kg
View Answer
Explanation: 1W3 = 1W2 + 2W3 = ⌠PdV = P1(V2 – V1) = mP1(v2 – v1)
Since constant volume from 2 to 3; v1 = 0.2367 m3/kg, P1 = 700 kPa,
v2 = vg = 0.1815 m3/kg, 1w3 = P1(v2- v1) = 700 × (0.1815 – 0.2367)
= -38.64 kJ/kg.
7. A piston-cylinder contains 1 kg of liquid water at 300 kPa, 20°C. Initially the piston floats, with a maximum enclosed volume of 0.002 m3 if the piston touches the stops. Now heat is added so that the final pressure is 600 kPa. Find the work in the process.
a) 0.30 kJ
b) 0.40 kJ
c) 0.50 kJ
d) 0.60 kJ
View Answer
Explanation: State 1: Compressed liquid v = vf(20) = 0.001002 m3/kg
v(stop) = 0.002 m3/kg , 300 kPa
v2 = v(stop) = 0.002 m3/kg and V = 0.002 m3
Work is done while piston moves at P(lift) = constant = 300 kPa
1W2 = ∫ P dV = m*P(lift)*(v2 -v1) = 1 × 300(0.002 − 0.001002) = 0.30 kJ.
8. 10 kg of water in a piston-cylinder exists as saturated liquid/vapour at 100 kPa, with a quality of 50%. It is now heated till the volume triples. The mass of the piston is such that a cylinder pressure of 200kPa will float it. Find the work given out by the water.
a) 3090 kJ
b) 3190 kJ
c) 3290 kJ
d) 3390 kJ
View Answer
Explanation: Process: v = constant until P = P(lift) then P is constant.
State 1: v1 = vf + x vfg = 0.001043 + 0.5 × 1.69296 = 0.8475 m3/kg
State 2: v2, P2 ≤ P(lift) => v2 = 3 × 0.8475 = 2.5425 m3/kg;
T2 = 829°C ; V2 = m*v2 = 25.425 m3
Work = ∫ P dV = P(lift)×(V2 – V1) = 200 kPa × 10 kg × (2.5425 – 0.8475) m3/kg
= 3390 kJ.
9. Ammonia at 10°C with a mass of 10 kg is in a piston-cylinder arrangement with an initial volume of 1 m3. The piston initially resting on the stops has a mass such that a pressure of 900 kPa will float it. The ammonia is now slowly heated to 50°C. Find the work in the process.
a) 483.2 kJ
b) 583.2 kJ
c) 683.2 kJ
d) 783.2 kJ
View Answer
Explanation: Process: V = constant unless P = P(float)
State 1: T = 10°C, v1 = V/m = 1/10 = 0.1 m3/kg;
also v(f) < v < v(g) hence x1 = [v - v(f)]/v(fg) = (0.1-0.0016)/0.20381 = 0.4828 State 1a: P = 900 kPa, v = v1 = 0.1 < vg at 900 kPa; two-phase T1a = 21.52°C Since T2 > T1a then v2 > v1a
State 2: 50°C => 900 kPa which is superheated vapor hence
v2 = 0.1648 m3/kg, V2 = mv2 = 1.648 m3
Work = ∫ P dV = P(float) (V2 – V1) = 900 (1.648 – 1.0) = 583.2 kJ.
10. A piston-cylinder contains 0.1 kg saturated liquid and vapour water at 100 kPa with quality 25%. The mass of the piston is such that a pressure of 500 kPa will float it. The water is heated to 300°C. Find the work.
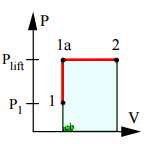
a) 2.91 kJ
b) 3.91 kJ
c) 4.91 kJ
d) 5.91 kJ
View Answer
Explanation: Process: v = constant until P = P(lift)
To locate state 1: v1 = 0.001043 + 0.25×1.69296 = 0.42428 m3/kg
1a: v1a = v1 = 0.42428 m3/kg > vg at 500 kPa, so state 1a is Sup.Vapor T1a = 200°C
State 2 is 300°C so heating continues after state 1a to 2 at constant P
=> 2: T2, P2 = P(lift) => v2 =0.52256 m3/kg ; V2 = mv2 = 0.05226 m3
1W2 = P(lift)*(V2 – V1) = 500(0.05226 – 0.04243) = 4.91 kJ.
11. A constant pressure piston cylinder contains 0.2 kg water in the form of saturated vapour at 400 kPa. It is now cooled to occupy half the original volume. Find the work in the process.
a) -12.5 kJ
b) -24.5 kJ
c) -8.5 kJ
d) -18.5 kJ
View Answer
Explanation: v1= 0.4625 m3/kg, V1 = mv1 = 0.0925 m3
v2 = v1/ 2 = 0.23125 m3/kg, V2 = V1 / 2 = 0.04625 m3
Process: P = C
W = ∫ PdV = P(V2-V1) = 400 kPa × (0.04625 – 0.0925) m3 = -18.5 kJ.
12. A piston cylinder contains air at 600 kPa, 290 K and volume of 0.01 m3. A constant pressure process gives out 54 kJ of work. Find the final temperature of the air.
a) 2700 K
b) 2800 K
c) 2900 K
d) 3000 K
View Answer
Explanation: W = ∫ P dV = P∆V hence ∆V = W/P = 54/600 = 0.09m3
V2 = V1 + ∆V = 0.01 + 0.09 = 0.1 m3
Assuming ideal gas, PV = mRT,
T2 = P2*V2/(m*R) = [(P2*V2)/(P1*V1)]*T1 = T1*(V2/V1) = (0.1*290)/0.01
= 2900 K.
13. A piston/cylinder has 5m of liquid 20°C water on top of piston with cross-sectional area of 0.1 m2. Air is let in under the piston that rises and pushes the water out. Find the necessary work to push all the water out.
a) 62.88 kJ
b) 52.88 kJ
c) 92.88 kJ
d) 42.88 kJ
View Answer
Explanation: P1 = Po + ρgH = 101.32 + 997 × 9.807 × 5 / 1000 = 150.2 kPa
∆V = H × A = 5 × 0.1 = 0.5 m3
Work = Area = ∫ P dV = ½ (P1 + Po )(Vmax -V1)
= ½ (150.2 + 101.32) kPa × 0.5 m3
= 62.88 kJ.
14. A piston/cylinder contains 1 kg water at 20°C with volume 0.1 m3. While the water is heated to saturated vapour, the piston is not allowed to move. Find the final temperature.
a) 201.7°C
b) 211.7°C
c) 215.7°C
d) 221.7°C
View Answer
Explanation: V2 = V1 = 0.1 m3
T2 = Tsat = 210 + 5[(0.1 – 0.10324)/(0.09361 – 0.10324)] = 211.7°C.
15. A piston cylinder contains 3 kg of air at 20°C and 300 kPa. It is now heated at a constant pressure to 600 K. Find the work in the process.
a) 244.2 kJ
b) 254.2 kJ
c) 264.2 kJ
d) 274.2 kJ
View Answer
Explanation: V1 = mR T1 / P1 = 3 × 0.287 × 293.15/300 = 0.8413 m3
V2 = mR T2 / P2 = 3 × 0.287 × 600/300 = 1.722 m3
work = ⌠ PdV = P (V2 – V1) = 300 (1.722 – 0.8413) = 264.2 kJ.
Sanfoundry Global Education & Learning Series – Thermodynamics.
To practice all areas of Thermodynamics, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
- Check Chemical Engineering Books
- Practice Chemical Engineering MCQs
- Check Thermodynamics Books
- Apply for Mechanical Engineering Internship
- Practice Mechanical Engineering MCQs
