Area of Quadrilaterals - Class 8 Maths MCQ

This set of Class 8 Maths Chapter 11 Multiple Choice Questions & Answers (MCQs) focuses on “Mensuration – Area of General Quadrilaterals”.

1. Find the area of the given quadrilateral.

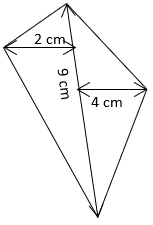
a) 26cm²
b) 27cm²
c) 29cm²
d) 25cm²
View Answer

Answer: b
Explanation: Area of general quadrilateral = \(\frac{1}{2}\) × (h₁ + h₂) × d [d – diagonal of quadrilateral]
= \(\frac{1}{2}\) × (4 + 2) × 9
= 27cm².

2. Find the height of the quadrilateral if the area is 144cm².

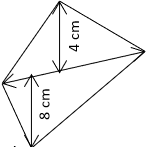
a) 24 cm
b) 12 cm
c) 22 cm
d) 11 cm
View Answer

Answer: a
Explanation: Area of general quadrilateral = \(\frac{1}{2}\) × (h₁ + h₂) × d (d – diagonal of quadrilateral)
⇒ 144 = \(\frac{1}{2}\) × (8 + 4) × d
⇒ d = 24 cm.

3. The area of quadrilateral PQRS is 228cm². Find length of QA.

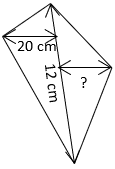
a) 16 cm
b) 9 cm
c) 8 cm
d) 18 cm
View Answer

Answer: d
Explanation: Area of general quadrilateral = \(\frac{1}{2}\) × (h₁ + h₂) × d (d – diagonal of quadrilateral)
⇒ 228 = \(\frac{1}{2}\) × (h₁ + 20) × 12
⇒ l(QA) = 18 cm.

4. Find the area of the shaded region. The length of the diagonal DB is 8 cm. The perpendicular distances from the vertices to the diagonal DB are 4 cm and 3 cm. The length of segment BC is 6 cm. (π = 3.14)

a) 21.87cm²
b) 9.87cm²
c) 13.87cm²
d) 17.87cm²
View Answer

Answer: c
Explanation: Area of shaded region = Area of general quadrilateral – Area of semicircle
= \(\frac{1}{2}\) × (h₁ + h₂) × d – \(\frac{\pi}{2}\) × (r)² = \(\frac{1}{2}\) × (4 + 3) × 8 – \(\frac{\pi}{2}\) × (3)² = 13.87cm².

5. Find the area of pentagon PQRSA. The perpendicular distances from the vertices to the diagonal PR are 5 cm and 2 cm.
Given: l(PR) = 10 cm, l(PA) = 8 cm, l(SA) = 7cm.

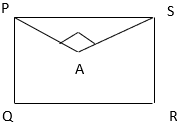
a) 7cm²
b) 6cm²
c) 8cm²
d) 5cm²
View Answer

Answer: a
Explanation: Area of pentagon PQRSA = Area of Quadrilateral PQRS – Area of Triangle PAS
= \(\frac{1}{2}\) × (h₁ + h₂) × d – \(\frac{1}{2}\) × b × h = \(\frac{1}{2}\) × (5 + 2) × 10 – \(\frac{1}{2}\) × 8 × 7 = 7cm².

Note: Join free Sanfoundry classes at Telegram or Youtube

Sanfoundry Global Education & Learning Series – Mathematics – Class 8.

To practice all chapters and topics of class 8 Mathematics, here is complete set of 1000+ Multiple Choice Questions and Answers.

« Prev - Class 8 Maths MCQ – Mensuration – Area of Trapezium – 2

» Next - Class 8 Maths MCQ – Mensuration – Surface Area of a Cube, Cuboid and Cylinder

Related Posts:

Recommended Articles: