This set of Class 8 Maths Chapter 10 Multiple Choice Questions & Answers (MCQs) focuses on “Visualising Solid Shapes”. These MCQs are created based on the latest CBSE syllabus and the NCERT curriculum, offering valuable assistance for exam preparation.
1. Name all the adjacent angles of the given quadrilateral.
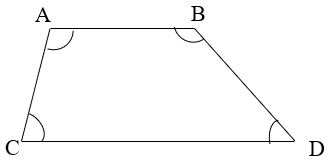
a) ∠A, ∠C; ∠B, ∠D
b) ∠A, ∠C
c) ∠A, ∠B; ∠B, ∠D; ∠D, ∠C; ∠C, ∠A
d) ∠A, ∠B; ∠A, ∠D
View Answer
Explanation: Two angles of a quadrilateral which have a common side as an arm are called adjacent angles. ∠A, ∠B; ∠B, ∠D; ∠D, ∠C; ∠C, ∠A are the adjacent angles of the given quadrilateral.
2. Which of the following are the opposite angles of the given quadrilateral?
a) ∠Q, ∠S; ∠Q, ∠P; ∠R, ∠S; ∠R, ∠P
b) ∠Q, ∠R; ∠P, ∠S
c) ∠Q, ∠P
d) ∠Q, ∠P; ∠S, ∠R
View Answer
Explanation: Two angles of a quadrilateral which are not adjacent angles are opposite angles.
∠A, ∠C; ∠B, ∠D are the opposite angles of the quadrilateral.
3. Match the following:
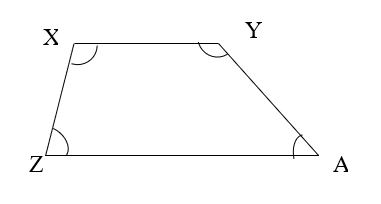
A B 1. Adjacent angles a. ∠X, ∠Y 2. Opposite angle b. ∠Y, ∠Z c. ∠A, ∠Y d. ∠A, ∠X
a) 1-a, c; 2-b, d
b) 1-a, b; 2-c, d
c) 1-a, b, c; 2-d
d) 1-a; 2-b, c, d
View Answer
Explanation: When two angles of a quadrilateral have a common side as an arm, they are called adjacent angles and the non-adjacent angles of a quadrilateral are opposite angles.
4. Match the following:
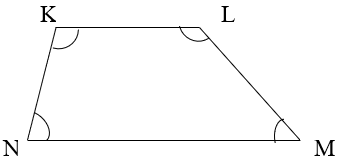
A B
1. Adjacent sides a. KL, LM
2. Opposite sides b. KL, MN
c. KN, LM
d. MN, NK
a) 1-b, c; 2-a, d
b) 1-b, d; 2-a, c
c) 1-a, b; 2-c, d
d) 1-a, d; 2-b, c
View Answer
Explanation: Two sides of a quadrilateral having a common end point are called adjacent sides of the quadrilateral. Two sides of a quadrilateral which are not having a common end point are called opposite sides of the quadrilateral.
5. Match the pairs:
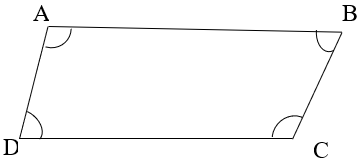
A B 1. Adjacent sides a. ∠D, ∠B 2. Opposite Angle b. AB, DA 3. Opposite Side c. ∠D, ∠C 4. Adjacent Angle d. AB, DC
a) 1-c, 2-a, 3-d, 4-b
b) 1-b, 2-c, 3-d, 4-a
c) 1-b, 2-a, 3-d, 4-c
d) 1-c, 2-a, 3-d, 4-b
View Answer
Explanation: Two sides of a quadrilateral having a common end point are called adjacent sides of the quadrilateral. Two sides of a quadrilateral which are not having a common end point are called opposite sides of the quadrilateral. Two angles of a quadrilateral which have a common side as an arm are called adjacent angles. Two angles of a quadrilateral which are not adjacent angles are opposite angles.
6. Which are the interior and exterior points of the quadrilateral?
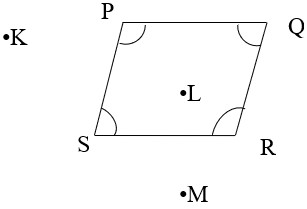
a) Interior point: L, Exterior point: M
b) Interior Point: P, Exterior point: O
c) Interior point: O, Exterior point: K
d) Interior point: L, Exterior point: O
View Answer
Explanation: Points inside the quadrilateral are called interior points of the quadrilateral. Points outside the quadrilateral are called the exterior points of the quadrilateral.
7. Find ∠B using the information given in the figure.
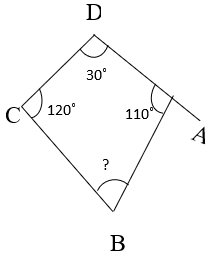
a) 10°
b) 100°
c) 110°
d) 50°
View Answer
Explanation: By Angle sum property of Quadrilateral,
∠A + ∠B + ∠C + ∠D = 360°
⇒ 110° + ∠B + 120° + 30° = 360°
⇒ ∠B = 100°.
8. If ∠P + ∠Q = 240 and ∠R = 90, find the remaining angle of the quadrilateral PQRS.
a) 30°
b) 40°
c) 50°
d) 60°
View Answer
Explanation: By Angle sum property of Quadrilateral,
∠P + ∠Q + ∠R + ∠S = 360°
240° + 90° + ∠S = 360°
⇒ ∠S = 30°.
9. Find the value of ∠O from the given figure.
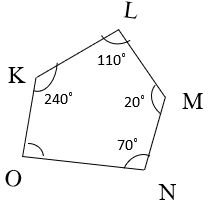
a) 110°
b) 30°
c) 90°
d) 100°
View Answer
Explanation: Sum of interior angles of a pentagon is 540°
⇒ ∠K + ∠L + ∠M + ∠N + ∠O = 540°
⇒ ∠O = 540° – 440°
⇒ ∠O = 100°.
10. Find the remaining angle of the given figure.
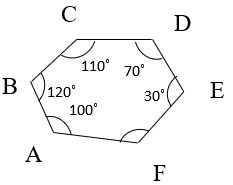
a) 260°
b) 270°
c) 300°
d) 290°
View Answer
Explanation: Sum of interior angles of a hexagon is 720°
⇒ ∠A + ∠B + ∠C + ∠D + ∠E + ∠F = 720°
⇒ ∠F = 720° – 43°
⇒ ∠F = 290°.
To practice all chapters and topics of class 8 Mathematics, here is complete set of 1000+ Multiple Choice Questions and Answers.
- Practice Class 9 Mathematics MCQs
- Practice Class 10 Mathematics MCQs
- Check Class 8 - Mathematics Books
