Area of Trapezium - Class 8 Maths MCQ

This set of Class 8 Maths Chapter 11 Multiple Choice Questions & Answers (MCQs) focuses on “Mensuration – Area of Trapezium – 2”.

1. Find the area of the given figure. (π = 3.14)

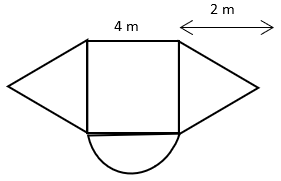
a) 30.28m²
b) 13.28m²
c) 26.28m²
d) 27.28m²
View Answer

Answer: a
Explanation: Area of the given figure = Area of square + semicircle + 2 × triangle
= (4)² + π \(\frac{(2)^2}{2} + 2 × \frac{1}{2}\) × 4 × 2 = 30.28m².

2. What is the area of the given figure? (π = \(\frac{22}{7}\))

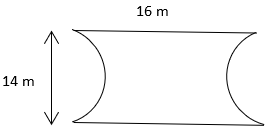
a) 70m²
b) 35m²
c) 74m²
d) 60m²
View Answer

Answer: a
Explanation: Area = Area of rectangle – Area of circle = l × b – π(r)² = 16 × 14 – \(\frac{22}{7}\) (7)² = 70m².

3. Find the area and perimeter of the given trapezium, respectively.

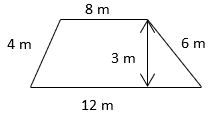
a) 30m², 15m
b) 15m², 30m
c) 15m², 15m
d) 30m², 30m
View Answer

Answer: d
Explanation: Area of trapezium = \(\frac{1}{2}\) × (p₁ + p₂) × h [(p₁ + p₂) = Σ of ∥sidesoftrapezium]
= \(\frac{1}{2}\) × (8 + 12) × 3 = 30m²
Perimeter = 4 + 8 + 6 + 12 = 30m.

4. Calculate the area of the given figure.

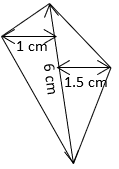
a) 7cm²
b) 7.5cm²
c) 6.5cm²
d) 8cm²
View Answer

Answer: b
Explanation: Area of general quadrilateral = \(\frac{1}{2}\) × (h₁ + h₂) × d [d is the length of diagonal]
= \(\frac{1}{2}\) × (1 + 1.5) × 6 = 7.5cm².

5. The Area of trapezium shaped garden is 225m². The distance between the two parallel sides is 25m. The length of one parallel side is 11m, what is the length of the other parallel side?
a) 7m
b) 8m
c) 6m
d) 5m
View Answer

Answer: a
Explanation: Area of trapezium = \(\frac{1}{2}\) × (p₁ + p₂) × h [(p₁ + p₂) = Σ of ∥ sidesoftrapezium]
⇒ 225m² = \(\frac{1}{2}\) × (11 + p₂) × 25
⇒ p₂ = 7m.

Sanfoundry Certification Contest of the Month is Live. 100+ Subjects. Participate Now!

6. The Area of trapezium is 800m². The lenghts of the parallel sides is 28mand 12m. Find the height of the trapezium.
a) 22m
b) 42m
c) 40m
d) 20m
View Answer

Answer: c
Explanation: Area of trapezium = \(\frac{1}{2}\) × (p₁ + p₂) × h [(p₁ + p₂) = Σ of ∥ sidesoftrapezium]
⇒ 800m² = \(\frac{1}{2}\) × (28 + 12) × h
⇒ h = 40m.

7. In a trapezium shaped ground, there is a square shaped lawn. The side of the lawn is 12m. The length of the parallel sides is 24m and 40m.The height of the ground is 30m. Find the area of the shaded portion.

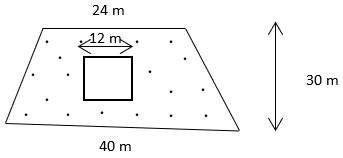
a) 806m²
b) 336m²
c) 1776m²
d) 816m²
View Answer

Answer: d
Explanation: Area of the shaded portion = Area of trapezium(ground) – Area of square(lawn)
= \(\frac{1}{2}\) × (p₁ + p₂) × h – (s)² = \(\frac{1}{2}\) × (40 + 24) × 30 – (12)² = 816m².

8. Find the area of the given Figure.

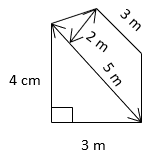
a) 42m²
b) 24m²
c) 14m²
d) 7m²
View Answer

Answer: c
Explanation: Area = Area of trapezium + Area of triangle = \(\frac{1}{2}\) × (p₁ + p₂) × h + \(\frac{1}{2}\) × b × h
= \(\frac{1}{2}\) × (5 + 3) × 2 + \(\frac{1}{2}\) × 4 × 3 = 14cm².

9. What is the area of the given figure?

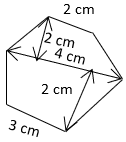
a) 10cm²
b) 13cm²
c) 12cm²
d) 11cm²
View Answer

Answer: b
Explanation: Area = Area of trapezium 1 + Area of trapezium 2
= \(\frac{1}{2}\) × (p₁ + p₂) × h₁ + \(\frac{1}{2}\) × (p₃ + p₄) × h₂ = \(\frac{1}{2}\) × (2 + 4) × 2 + \(\frac{1}{2}\) × (3 + 4) × 2 = 13cm².

10. Find length of AE if area of the given figure is 15cm².

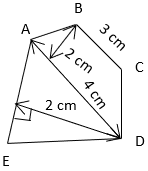
a) 9 cm
b) 8 cm
c) 7 cm
d) 6 cm
View Answer

Answer: b
Explanation: Area of given figure = Area of trapezium + Area of triangle
⇒ 15cm² = \(\frac{1}{2}\) × (p₁ + p₂) × h₁ + \(\frac{1}{2}\) × b × h
⇒ 15cm² = \(\frac{1}{2}\) × (4 + 3) × 2 + \(\frac{1}{2}\) × b × 2
⇒ b = 8 cm
⇒ length (AE) = 8 cm.

11. Compare the area of given trapezium.

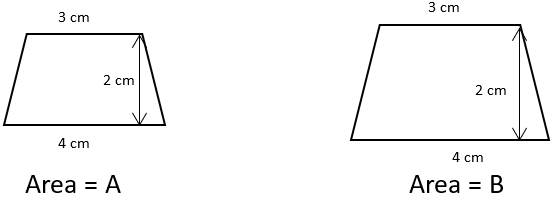
a) B > A
b) B < A
c) B = A = 7cm²
d) B = A = 9cm²
View Answer

Answer: a
Explanation: Area of A = \(\frac{1}{2}\) × (p₁ + p₂) × h₁ = \(\frac{1}{2}\) × (3 + 4) × 2 = 7cm²
Area of B = \(\frac{1}{2}\) × (p₁ + p₂) × h₁ = \(\frac{1}{2}\) × (3 + 4) × 2 = 7cm²
⇒ Area of B = Area of A.

Sanfoundry Global Education & Learning Series – Mathematics – Class 8.

To practice all chapters and topics of class 8 Mathematics, here is complete set of 1000+ Multiple Choice Questions and Answers.

If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]

« Prev - Class 8 Maths MCQ – Mensuration

» Next - Class 8 Maths MCQ – Mensuration – Area of General Quadrilaterals

Related Posts:

Recommended Articles: