This set of Bioseparation Processes Multiple Choice Questions & Answers (MCQs) focuses on “Single-Stage Continuous Extraction using Immiscible Solvents”.
1. What is the significance of the given diagram in the process of extraction in the bioseparation studies?
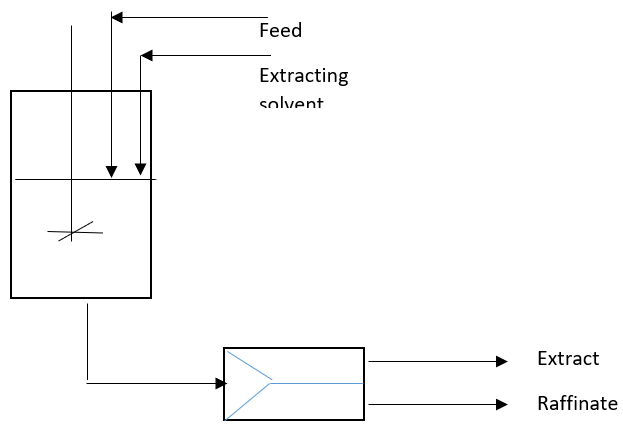
a) Single stage continuous extraction process
b) Multiple stage continuous extraction process
c) Single stage batch extraction process
d) Single stage fed-batch extraction process
View Answer
Explanation: The process of single stage continuous extraction process is the process of extraction which is considered to be the extended process of the batch extraction process. The process takes place in a single step which is a continuous process in the flow of feed and the release of extract as well as Raffinate from the extractor.
2. The feed and the extracting solvent streams enter the mixing unit continuously in the single stage continuous extraction process.
a) False
b) True
View Answer
Explanation: The transfer of solutes takes place in the mixing unit at a fixed resident time within the extractor and the process becomes sufficient for the completion of the extraction. Therefore, the flow of feed and the passing of extracting solvent in the extractor is continuous in the single stage continuous extraction process.
3. Which part of the step-up allows the phase extraction in the single stage continuous extraction process?
a) Within the extractor
b) Within the feed flow inlet
c) Within the settler unit
d) Within the outlet of the extract
View Answer
Explanation: The phase extraction takes place in the mixer of the single stage continuous extraction process and the emulsion produced in the mixer unit is fed in the settler unit and the Raffinate as well as the extracts are obtained through the stream.
4. What are the assumptions used in the analytical solution of single stage continuous extraction can be possible using the immiscible solvent system?
a) Exit stream not from the extractor
b) Negligible entrainment of other phase
c) Negligible entrainment of other phase, Exit stream not from the extractor
d) Exit stream is from the extractor, Negligible entrainment of other phase
View Answer
Explanation: The two assumptions of the analytical solution of the single stage continuous extraction process are presence of exit stream from the extractor in which the Raffinate as well as the extract are at the equilibrium and the negligible entrainment of any other phase which have exit stream for both the phases.
5. Which equation can be obtained from combining the equilibrium as well as the material balance relationship?
a) CE = –\(\frac{KC_{R0}}{1 + \lambda}\)
b) CE = \(\frac{K – C_{R0}}{1 + \lambda}\)
c) CE = \(\frac{KC_{R0}}{1 + \lambda}\)
d) CE = \(\frac{-KC_{R0}}{1 + \lambda}\)
View Answer
Explanation: The equation obtained from combination of material balance and the equilibrium relationship is CE = \(\frac{K – C_{R0}}{1 + \lambda}\) where, CE is the concentration of extract, K is the equilibrium constant, CR0 is the concentration of initial Raffinate.
6. What will be the final concentration of Raffinate in the single stage continuous extraction process?
a) CR = \(\frac{C_{R0}}{1 + \lambda}\)
b) CR = \(\frac{-C_{R0}}{1 + \lambda}\)
c) CR = –\(\frac{C_{R0}}{1 + \lambda}\)
d) CR = \(\frac{C_{R0}}{1 – \lambda}\)
View Answer
Explanation: The final concentration of Raffinate is CR = \(\frac{C_{R0}}{1 + \lambda}\) in the single stage continuous extraction process in the presence of immiscible liquid. In the equation, λ is the extraction factor used for the process of extraction and CR0 is the initial concentration of Raffinate fed in the stream.
7. What is the equation for the extraction factor for the single stage continuous extraction system?
a) λ = \(\frac{K-Q_E}{Q_R}\)
b) λ = –\(\frac{KQ_E}{Q_R}\)
c) λ = \(\frac{KQ_E}{-Q_R}\)
d) λ = \(\frac{KQ_E}{Q_R}\)
View Answer
Explanation: The extraction factor of the single stage continuous extraction can be obtained using equation λ = \(\frac{KQ_E}{Q_R}\) where, K is the equilibrium constant, QE is the flow rates of the extracting solvents, QR is the flow rate of the initial solvent in the feed.
8. What is the operating line for the methods used in the single stage continuous extraction process?
a) CE = -(\(\frac{Q_R}{Q_E})\)(CR0 – CR)
b) CE = (\(\frac{Q_R}{Q_E})\) – (CR0 – CR)
c) CE = (\(\frac{Q_R}{Q_E})\)(CR0 – CR)
d) CE = (\(\frac{Q_R}{Q_E})\)(CR0 + CR)
View Answer
Explanation: The operating line for the methods in the single stage continuous system in the extraction process is CE = (\(\frac{Q_R}{Q_E})\)(CR0 – CR), which is the equilibrium function of the system and it is the non-linear method of representation.
9. Calculate the concentration of the chemical in the extract as well as Raffinate when the broth entered a mixing setup at continuous extraction unit with 100 l/min flow rate having 20g/l of a chemical and pH is 3. The acid is entering the extractor at 10l/min flow rate. Given: CE = 40 CR.
a) 160 g/l, 4 g/l
b) 4g/l, 160g/l
c) 150g/l, 5 g/l
d) 5g/l, 150 g/l
View Answer
Explanation: The separation of the chemical follows a mass balance equation and it is (100 × 20) = 100 QR + 10 QL and the given equilibrium relation is CE = 40 CR therefore, after calculation the obtained values are CE = \(\frac{160g}{l}\) and CR = 4 \(\frac{g}{l}\).
10. Calculate the fraction of the chemical when, CE = \(\frac{160g}{l}\) and CR = 4 \(\frac{g}{l}\) 100 l/min flow rate having 20g/l of a chemical entering a mixing unit at continuous extraction unit in which the acid entered in the extractor at 10l/min flow rate.
a) 0.5
b) 0.6
c) 0.7
d) 0.8
View Answer
Explanation: The fraction of the chemical extracted at the first stage is
p = \(\frac{flow\, rate\, of\, acid\, × \,concentration\, of\, extract}{flow\, rate\, of\, broth\,
× \,flow\, rate\, of\, chemical} = \frac{10 × 160}{100 × 20}\) = 0.8.
11. Calculate the concentration of the chemical in the extract as well as Raffinate in the second phase, when the organic extract from the first extraction step has entered the second mixing unit and the feed flow rate was 5 l/min. Given: the equilibrium relationship is given by CE = 37 CR.
a) 303.6 g/l, 2 g/l
b) 303.6g/l, 8.205 g/l
c) 2g/l, 8.205g/l
d) 8.39g/l, 24g/l
View Answer
Explanation: The separation of the chemical follows a mass balance equation for the second phase and it is (10 × 160) = 10 CR + 5 CE and the given equilibrium relation is CE = 37CR therefore, after calculation the obtained values are CE = 303.6 \(\frac{g}{l}\) and CR = 8.205 \(\frac{g}{l}\).
12. Calculate the fraction of the chemical which can be extracted when, CE = \(\frac{303.6 g}{l}\) and CR = 8.205 \(\frac{g}{l}\). The organic extract from the first extraction step enters a second continuous mixer settler extraction unit and the fed flow rate was 5 l/min.
a) 0.559
b) 0.659
c) 0.759
d) 0.859
View Answer
Explanation: The fraction of the chemical extracted at the first stage is
p = \(\frac{flow\, rate\, of\, acid\, × \,concentration\, of\, extract}{flow\, rate\, of\, broth\,
× \,flow\, rate\, of\, chemical} = \frac{5 × 303.6}{100 × 20}\) = 0.759.
Sanfoundry Global Education & Learning Series – Bioseparation Processes.
To practice all areas of Bioseparation Processes, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
