This set of Bioseparation Science Multiple Choice Questions & Answers (MCQs) focuses on “Shape and Yield of a Chromatographic Peak”.
1. Which theory predicts the chromatographic elution peak approximate to distribution related to Poisson distribution?
a) Plate theory
b) Point theory
c) Peak theory
d) Flow theory
View Answer
Explanation: The plate theory is used for prediction of a chromatographic elution peak that would be approximately distributed to a Poisson distribution. The large number of plates can be further simplified in a different form through Gaussian theory.
2. The yield from the approximation of the Poisson distribution can be expressed through ___
a) mobile phase peak
b) stationary phase peak
c) solute flow rate
d) concentration profile peak
View Answer
Explanation: C = C0 exp( –\(\frac{(t – t_0 )^2}{2\sigma^2}\)) is the expression for the concentration profile peak where C0 is the maximum concentration of solute, t0 is the maximum time taken by
the solute to reach that concentration, σ2 is the varance of the associated peak, which expresses the yield to work with.
3. The characteristic peak width is equal to ___
a) 1σ
b) 3σ
c) 4σ
d) 6σ
View Answer
Explanation: The characteristic peak width is equal to 4σ. The initial time is the same as tR and is expressed in terms of concentration profile peak.
4. What is the significance of the given diagram?
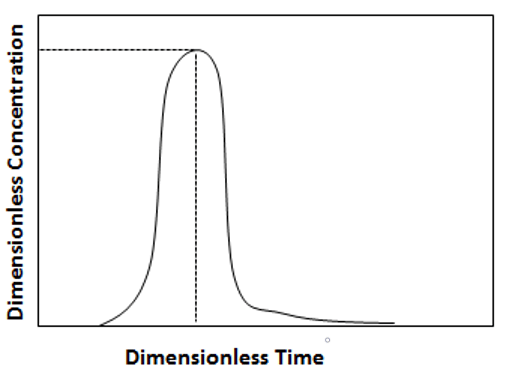
a) Dimensional plot
b) Dimensionless plot
c) Chromatographic peak of time
d) Time profile
View Answer
Explanation: The peaks represents the dimensionless quantities and it expresses the concentration of the solute flow with time making it a chromatographic peak based on the flow of sample through the column.
5. Which terms in the above plot expresses the dimensionless measurements?
a) Concentration
b) Time
c) Concentration and time
d) Flow rate
View Answer
Explanation: The Concentration of the solute is the dimensionless quantity i.e. C/C0 and the time taken by the solute to cross the column and get eluted i.e. t/t0 is the dimensionless quantity.
6. The amount of solute eluted in a peak is given by ___
a) Mtotal = -Q\(\int_0^\infty\) Cdt
b) Mtotal = Q\(\int_0^\infty\) – Cdt
c) Mtotal = Q\(\int_0^\infty\) dCdt
d) Mtotal = Q\(\int_0^\infty\) Cdt
View Answer
Explanation: The equation for the representation of elution of solute is Mtotal = Q\(\int_0^\infty\) Cdt where, Mtotal is the total amount of solute shown in the peak, Q is the rate of flow of mobile phase.
7. The percentage yield of the solute can be represented through ___
a) % yield = \([\frac{\int_{t2}^{t1}Cdt}{\int_0^\infty Cdt}]\) × 100
b) % yield = \([-\frac{\int_{t2}^{t1}Cdt}{\int_0^\infty Cdt}]\) × 100
c) % yield = \([\frac{\int_{t2}^{t1}Cdt}{\int_0^\infty Cdt}]\) × 10
d) % yield = \(\frac{\int_{t2}^{t1}Cdt}{\int_0^\infty dCdt}]\) × 100
View Answer
Explanation: The yield %age can be given by \(\frac{\int_{t2}^{t1}Cdt}{\int_0^\infty Cdt}\) × 100 where, purity of separation of solutes can be collected from the effluents in the given time period.
8. What will be the % purity of a solute?
a) % purity = \([\frac{\int_{t1}^{t2} CAdt}{\int_{t1}^{t2} CAdt + \int_{t1}^{t2} CBdt}] \) × 100
b) % purity = \([\frac{\int_{t2}^{t1}Cdt}{\int_0^\infty Cdt}]\) × 100
c) % purity = \([\frac{\int_{t1}^{t2} – CAdt}{\int_{t1}^{t2} CAdt + \int_{t1}^{t2} CBdt}] \) × 100
d) % purity = \([\frac{\int_{t1}^{\infty} CAdt}{\int_{t1}^{t2} CAdt + \int_{t1}^{t2} CBdt} ]\) × 100
View Answer
Explanation: % purity = [ \(\frac{\int_{t1}^{t2} CAdt}{\int_{t1}^{t2} CAdt + \int_{t1}^{t2} CBdt} \) ] × 100 for the samples A and B in the binary separation of solutes that is collected in the time period of initial and final time.
9. What is the height of theoretical plate of the column used in chromatography when the injecting pore is 30cm long? (Given: width of peak is 4min and initial time is 5min and number of theoretical plates is 25).
a) 1.3cm
b) 1.2cm
c) 1.25cm
d) 1.4cm
View Answer
Explanation: Height (H) is the ratio of injecting pore and the number of plates.
H = \(\frac{Injecting\, pore\, length}{number\, of\, theoretical\, plate} = \frac{30}{25}\) = 1.2cm.
10. Calculate the % purity of the solute in the sample when the initial time is 0 and final time is 7min. Given: CA = \(\frac{5g}{l}\), CB = \(\frac{10g}{l}\).
a) 75%
b) 76%
c) 78%
d) 78.5%
View Answer
Explanation: % purity = [ \(\frac{\int_{t1}^{t2} CAdt}{\int_{t1}^{t2} CAdt + \int_{t1}^{t2} CBdt} \) ] × 100 = [ \(\frac{\int_0^7 \frac{5g}{l}}{\int_0^7 \frac{5g}{l} + \int_0^7 \frac{10g}{l}}\) ] × 100 = 78.5%.
Sanfoundry Global Education & Learning Series – Bioseparation Science.
To practice all areas of Bioseparation Science, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
