This set of Class 9 Maths Chapter 10 Multiple Choice Questions & Answers (MCQs) focuses on “Circles – Equal Chords and their Distances from the Centre”.
1. What is the length of AB if CD = 8cm?
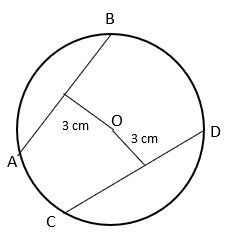
a) 5 cm
b) 8 cm
c) 4 cm
d) 2 cm
View Answer
Explanation: Chords which are equidistant from centre of a circle are equal in length. Hence, AB = CD = 8 cm.
2. Find the value of x if O is the centre of circle?
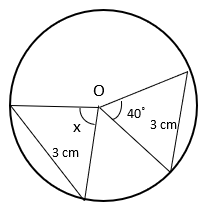
a) 20°
b) 45°
c) 90°
d) 40°
View Answer
Explanation: Equal chords subtend equal angles at the centre. As the chords are of same length of 3cm, x = 40°.
3. Find the value of ∠QOR if O is the centre of circle.
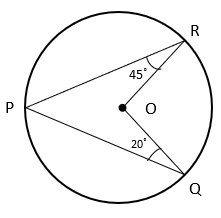
a) 50°
b) 65°
c) 130°
d) 30°
View Answer
Explanation: Join OP
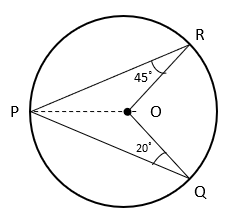
In ΔPOQ, OP = OQ [Radii of same circle]
⇒ ∠OPQ = ∠OQP = 20° [Angles opposite to equal sides are equal]
In ΔPOR, OP = OR [Radii of same circle]
⇒ ∠OPR = ∠ORP = 45° [Angles opposite to equal sides are equal]
Now, ∠QPR = ∠OPR + ∠OPQ = 45° + 20° = 65°
Angle subtended by an arc of circle at the centre is twice the angle subtended by the arc on circumference ⇒ ∠ROQ = 2∠QPR = 2 x 65° = 130°.
4. Find the value of ∠ABC if O is the centre of circle.
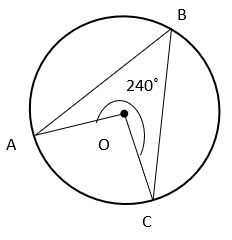
a) 60°
b) 120°
c) 240°
d) 180°
View Answer
Explanation: Reflex ∠AOC = 240°
⇒ ∠AOC = 360° – Reflex ∠AOC = 360° – 240° = 120°
Since angle subtended by an arc of circle at the centre is twice the angle subtended by the arc on circumference, ∠AOC = 2∠ABC
⇒ ∠ABC = ½ ∠AOC = 60°.
5. What is the value of ∠PRQ if angle POQ and reflex angle POQ are in the ratio 1 : 3?
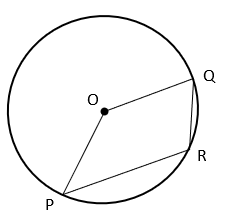
a) 135°
b) 50°
c) 115°
d) 80°
View Answer
Explanation: From figure, Angle around a point is 360° ⇒ ∠POQ + Reflex ∠POQ = 360°
⇒ x + 3x = 360° ⇒ x = 90°
Hence, Reflex ∠POQ = 3x = 270°
Since angle subtended by an arc of circle at the centre is twice the angle subtended by the arc on circumference, Reflex ∠POQ = 2∠PRB
⇒ ∠PRB = ½ x 270° = 135°.
6. Find the value of ∠PRQ from the given figure.
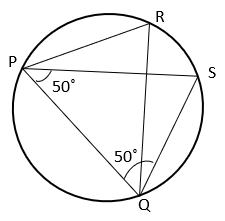
a) 50°
b) 160°
c) 80°
d) 30°
View Answer
Explanation: In ΔPSQ, ∠PSQ + ∠SPQ + ∠SQP = 180° [Angle sum property of triangle]
⇒ ∠PSQ + 50° + 50° = 180°
⇒ ∠PSQ = 80°
Angles subtended by an arc in the same segment are equal ⇒ ∠PRQ = ∠PSQ = 80°.
7. What is the value of ∠PRQ if ∠PTS : ∠TPS = 5 : 3?
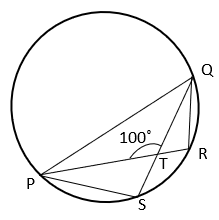
a) 66°
b) 54°
c) 30°
d) 45°
View Answer
Explanation: From figure, ∠PTQ + ∠PTS = 180° [Linear Pair]
⇒ ∠PTS = 80°
In ΔPTS, ∠PST + ∠TPS + ∠PTS = 180° [Angle sum property of triangle]
⇒ ∠PST + 80° + 3/5 x 80° = 180° [∠PTS : ∠TPS = 5 : 3]
⇒ ∠PST = 54°
Since angles subtended by an arc in the same segment are equal, ∠PRQ = ∠PSQ = 54°.
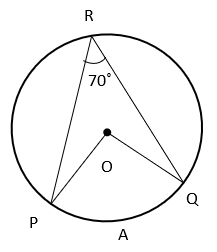
8. Find the measure of arc PAQ.
a) 90°
b) 50°
c) 70°
d) 140°
View Answer
Explanation: Measure of an arc is angle subtended by it at the centre of circle.
⇒ m(PAQ) = ∠POQ
But, ∠POQ = 2∠PRQ [Angle subtended by an arc of circle at the centre is twice the angle subtended by the arc on circumference]
Hence, m(PAQ) = ∠POQ = 2∠PRQ = 140°.
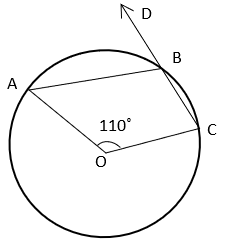
9. What is the value of x if O is the centre of circle?
a) 90°
b) 110°
c) 70°
d) 55°
View Answer
Explanation: As angle subtended by an arc of circle at the centre is twice the angle subtended by the arc on circumference, ∠ABC = ½ reflex ∠AOC = ½ (360° – 110°) = 125°.
Now, ∠ABD + ∠ABC = 180° [Linear Pair]
⇒ x = 180° – 120° = 55°.
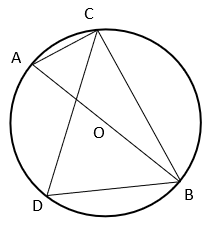
10. What is the value of ∠BDC if ∠BAC: ∠ABC = 4 : 5 and O is the centre of circle?
a) 40°
b) 10°
c) 90°
d) 55°
View Answer
Explanation: In ΔABC, ∠ACB = 90° as angle in a semicircle is right angle.
Also, ∠BAC = 4k and ∠ABC = 5k
Now, ∠ACB + ∠ABC + ∠BAC = 180° [Angle sum property of triangle]
⇒ 90° + 4k + 5k = 180°
⇒ k = 10°
⇒ ∠BAC = 4k = 40°
Since angles subtended by an arc in the same segment are equal, ∠BDC = ∠BAC = 40°.
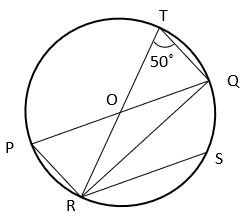
11. Find the value of ∠QRS if RS || diameter PQ.
a) 90°
b) 15°
c) 40°
d) 20°
View Answer
Explanation: From figure, ∠PRQ = 90° as angle in a semicircle is right angle.
Also, ∠RPQ = ∠RTQ = 50° [angles subtended by an arc in the same segment are equal]
Now, in ΔPQR, ∠PRQ + ∠QPR + ∠PQR = 180° [Angle sum property of triangle]
⇒ 90° + 50° + ∠PQR = 180°
⇒ ∠PQR = 40°
Now, PQ || RS ⇒ ∠PQR = ∠QRS [Alternate interior angles]
⇒ ∠QRS = 40°.
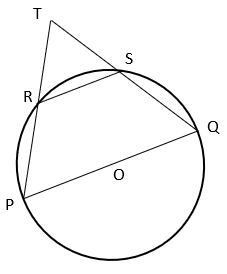
12. If RS is equal to the radius of circle, find the value of ∠PTQ.
a) 90°
b) 60°
c) 45°
d) 30°
View Answer
Explanation: Join OS, OR and RQ
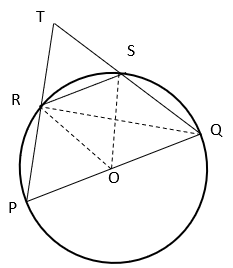
From figure, ∠PRQ = 90° as angle in a semicircle is right angle.
Now, ∠QRT = 180° – ∠PRQ [Linear Pair]
⇒ ∠QRT = 180° – 90° = 90° ————–(i)
In ΔROS, OS = OR = RS ⇒ ΔROS is an equilateral triangle.
⇒ ∠ROS = 60°
Now, ∠SQR = ½ ∠ROS [angle subtended by an arc of circle at the centre is twice the angle subtended by the arc on circumference]
⇒ ∠SQR = 30° —————-(ii)
In ΔTQR, ∠TRQ + ∠QTR + ∠TQR = 180° [Angle sum property of triangle]
⇒ 90° + ∠PQR + 30° = 180° [from equation i and ii]
⇒ ∠PQR = 60°.
Sanfoundry Global Education & Learning Series – Mathematics – Class 9.
To practice all chapters and topics of class 9 Mathematics, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
- Practice Class 10 Mathematics MCQs
- Practice Class 8 Mathematics MCQs
- Check Class 9 - Mathematics Books
