This set of Class 10 Maths Chapter 10 Multiple Choice Questions & Answers (MCQs) focuses on “Circles”. These MCQs are created based on the latest CBSE syllabus and the NCERT curriculum, offering valuable assistance for exam preparation.
1. Identify the parts of a circle.
a) Sides
b) Chord
c) Corners
d) Faces
View Answer
Explanation: Chord is one of the parts of a circle. A line segment that joins any two points on a circle is called a chord. The other parts of a circle are arc, segment, secant, radius, diameter, etc.
2. Choose the correct statement.
a) The center of the circle belongs to the circle
b) The angle in a semi-circle is a complete angle
c) A circle can have only two parallel tangents
d) Radius equals to twice of the diameter
View Answer
Explanation: A circle can have only two parallel tangents. These two parallel tangents touch either end of the diameter. Hence, ‘A circle can have only two parallel tangents’ is the only correct statement.
3. The angle in a semi-circle is _____
a) 90°
b) 180°
c) 0°
d) 360°
View Answer
Explanation: The angle in a semi-circle is 180° whereas the angle in a circle is a complete angle that is 360° and an angle is said to be 0° when the circle is in the form of a point.
4. Length of the tangent is _____
a) \(\sqrt {d^2+c^2}\)
b) \(\sqrt {r^2-d^2}\)
c) \(\sqrt {d^2-c^2}\)
d) \(\sqrt {d^2-r^2}\)
View Answer
Explanation: Length of the tangent (l) = \(\sqrt {d^2-r^2}\)
Where, l = Length of the tangent.
d = Distance between center of the circle and the external point of the circle.
r = Radius of the circle.
5. The line intersecting a circle at exactly one point is called as _____
a) arc
b) secant
c) chord
d) tangent
View Answer
Explanation: A line that touches/intersects a circle at exactly one point of a circle is called a tangent and an infinite number of tangents are drawn to a circle whereas secant is a line that intersects two distinct points on a circle.
6. What is the name of the point which is common to circle and the tangent?
a) Intersection point
b) Tangential point
c) Point of contact
d) Point of touch
View Answer
Explanation: A line that touches/intersects a circle at exactly one point of a circle is called a tangent and the point which is common for both circle and tangent is called the point of contact.
7. The radius is always _____ to the tangent.
a) equal
b) perpendicular
c) twice
d) parallel
View Answer
Explanation: Radius is measured from the center of the circle to any point on the circle and it is always perpendicular to the tangent drawn at their common point of contact.
8. Find the length of the tangent if d = 5 cm and r = 4 cm.
a) 3 cm
b) 4 cm
c) 5 cm
d) 9 cm
View Answer
Explanation: The length of the tangent = \(\sqrt {d^2-r^2}\)
= \(\sqrt {5^2-4^2}\)
= √9
= 3
9. Find the radius of a circle if 8 m is the length of the tangent, 11 m is the distance between the center of the circle the external point.
a) 7 m
b) 5 m
c) √57 m
d) √58 m
View Answer
Explanation: Length of the tangent = \(\sqrt {d^2-r^2}\)
8 = \(\sqrt {11^2-r^2}\)
r2 = 112 – 82
r = \(\sqrt {11^2-8^2}\)
r = \(\sqrt {121-64}\)
r = √57
10. Identify the tangents in the circle.
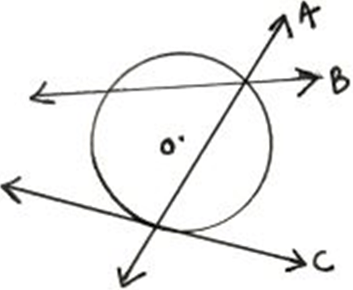
a) Only A
b) A and B
c) Only C
d) A and C
View Answer
Explanation: The line only C is the tangent of the given circle because line C is the only line that touches the given circle at only a single point and the lines A, B are the secants of the circle because they touch the circle in two distinct points.
11. Identify the secants in the circle.

a) Only A
b) A and B
c) Only C
d) A and C
View Answer
Explanation: The lines A and B are the secants of the circle because they touch the circle in two distinct points whereas line C is the only tangent of the circle because it intersects the circle at only a single point.
12. Identify the type of tangents.
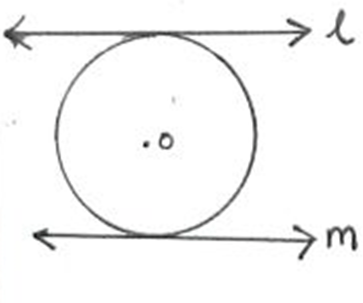
a) Parallel tangents
b) Concurrent tangents
c) Perpendicular tangents
d) Equal tangents
View Answer
Explanation: The type of tangents l and m are parallel tangents because they both are parallel to each other and a circle can have only two parallel tangents.
13. Identify the type of tangents.
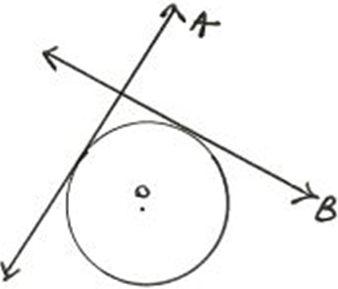
a) Parallel tangents
b) Concurrent tangents
c) Perpendicular tangents
d) Equal tangents
View Answer
Explanation: The type of tangents A and B are perpendicular tangents because they both are perpendicular to each other. The formation of 90° between both the tangents makes them a pair of perpendicular tangents.
14. Find the length of the tangent.
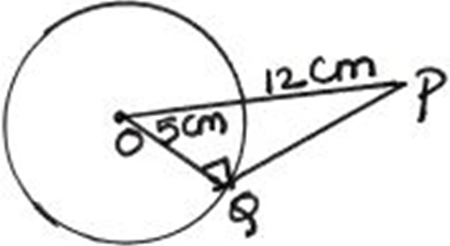
a) 10 cm
b) 11 cm
c) √197 cm
d) √199 cm
View Answer
Explanation: The length of the tangent = \(\sqrt {d^2-r^2}\)
= \(\sqrt {12^2-5^2}\)
= \(\sqrt {144-25}\)
= √199
15. Find the area of the circle if 8 cm is the length of the tangent, 11 cm is the distance between the center of the circle the external point.
a) 100 cm
b) 110 cm
c) 197.14 cm
d) 179.14 cm
View Answer
Explanation: Length of the tangent = \(\sqrt {d^2-r^2}\)
8 = \(\sqrt {11^2-r^2}\)
r2 = 112 – 82
r = \(\sqrt {11^2-8^2}\)
r = √57
Area of the circle = πr2
= \(\frac {22}{7}\)(√57)2
= 179.14
More MCQs on Class 10 Maths Chapter 10:
To practice all chapters and topics of class 10 Mathematics, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
- Check Class 10 - Mathematics Books
- Practice Class 8 Mathematics MCQs
- Practice Class 9 Mathematics MCQs
