This set of Class 9 Maths Chapter 6 Multiple Choice Questions & Answers (MCQs) focuses on “Parallel Lines and Transversal – 2”.
1. Match the following pairs.
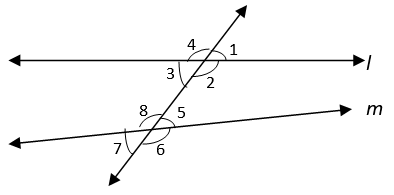
| A | B |
| i) ∠1 and ∠5 | I) Interior angles |
| ii) ∠4 and ∠ | II) Exterior Angles |
| iii) ∠3 and ∠5 | III) Corresponding Angles |
a) i-I, ii-II, iii-III
b) i-II, ii-I, iii-III
c) i-III, ii-I, iii-II
d) i-III, ii-II, iii-I
View Answer
Explanation: When a transversal intersects two lines, pair of angles are formed. ∠1 and ∠5, ∠2 and ∠6, ∠4 and ∠8, ∠3 and ∠7 are corresponding angles. ∠1 and ∠7, ∠4 and ∠6 are alternate exterior angles. ∠2 and ∠8, ∠3 and ∠5 are alternate interior angles. ∠2 and ∠5, ∠3 and ∠8 are interior angles on the same side of transversal.
2. Which of the following is not correct if l || m.
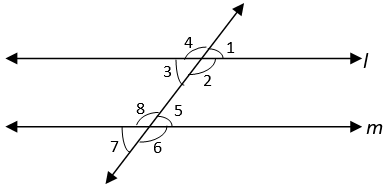
a) ∠1 = ∠5
b) ∠1 = ∠3
c) ∠1 = ∠7
d) ∠2 = ∠6
View Answer
Explanation: When a transversal intersects two parallel lines, corresponding pair of angles are equal. ∠1 = ∠5, ∠2 = ∠6, ∠4 = ∠8, ∠3 = ∠7 as they are corresponding angles. ∠1 and ∠3 are vertically opposite angles and are equal.
3. Find the value of x if p || q.
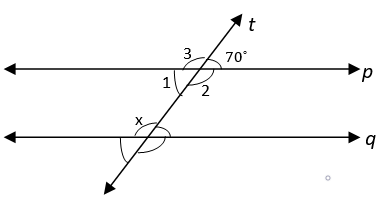
a) 110°
b) 360°
c) 140°
d) 80°
View Answer
Explanation: Line p || Line q and line t is transversal.
From figure, ∠1 = 70° (Vertically Opposite Angles)
Also, ∠1 + x = 180° (Sum of Interior Angles on the same side of transversal is 180°)
⇒ x = 180° – 70°
⇒ x = 110°
4. Find the value of k if p || q.
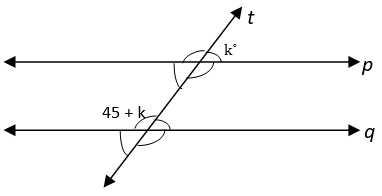
a) 10°
b) 60°
c) 67.5°
d) 80°
View Answer
Explanation: Line p || Line q and line t is transversal.
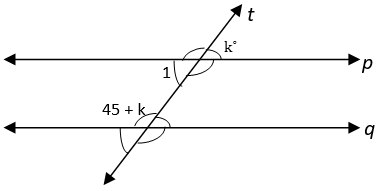
From figure, ∠1 = k° (Vertically Opposite Angles)
Also, ∠1 + (45 + k) = 180° (Sum of Interior Angles on the same side of transversal is 180°)
⇒ k + 45 + k = 180°
⇒ 2k = 180° – 45°
⇒ 2k = 135°
⇒ k = 67.5°
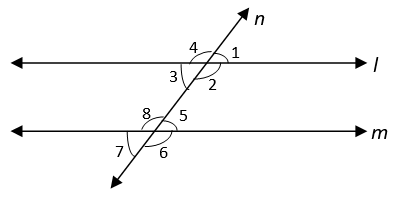
5. Find the value of ∠5 and ∠8 if l || m and ∠1 : ∠2 = 2 : 7.
a) 10°, 70°
b) 40°, 140°
c) 110°, 70°
d) 35°, 140°
View Answer
Explanation: Line l || Line m and line n is transversal and ∠1 : ∠2 = 2 : 7
From figure, ∠1 + ∠2 = 180° (Sum of Interior Angles on the same side of transversal is 180°)
⇒ 2k + 7k = 180°
⇒ 9k = 180°
⇒ k = 20°
⇒ ∠1 = 2k = 40° and ∠2 = 7k = 140°.
Now, ∠1 = ∠5 = 40° (Corresponding Angles)
and ∠2 = ∠8 = 140° (Alternate Interior Angles)
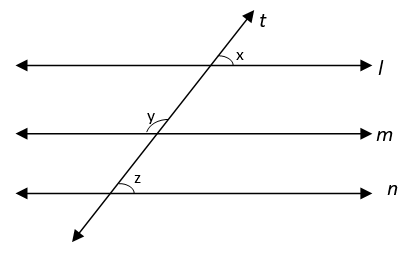
6. Find the value of x if l || m || n and y : z = 5 : 4.
a) 50°
b) 60°
c) 70°
d) 80°
View Answer
Explanation: Line l || Line m || Line n and line t is transversal and y : z = 5 : 4
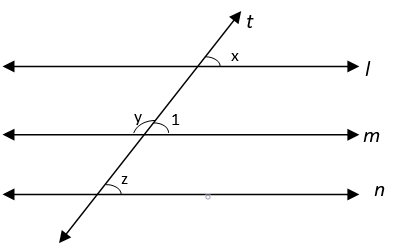
From figure, ∠1 = z (Corresponding Angles as Line m || Line n)
∠y + ∠z = 180° (Linear Pair)
⇒ 5k + 4k = 180°
⇒ 9k = 180°
⇒ k = 20°
⇒ ∠y = 5k = 100° and ∠z = 4k = 80°.
Now, ∠z = ∠x (Corresponding Angles as Line l || Line m)
⇒ x = 80°.
7. Find the value of ∠ABC if PQ|| RS.
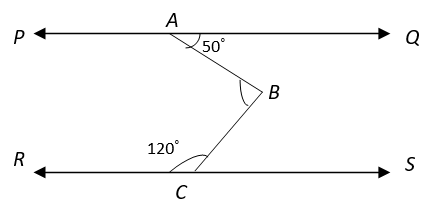
a) 70°
b) 140°
c) 110°
d) 90°
View Answer
Explanation: Line PQ|| RS. Draw a line passing through B and parallel to PQ and RS
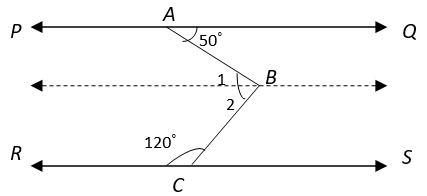
From figure, ∠1 = 50° (Alternate Interior Angles)
Also, 120° + ∠2 = 180° (Sum of Interior Angles on the same side of transversal is 180°)
⇒ ∠2 = 180° – 120° = 60°
Now, ∠ABC = ∠1 + ∠2
⇒ ∠ABC = 50° + 60°
⇒ ∠ABC = 110°.
Sanfoundry Global Education & Learning Series – Mathematics – Class 9.
To practice all chapters and topics of class 9 Mathematics, here is complete set of 1000+ Multiple Choice Questions and Answers.
