Parallelograms on the Same Base and Between the Same Parallels - Class 9 Maths MCQ

This set of Class 9 Maths Chapter 9 Multiple Choice Questions & Answers (MCQs) focuses on “Parallelograms & Triangles on the Same Base and Between the Same Parallels – 1”.

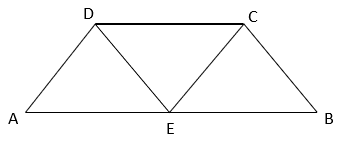
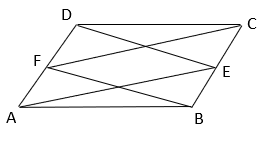
1. Which of the following figures are on the same base and between same parallels?
a)

b)

c)

d)

View Answer

Answer: a
Explanation: If two geometric figures have a common side and if the vertices opposite to common base of each figure lie on line parallel to base, they are said to be on same base and between same parallels. So, in only one figure, the above condition is satisfied.

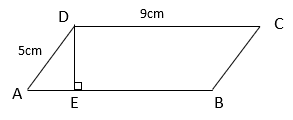
2. Find the area of parallelogram ABCD if AE : EB = 1 : 2.

a) 25 sqm
b) 22.5 sqm
c) 36 sqm
d) 45 sqm
View Answer

Answer: c
Explanation: In parallelogram ABCD, AB = CD = 9cm (Opposite sides of a parallelogram are equal)
Now, AE : EB = 1 : 2 and AE + EB = AB
⇒ k + 2k = 9 ⇒ k = 3
⇒ AE = 3cm
In ΔAED, AD² = AE² + ED² (By Pythagoras theorem)
⇒ 5² = 3² + ED²
⇒ ED² = 25 – 9 = 16
⇒ ED = 4cm
Now, Area of parallelogram ABCD = Base x corresponding altitude = AB x DE = 9 x 4 = 36sqm.

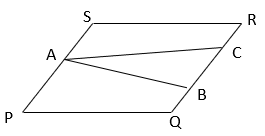
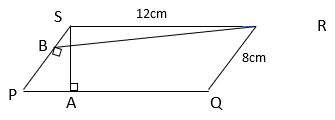
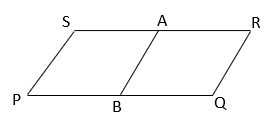
3. Find the value of BR from the following figure if ABCD is a parallelogram and AS = 6cm?

a) 5cm
b) 2cm
c) 6cm
d) 9cm
View Answer

Answer: d
Explanation: Area of a parallelogram = base x corresponding altitude
From figure, area of parallelogram PQRS = PS x BR = PQ x AS
⇒ 8 x BR = 12 x 6 ⇒ BR = 9cm.

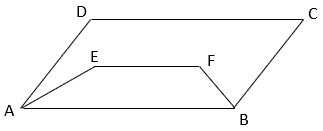
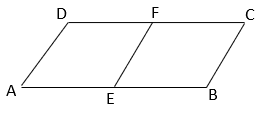
4. Find the ration of area of parallelogram AEFD to area of parallelogram EBCF if E and F are mid points of AB and CD respectively.

a) 1
b) 2
c) 4
d) 3
View Answer

Answer: a
Explanation: ABCD is a parallelogram.
⇒ AB || CD & AB = CD
⇒ AE || DF & ½ AB = ½ CD
⇒ AE || DF & AE = DF ⇒ AEDF is a parallelogram.
Similarly, EBCF is a parallelogram.
Now, AEDF and EBCF are parallelogram on equal bases and between same parallels, hence they have equal areas. ⇒ Area of parallelogram AEDF: Area of parallelogram EFBC = 1.

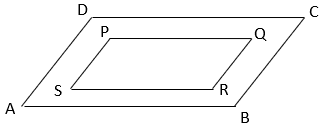
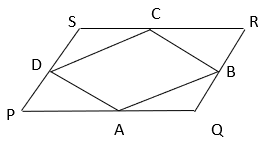
5. Find the ratio of area of parallelogram ABCD to area of parallelogram PQRS if A, B, C and D are mid points of parallelogram.

a) 1/2
b) 1
c) 2
d) 3
View Answer

Answer: a
Explanation: PQRS is a parallelogram.
⇒ PQ = RS & PS = RQ
⇒ ½ PQ = ½ RS & ½ PS = ½ RQ
⇒ PA = CS, PD = BQ, AQ = CR and DS = BR ——————- (i)
Now, PD = BQ and PD || BQ ⇒ PQBD is a parallelogram.
Parallelogram PQBD and triangle ABD are on same base BD and between same parallels PQ and BD ⇒ ar(ΔADE) = ½ ar(PQBD) ————— (i)
Similarly, since DS = RB and DS || RB, DBRS is a parallelogram.
Parallelogram DBRS and triangle BCD are on same base BD and between same parallels BD and RS ⇒ ar(∆BCD) = ½ ar(DBRS) ————— (ii)
Adding equation i and ii, ar(ΔADE) + ar(ΔBCD) = ½ ar(PQBD) + ½ ar(DBRS)
⇒ ar(ABCD) = ½ ar(PQRS).

Subscribe Now: Class 9 - Mathematics Newsletter | Important Subjects Newsletters

6. Which of following relation is correct if ABCD is a parallelogram?

a) ar(ADE) < ar(CDF)
b) ar(ADE) > ar(CDF)
c) ar(ADE) = ar(CDF)
d) ar(ADE) = ½ ar(CDF)
View Answer

Answer: c
Explanation: From figure, ΔADE and parallelogram ABCD are on same base AD and between same parallels AD and BC.
⇒ ar(ΔADE) = ½ ar(ABCD) ————— (i)
ΔDCF and parallelogram ABCD are on same base CD and between same parallels CD and AB.
⇒ ar(ΔCDF) = ½ ar(ABCD) ————— (ii)
From equation i and ii,
⇒ ar(ΔADE) = ar(ΔCDF).

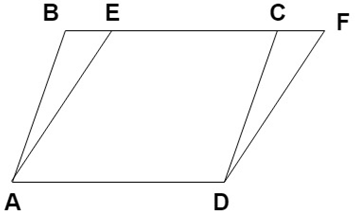
7. Find the area of parallelogram ABQR if area of parallelogram PQRS is 150sqm, A and B are midpoints of PQ and RS.

a) 100sqm
b) 300sqm
c) 150sqm
d) 75sqm
View Answer

Answer: d
Explanation: From figure, PQ || RS ⇒ BQ || AR
and PQ = RS ⇒ BQ = AR and BP = AS
Now, Area of parallelogram ABQR = Area of parallelogram PBAS ———— (i)
Area of parallelogram PQRS = Area of parallelogram ABQR + Area of parallelogram PBAS
⇒ Area of parallelogram PQRS = 2 x Area of parallelogram ABQR (from equation i)
⇒ Area of parallelogram ABQR = ½ x Area of parallelogram PQRS = ½ x 150 = 75sqm.

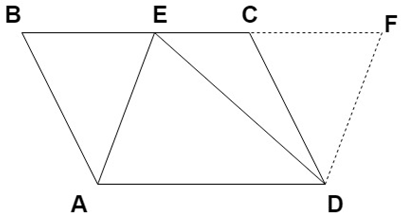
8. From the diagram given below, if area of parallelogram ABCD is ar (ABCD) and area of parallelogram AEFD is ar (AEFD), then what is the relation between ar (ABCD) and ar (AEFD)?

a) ar(ABCD) = ar(AEFD)
b) ar(ABCD) < ar(AEFD)
c) ar(ABCD) > ar(AEFD)
d) There is no relation between areas of the two parallelograms
View Answer

Answer: a
Explanation: According to theorem 9.1, parallelograms on the same base and between the same parallels are equal in area.
As we can see that two parallelograms ABCD and AEFD are on the same base AD and the same parallel line BF, therefore ar (ABCD) = ar (AEFD).

9. From the diagram given below, if area of parallelogram ABCD is ar (ABCD) and area of triangle AED is ar (AED), then what is the relation between ar (ABCD) and ar (AED)?

a) ar (ABCD) = 0.5ar (AED)
b) ar (ABCD) = 4ar (AED)
c) ar (ABCD) = 2ar (AED)
d) ar (ABCD) = ar (AED)
View Answer

Answer: c
Explanation: From theorem 9.1, we know that ar (AEFD) = ar (ABCD) …(1)
Now, ED is the diagonal of the parallelogram AEFD, therefore ar (AED) = \(\frac{1}{2}\) ar (AEFD)
Hence, ar (AED) = \(\frac{1}{2}\) ar (ABCD) …(From (1))

10. From the diagram given below, if area of triangle ABC is ar (ABD) and area of triangle ACD is ar (ACD), then what is the relation between ar (ABD) and ar (ACD)?

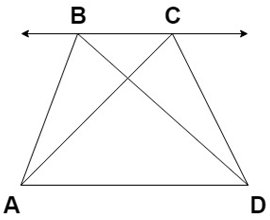
a) ar (ABD) = 0.5ar (ACD)
b) ar (ABC) = 4ar (ACD)
c) ar (ABD) = 2ar (ACD)
d) ar (ABD) = ar (ACD)
View Answer

Answer: d
Explanation: According to theorem 9.2, two triangles on the same base and between the same parallels are equal in area.
As we can see in the diagram that triangle ABD and ACD are on the same base AD and they are on the same line BC which is parallel to base AD, hence ar (ABD) = ar (ACD).

Sanfoundry Global Education & Learning Series – Mathematics – Class 9.

To practice all chapters and topics of class 9 Mathematics, here is complete set of 1000+ Multiple Choice Questions and Answers.

If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]

« Prev - Class 9 Maths MCQ – Areas of Parallelograms and Triangles

» Next - Class 9 Maths MCQ – Parallelograms & Triangles on the Same Base and Between the Same Parallels – 2

Related Posts:

Recommended Articles: