This set of Class 9 Maths Chapter 9 Multiple Choice Questions & Answers (MCQs) focuses on “Parallelograms & Triangles on the Same Base and Between the Same Parallels – 2”.
1. Identify the correct relation if PQRS is a parallelogram.
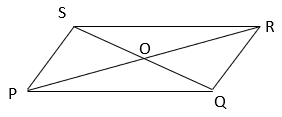
a) ar(POQ) + ar(SOR) > ar(POS) + ar(QOR)
b) ar(POQ) + ar(SOR) = ar(POS) + ar(QOR)
c) ar(POQ) + ar(SOR) < ar(POS) + ar(QOR)
d) ar(POQ) = ar(POS) + ar(SOR)
View Answer
Explanation: Through O, draw AC || PS and BD || PQ
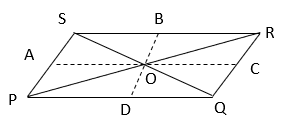
AS POS and PACS are on same base PS and between same parallels PS and AC,
⇒ ar(POS) = ½ ar(PACS) —————(i)
Similarly, ar(QOR) = ½ ar(QACR) ————-(ii)
ar(POQ) = ½ ar(PQBD) ————-(iii)
ar(SOR) = ½ ar(RSBD) ———-(iv)
Adding equation i and ii, ar(POS) + ar(QOR) = ½ ar(PQRS) ——-(v)
Adding equation iii and iv, ar(POQ) + ar(SOR) = ½ ar(PQRS) ——-(vi)
From equation v and vi, ar(POS) + ar(QOR) = ar(POQ) + ar(SOQ).
2. What is the area of triangle ABD if ar(ABC) = 25cm2 and line l || AB?
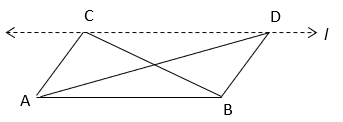
a) 25 cm2
b) 45 cm2
c) 30 cm2
d) 60 cm2
View Answer
Explanation: From figure, ABD and ABC are on same base AB and between same parallels. Since areas of triangles on same base and between same parallels are equal, ar(ABD) = ar(ABC) = 25 cm2.
3. What is the ratio of ar(PQR) / ar(QTS) if T and S are midpoints of QR ad PS respectively?
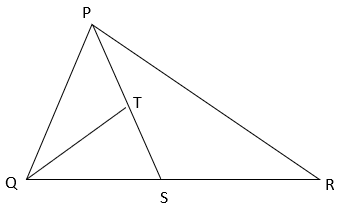
a) 1/2
b) 2
c) 4
d) 1/4
View Answer
Explanation: Since median divides a triangle into 2 triangles of equal area,
ar(ΔPQS) = ½ ar(ΔPQR) ————(i) (PS is median of ΔPQR)
In ΔQPS, TQ is the median
⇒ ar(ΔQTS) = ½ ar(ΔPQS)
⇒ ar(ΔQTS) = ½ x ½ ar(ΔPQR) (from equation i)
⇒ ar(ΔQTS) = ¼ ar(ΔPQR)
⇒ ar(ΔPQS) / ar(ΔQTS) = 4.
4. Which of the following relation is correct if a line through S is drawn parallel to PQ and meets extended QR at A?
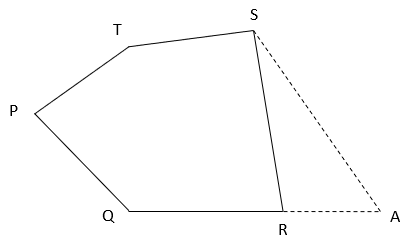
a) ar(PQAT) = ar(PQRST)
b) ar(PQAT) > ar(PQRST)
c) ar(PQAT) < ar(PQRST)
d) ar(PQAT) = ½ ar(PQRST)
View Answer
Explanation: Draw TR || PQ and Join AT
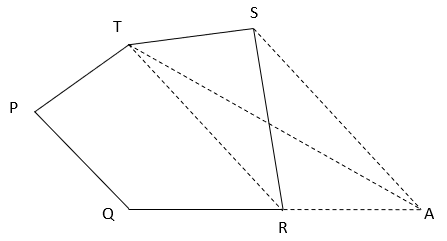
Triangle ATR and STR are on same base RT and between same parallels RT and AS
⇒ ar(ΔATR) = ar(ΔSTR)
⇒ ar(ΔATR) + ar(PQRT) = ar(ΔSTR) + ar(PQRT)
⇒ ar(PQAT) = ar(PQRST).
5. Find the ratio of ar(POQ) / ar(PQR) if O is centroid of triangle PQR.
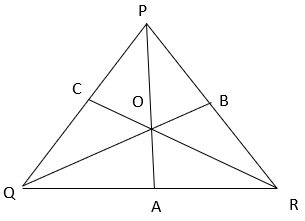
a) 2
b) 1/2
c) 3
d) 1/3
View Answer
Explanation: Centroid is the intersection of medians of a triangle. Hence, PA, QB and RC are the medians.
Since median of triangle divides the triangle into two triangles of equal areas,
ar(PQA) = ar(PRA) = ½ ar(PQR) ———–(i) (AP is median of triangle PQR)
Similarly, ar(QOA) = ar(AOR) = ½ ar(OQR) ———–(ii) (OA is the median of triangle QOR)
Subtracting equation ii from i,
ar(PQA) – ar(QOA) = ar(PRA) – ar(AOR)
⇒ ar(ΔPOQ) = ar(ΔPOR) ————–(iii)
Similarly, ar(QBR) = ar(QBP)and ar(OBR) = ar(OBP)
⇒ ar(QBR) – ar(OBR) = ar(QBP) – ar(OBP)
⇒ ar(ΔPOQ) = ar(ΔQOR) ————–(iv)
From equation iii and iv, ar(ΔPOQ) = ar(ΔQOR) = ar(ΔPOR) ————–(v)
Now, ar(ΔPOQ) + ar(ΔQOR) + ar(ΔPOR) = ar(ΔPQR)
⇒ 3ar(ΔPOQ) = ar(ΔPQR) (from equation v)
⇒ ar(ΔPOQ) = 1/3 ar(ΔPQR).
6. Find the ratio of ar(TRU) / ar(PQRS) if T and U are midpoints and PQRS is a parallelogram.
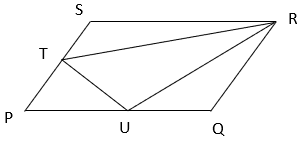
a) 3/8
b) 8/3
c) 3
d) 8
View Answer
Explanation: Join QS
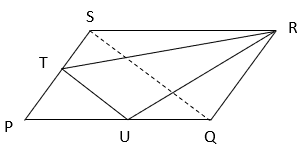
In ΔPQS, TU || QS and T and U are midpoint, TU = ½ QS (by midpoint theorem)
⇒ ar(PTU) = ½ x TU x altitude
⇒ ar(PTU) = ¼ ar(PQS) ( Since TU = ½ QS and altitude of PTU = ½ altitude of PQS)
⇒ ar(PTU) = 1/8 ar(PQRS) —————-(i) (Since ar(PQS) = ½ ar(PQRS))
Since UQR and PQRS are on same base QR and between same parallels QR and PS and UQ = ½ PQ,
ar(UQR) = ¼ ar(PQRS) ———–(ii)
Similarly, STR and PQRS are on same base RS and between same parallels PQ and RS and ST = ½ PS,
ar(STR) = ¼ ar(PQRS) ————-(iii)
Now, ar(ΔTUR) = ar(PQRS) – ar(PTU) – ar(STR) – ar(UQR)
⇒ ar(ΔTUR) = ar(PQRS) – ¼ ar(PQRS) – ¼ ar(PQRS) – ¼ ar(PQRS) [From equation i,ii and iii]
⇒ ar(ΔTUR) = 3/8 ar(PQRS).
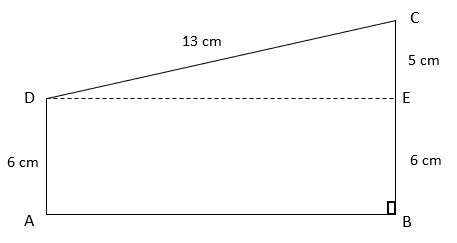
7. What is the area of quadrilateral ABCD?
a) 100 cm2
b) 102 cm2
c) 56 cm2
d) 85 cm2
View Answer
Explanation: From figure, in ΔDEC, ∠DEC = 90°
⇒ DC2 = DE2 + EC2 (By Pythagoras theorem)
⇒ 132 = DE2 + 52
⇒ DE = 12cm
Now, ar(ABCD) = ar(ABED) + ar(DEC)
⇒ ar(ABCD) = (DE x AD) + (1/2 x DE x EC)
⇒ ar(ABCD) = (12 x 6) + (1/2 x 12 x 5)
⇒ ar(ABCD) = 102 cm2.
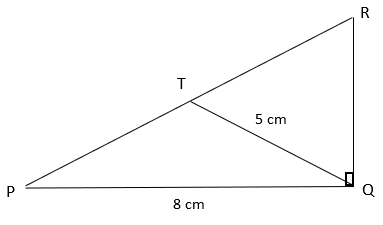
8. Find the area of triangle PQR if PT = PR.
a) 56 cm2
b) 20 cm2
c) 40 cm2
d) 24 cm2
View Answer
Explanation: In right angled triangle, midpoint of hypotenuse is equidistant from the vertices.
⇒ QT = PT = RT = 5 cm
⇒ PR = PT + RT = 10 cm
Now, PT2 = PQ2 + QR2 (By Pythagoras theorem)
⇒ 102 = 82 + QR2
⇒ QR = 6 cm
Now, ar(PQR) = ½ x PQ x QR = ½ x 8 x 6 = 25 cm2.
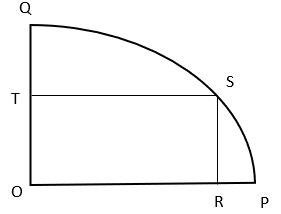
9. If rectangle ORST is inscribed in quadrant of circle of radius 13cm and OT = 5cm, what is the are of quadrilateral ORST?
a) 180 cm2
b) 60 cm2
c) 100 cm2
d) 25 cm2
View Answer
Explanation: From figure, OS = radius of quadrant POQ = 13 cm
and OT = 5 cm
In ΔSOT, OS2 = OT2 + TS2 (By Pythagoras theorem)
⇒ 132 = 52 + TS2
⇒ TS = 12 cm
Now, ar(ORST) = OT x TS = 12 x 5 = 60 cm2.
10. Find the area of quadrilateral PQRS.
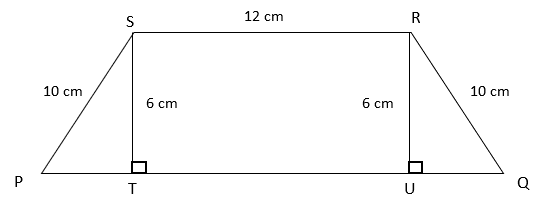
a) 120 cm2
b) 76 cm2
c) 60 cm2
d) 150 cm2
View Answer
Explanation: From figure, in ΔPTS, PS2 = PT2 + TS2 (By Pythagoras theorem)
⇒ 102 = PT2 + 62
⇒ PT = 8 cm
Similarly, UQ = 8cm
Since UTRS is rectangle, RS = UT = 12 cm
⇒ PQ = PT + UT + UQ = 28 cm
Now, ar(trapezium PQRS) = ½ x sum of parallel sides x altitude
⇒ ar(PQRS) = ½ x (28 + 12) x 6 = 120 cm2.
Sanfoundry Global Education & Learning Series – Mathematics – Class 9.
To practice all chapters and topics of class 9 Mathematics, here is complete set of 1000+ Multiple Choice Questions and Answers.
- Check Class 9 - Mathematics Books
- Practice Class 10 Mathematics MCQs
- Practice Class 8 Mathematics MCQs
