This set of Mathematics Multiple Choice Questions & Answers (MCQs) focuses on “Angle Sum Property of a Triangle”.
1. Find the value of x.
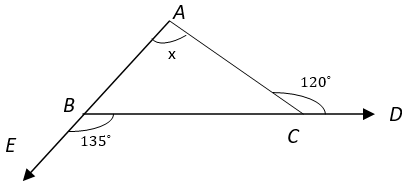
a) 90°
b) 75°
c) 135°
d) 45°
View Answer
Explanation: From figure, ∠EBC + ∠ABC = 180° (Linear Pair)
⇒ 135° + ∠ABC = 180°
⇒ ∠ABC = 45°
Also, ∠ACB + ∠ACD = 180° (Linear Pair)
⇒ 120° + ∠ACB = 180°
⇒ ∠ACB = 60°
In ∆ ABC, ∠BAC + ∠ABC + ∠ACB = 180° (Angle Sum property of triangle)
⇒ 45° + x + 60° = 180°
⇒ x = 180° – 105°
⇒ x = 75°
2. Which of the following relation between x and y is correct?
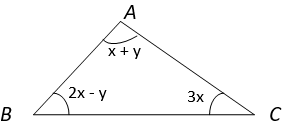
a) x + y = 45°
b) x – y = 180°
c) 3x + y = 90°
d) 3x – y = 90°
View Answer
Explanation: In ∆ ABC, ∠BAC + ∠ABC + ∠ACB = 180° (Angle Sum property of triangle)
⇒ (x + y) + (2x – y) + (3x) = 180°
⇒ 6x – 2y = 180°
⇒ 3x – y = 90°
3. Find the angles (∠P, ∠Q, ∠R) of the triangle if a + b = 120° and a – c = 30°.
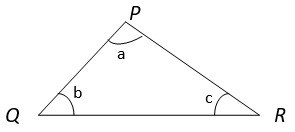
a) 90°, 30°, 60°
b) 90°, 45°, 45°
c) 120°, 30°, 30°
d) 90°, 45°, 80°
View Answer
Explanation: Given, a + b = 120° ———— (i)
and a – c = 30°———— (ii)
In ∆ PQR, ∠P + ∠Q + ∠R = 180° (Angle Sum property of triangle)
⇒ a + b + c = 180°
⇒ 120° + c = 180° (from equation i)
⇒ c = 60°
Now, from equation ii, a – c = 30°
⇒ a – 60° = 30°
⇒ a = 90°
Also, from equation i, a + b = 120°
⇒ b + 90° = 120°
⇒ b = 30°
4. Find the angle ∠MQR if QM ⊥ PR and ∠Q = 90°.
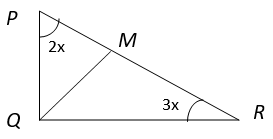
a) 60°
b) 45°
c) 36°
d) 90°
View Answer
Explanation: In ∆ PQR, ∠P + ∠Q + ∠R = 180° (Angle Sum property of triangle)
⇒ 2x + 90° + 3x = 180°
⇒ 5x = 90°
⇒ x = 18°
Now, In ∆ QMR, ∠MQR + ∠QMR + ∠MRQ = 180° (Angle Sum property of triangle)
⇒ ∠MQR + 90° + 3x = 180°
⇒ ∠MQR = 180° – 90° – 3 x 18°
⇒ ∠MQR = 180° – 90° – 54°
⇒ ∠MQR = 36°
5. Find the value of x if BO and OC are angle bisectors of angle B and C respectively.
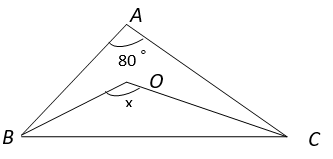
a) 90°
b) 130°
c) 145°
d) 55°
View Answer
Explanation: In ∆ ABC, ∠BAC + ∠ABC + ∠ACB = 180° (Angle Sum property of triangle)
⇒ 80° + ∠B + ∠C = 180°
⇒ ∠B + ∠C = 100° ————- (i)
Also, In ∆ BOC, ∠BOC + ∠OBC + ∠OCB = 180° (Angle Sum property of triangle)
⇒ ∠BOC + 1/2 ∠B + 1/2 ∠C = 180° (BO and OC are angle bisectors)
⇒ ∠BOC + 1/2 (∠B + ∠C) = 180°
⇒ ∠BOC + 1/2 (100°) = 180° (from equation i)
⇒ ∠BOC = 180° – 50°
⇒ ∠BOC = 130°.
6. Find the angle ∠SOR if PQ || RS and ∠OSR : ∠SRO = 2 : 3.
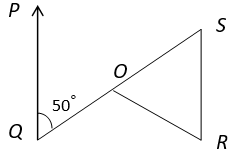
a) 160°
b) 85°
c) 35°
d) 55°
View Answer
Explanation: PQ || RS ⇒ ∠QPS = ∠PSR = 50° (Alternate Interior Angles)
In ∆ SOR, ∠OSR : ∠SRO = 2 : 3
⇒ ∠SRO = 3/2 x ∠OSR
⇒ ∠SRO = 3/2 x 100°
⇒ ∠SRO = 75°
Also, ∠OSR + ∠SRO + ∠ROS = 180° (Angle Sum property of triangle)
⇒ 50° + 75° + ∠ROS = 180°
⇒ ∠ROS = 180° – 125°
⇒ ∠ROS = 55°.
7. Find the angle ∠BCD if AD || BC and x = 2y/3 and y = 3z/5.
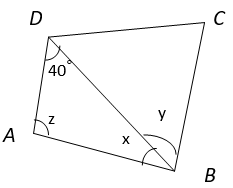
a) 80°
b) 75°
c) 55°
d) 32°
View Answer
Explanation: x = 2y/3 and y = 3z/5
In ∆ ADB, x + y + 40° = 180° (Angle Sum property of triangle)
⇒ 2/3y + z = 140°
⇒ 2/3 x (3z/5) + z = 140°
⇒ (6z/15) + z = 140°
⇒ 21z/15 = 140°
⇒ z = 100°
Now, y = 3z/5 = 60°
and x = 2y/3 = 40°
Also, AD || BC ⇒ ∠CDB = ∠DBA = 40° (Alternate Interior Angles)
In ∆ CDB, ∠CDB + ∠CBD + ∠BCD = 180° (Angle Sum property of triangle)
⇒ 60° + 40° + ∠BCD = 180°
⇒ ∠BCD = 180° – 100°
⇒ ∠BCD = 80°.
8. Find x if PQ || RS and ∠1 : ∠2 = 3 : 5.
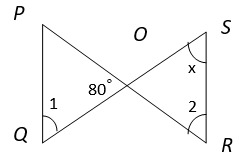
a) 60°
b) 75°
c) 37.5°
d) 135°
View Answer
Explanation: PQ || RS ⇒ ∠PQO = ∠OSR (Alternate Interior Angles)
⇒ ∠1 = x ——— (i)
Also, ∠POQ = ∠SOR (Vertically Opposite Angles)
⇒ ∠SOR = 80°
In ∆ SOR, ∠OSR + ∠SRO + ∠ROS = 180° (Angle Sum property of triangle)
⇒ x + ∠2 + 80° = 180°
⇒ ∠1 + ∠2 = 100°
⇒ ∠1 + (5/3) ∠1 = 100° (∠1 : ∠2 = 3 : 5)
⇒ (8/3) ∠1 = 100°
⇒ ∠1 = 37.5°
From equation (i), x = ∠1 = 37.5°.
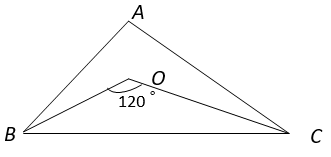
9. Find the type of the ∆ ABC if angle B and C are equal.
a) Right angled triangle
b) Equilateral triangle
c) Obtuse angled triangle
d) Scalene triangle
View Answer
Explanation: In ∆ ABC, ∠BAC + ∠ABC + ∠ACB = 180° (Angle Sum property of triangle)
⇒ ∠A + 2∠B = 180° ————- (i) (Since ∠B = ∠C)
Also, In ∆ BOC, ∠BOC + ∠OBC + ∠OCB = 180° (Angle Sum property of triangle)
⇒ ∠BOC + 1/2 ∠B + 1/2 ∠C = 180° (BO and OC are angle bisectors)
⇒ 120° + 1/2 (∠B + ∠B) = 180° (Since ∠B = ∠C)
⇒ 1/2 (2∠B) = 60°
⇒ ∠B = 60°
⇒ ∠C = 60°
From equation (i), ∠A + 2 x 60° = 180°
⇒ ∠A = 60°
∠A = ∠B = ∠C = 60° ⇒ ∆ ABC is an equilateral triangle.
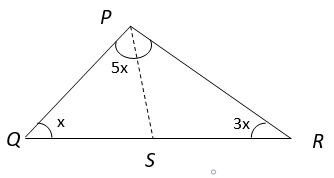
10. Find the angles ∠PSR and ∠PSQ if PS is angle bisector of ∠P and the angles of ∆ ABC are in the ratio 1 : 3 : 5.
a) 90°, 90°
b) 110°, 70°
c) 30°, 60°
d) 120°, 30°
View Answer
Explanation: In ∆ PQR, ∠P + ∠Q + ∠R = 180° (Angle Sum property of triangle)
⇒ x + 3x + 5x = 180°
⇒ 9x = 180°
⇒ x = 20°
Now, In ∆ QSP, ∠QPS = 100°/2 = 50° (PS is angle bisector of ∠P)
∠QPS + ∠PQS + ∠PSQ = 180° (Angle Sum property of triangle)
⇒ 50°+ 20°+ ∠PSQ = 180°
⇒ ∠PSQ = 110°
Now, ∠PSQ + ∠PSR = 180° (Linear Pair)
⇒ 110° + ∠PSR = 180°
⇒ ∠PSR = 70°.
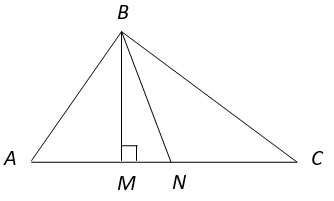
11. Which among the following relation is correct if BM ⊥ AC and BN is angle bisector of ∠ABC?
a) ∠MBN = 1/2 (∠A – ∠C)
b) ∠MBN = 1/2 (∠A + ∠C)
c) ∠MBN = (∠A – ∠C)
d) ∠MBN = (∠A + ∠C)
View Answer
Explanation: In ∆ ABM, ∠BAM + ∠ABM + ∠BMA = 180° (Angle Sum property of triangle)
⇒ ∠BAM + ∠ABM + 90° = 180°
⇒ ∠BAM = 90° – ∠ABM ———(i)
In ∆ MBC, ∠BMC + ∠MBC + ∠BCM = 180° (Angle Sum property of triangle)
⇒ ∠MBC + ∠BCM + 90° = 180°
⇒ ∠BCM = 90° – ∠MBC ———(ii)
Subtracting equation (i) and (ii),
∠BAM – ∠BCM = 90° – ∠ABM – (90° – ∠MBC)
⇒ ∠A – ∠C = 90° – ∠ABM – 90° + ∠MBC
⇒ ∠A – ∠C = ∠MBC – ∠ABM
⇒ ∠A – ∠C = ∠MBN + ∠NBC – (∠ABN – ∠MBN)
⇒ ∠A – ∠C = ∠MBN + ∠NBC – ∠ABN + ∠MBN
⇒ ∠A – ∠C = 2 ∠MBN (Since ∠NBC = ∠ABN, BN is angle bisector of ∠B)
⇒ ∠MBN = 1/2 (∠A – ∠C)
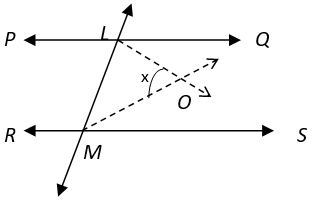
12. Find x if PQ || RS and MO and LO are angle bisectors.
a) 60°
b) 75°
c) 90°
d) 45°
View Answer
Explanation:
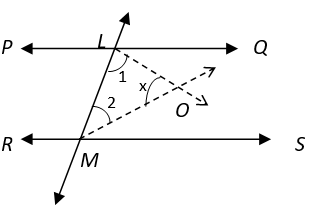
∠QLM = 2 ∠OLM and ∠SML = 2 ∠OML (MO and LO are angle bisectors)
PQ || RS ⇒ ∠QLM + ∠SML = 180° (Interior Angles on the same side of transversal)
⇒ 1/2 (∠OLM) + 1/2 (∠OML) = 180°
⇒ 1/2 (∠1) + 1/2 (∠2) = 180°
⇒ ∠1 + ∠2 = 90° ——— (i)
In ∆ LOM, ∠OLM + ∠MOL + ∠OML = 180° (Angle Sum property of triangle)
⇒ ∠1 + ∠2 + ∠MOL = 180°
⇒ 90° + ∠MOL = 100° (From equation i)
⇒ ∠MOL = 90°.
13. Which among the following relation is correct if PO and RO are angle bisectors?
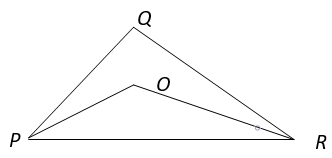
a) ∠POR = 90°
b) ∠POR = 90° – ∠Q
c) ∠POR = 90° – ∠Q/2
d) ∠POR = 90° + ∠Q/2
View Answer
Explanation: As PO and RO are angle bisectors, ∠P = 2∠OPR ————(i)
and ∠R = 2∠ORP ————- (ii)
In ∆ PQR, ∠P + ∠Q + ∠R = 180° ———- (iii) (Angle Sum property of triangle)
In ∆ POR, ∠OPR + ∠POR + ∠ORP = 180° (Angle Sum property of triangle)
⇒ 1/2 ∠P + ∠POR + 1/2 ∠R = 180° (From equation i and ii)
⇒ 1/2 (∠P + ∠R) + ∠POR = 180°
⇒ 1/2 (180° – ∠Q) + ∠POR = 180° (From equation iii)
⇒ 90° – 1/2 ∠Q + ∠POR = 180°
⇒ ∠POR = 180° – 90° + 1/2 ∠Q
⇒ ∠POR = 90° + \(\frac{1}{2}\)(∠Q).
14. The sum of the angles of a triangle is equal to __________
a) 270°
b) 90°
c) 180°
d) 360°
View Answer
Explanation: According to theorem 6.7, the sum of the angles of a triangle is equal to 180°.
As shown in the diagram below, three angles of the triangles are ∠1, ∠2 and ∠3.
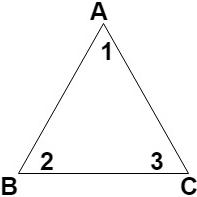
Hence, ∠1 + ∠2 + ∠3 = 180°
15. From the diagram given below, what is the value of ∠CBA?
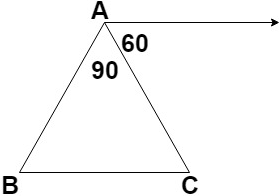
a) 30°
b) 60°
c) 90°
d) 100°
View Answer
Explanation: As can be seen from the diagram that ∠OAC and ∠ACB are pair of alternate interior angles.
Hence, ∠OAC = ∠ACB
∠ACB = 60°
Now it is given that ∠BAC = 90° and we know that
∠BAC + ∠ACB + ∠CBA = 180° (Theorem 6.7)
90° + 60° + ∠CBA = 180°
∠CBA = 180° – 90° – 60°
∠CBA = 30°
16. From the diagram given below, what is the value of ∠ACB?
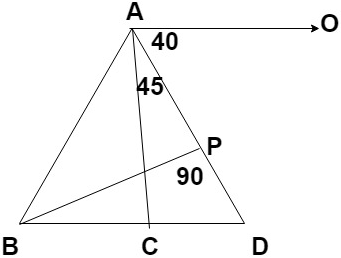
a) 45°
b) 40°
c) 140°
d) 85°
View Answer
Explanation: It can be seen in the diagram that ∠OAD and ∠ADC are pair of exterior angles, hence ∠OAD = ∠ADC
Therefore, ∠ADC = 40°
Now according to theorem 6.8, if a side of a triangle is produced, then the exterior angle so formed is equal to the sum of two interior opposite angles.
It means that ∠ACB = ∠CAD + ∠CDA
Hence, ∠ACB = 45° + 40°
∠ACB = 85°
Sanfoundry Global Education & Learning Series – Mathematics – Class 9.
To practice all areas of Mathematics, here is complete set of 1000+ Multiple Choice Questions and Answers.
- Practice Class 10 Mathematics MCQs
- Buy Class 9 - Mathematics Books
- Practice Class 8 Mathematics MCQs
