This set of Class 9 Maths Chapter 6 Multiple Choice Questions & Answers (MCQs) focuses on “Linear Pair of Angles”.
1. Identify the linear pair of angles from the given options.
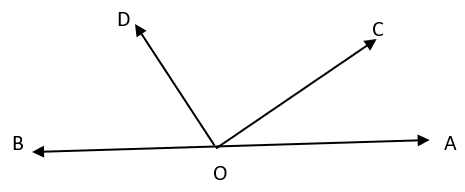
a) ∠AOB and ∠AOC
b) ∠AOC and ∠COD
c) ∠AOC and ∠COB
d) ∠AOD and ∠DOC
View Answer
Explanation: Two adjacent angles form a linear pair of angles if their non-common arms are two opposite rays. In the given figure, there are two linear pairs: (i) ∠AOC and ∠COB and (ii) ∠AOD and ∠DOB.
2. Which of the following options are satisfy the condition that POQ is a line?
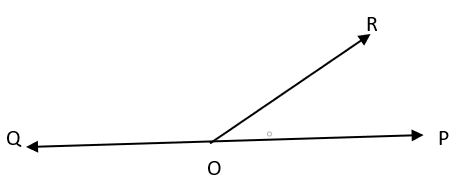
a) ∠POQ + ∠POR = 180°
b) ∠POR + ∠ROQ = 360°
c) ∠POR – ∠ROQ = 180°
d) ∠POR + ∠ROQ = 180°
View Answer
Explanation: If the sum of two adjacent angles are 180°, then their non-common arms are two opposite rays and form a linear pair of angles. In the given figure, ∠POR and ∠ROQ form a linear pair and ∠POR + ∠ROQ = 180°.
3. Find the value of k if ∠POQ and ∠POR form a linear pair.
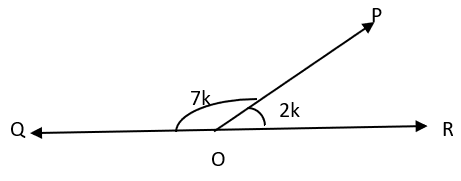
a) 20°
b) 120°
c) 40°
d) 50°
View Answer
Explanation: Since ∠POQ and ∠POR form a linear pair of angles, ∠POQ + ∠POR = 180°.
From the figure, ∠POQ = 7k, ∠POR = 2k
∠POQ + ∠POR = 180°
⇒ 7k + 2k = 180°
⇒ 9k = 180°
⇒ k = 20°
4. Find the value of ∠BOD if ∠AOD : ∠AOC = 4 : 5.
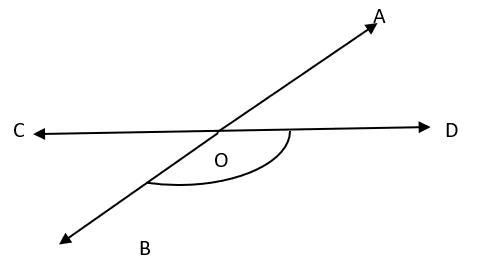
a) 20°
b) 100°
c) 140°
d) 50°
View Answer
Explanation: ∠AOC and ∠AOD form a linear pair of angles, ∠AOC + ∠AOD = 180°.
Also, ∠AOD: ∠AOC = 4:5
∠AOC + ∠AOD = 180°
⇒ ∠AOC + (4/5) ∠AOC = 180
⇒ 9∠AOC = 180 * 5
⇒ ∠AOC = 100°
Now, ∠BOD = ∠AOC (Vertically opposite angles)
⇒ ∠BOD = 100°.
5. What is the value of x in the given figure?
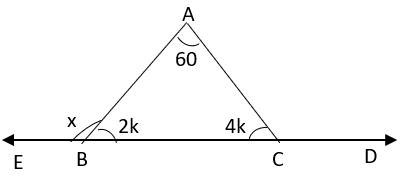
a) 120°
b) 100°
c) 40°
d) 140°
View Answer
Explanation: In triangle ABC, ∠A + ∠B + ∠C = 180°
⇒ 60° + 2k + 4k = 180°
⇒ 6k = 120°
⇒ k = 20°
Now, x + ∠ABC = 180°
⇒ x + 2k = 180°
⇒ x = 180° – 2 * 20°
⇒ x = 140°
6. Find the value of y if OF is the angle bisector of ∠COB.
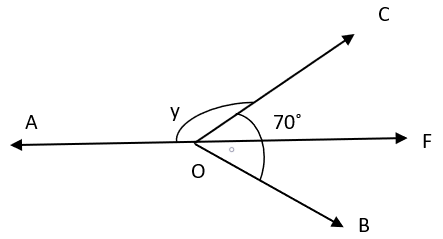
a) 145°
b) 100°
c) 40°
d) 80°
View Answer
Explanation: Since, OF is the angle bisector of ∠COB, ∠COF = ∠BOF = 70°/2 = 35°.
∠AOC + ∠COF = 180° (Linear Pair)
⇒ y + 35° = 180°
⇒ y = 145°
7. What is the value of ∠COF?
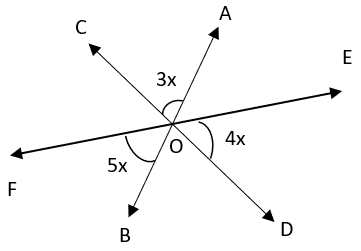
a) 45°
b) 150°
c) 60°
d) 180°
View Answer
Explanation:
∠AOC = ∠BOD = 3x (Vertically Opposite Angles)
∠COF = ∠EOD = 4x (Vertically Opposite Angles)
∠BOF = ∠AOE = 5x (Vertically Opposite Angles)
Now, sum of all angles around a point is 360°
⇒ ∠BOF + ∠AOE + ∠COF + ∠EOD + ∠AOC + ∠BOD = 360°
⇒ 5x + 5x + 4x + 4x + 3x + 3x = 360°
⇒ 24x = 360°
⇒ x = 15°
∠COF = 4x = 4 x 15 = 60°
8. What is the value of k if ∠BOD and ∠COE are right angles?
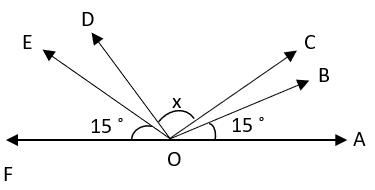
a) 30°
b) 150°
c) 60°
d) 120°
View Answer
Explanation: ∠BOD = ∠COE = 90°
∠BOC = 90 – k
∠EOD = 90 – k
∠BOF + ∠BOA = 180° (Linear Pair)
⇒ (90 – k) + k + 15 + (90 – k) + 15 = 180°
⇒ k = 30°
9. Find the value of x and y if x – y = 30°.
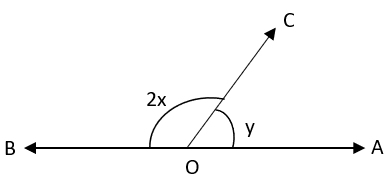
a) 35°, 35°
b) 50°, 40°
c) 60°, 30°
d) 20°, 35°
View Answer
Explanation: ∠AOC + ∠BOC = 180° (Linear Pair)
⇒ 2x + y = 180° —– (1)
Also, x – y = 30° —- (2)
Adding equation (1) and (2), we get x = 60°
Substituting the value of x in equation (1), y = 30°.
10. Find the value of x.
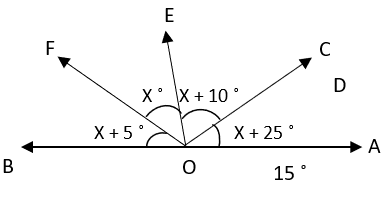
a) 45°
b) 40°
c) 60°
d) 35°
View Answer
Explanation: ∠AOC + ∠BOC = 180° (Linear Pair)
∠AOC = (x + 5) + x
∠BOC = (x + 10) + (x + 25)
⇒ ∠AOC + ∠BOC = 180°
⇒ (x + 5) + x + (x + 10) + (x + 25) = 180°
⇒ 4x + 40 = 180°
⇒ x = 140°/4
⇒ x = 35°
Sanfoundry Global Education & Learning Series – Mathematics – Class 9.
To practice all chapters and topics of class 9 Mathematics, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
- Practice Class 10 Mathematics MCQs
- Practice Class 8 Mathematics MCQs
- Check Class 9 - Mathematics Books
