This set of Class 9 Maths Chapter 6 Multiple Choice Questions & Answers (MCQs) focuses on “Parallel Lines and Transversal – 1”.
1. From the given diagram, which is the transversal?
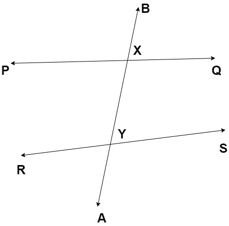
a) Line PQ
b) Line AB
c) Line RS
d) Line PS
View Answer
Explanation: A line which intersects two or more lines at distinct points is called transversal. It can be seen in the given diagram that line AB intersects line PQ and RS at points X and Y respectively. Hence, line AB is transversal.
2. From the given diagram, which is the pair of corresponding angles?
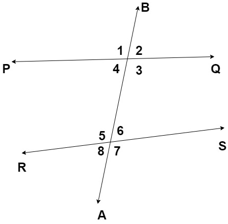
a) ∠1 and ∠5
b) ∠1 and ∠2
c) ∠1 and ∠3
d) ∠1 and ∠7
View Answer
Explanation: In the given diagram, ∠1 and ∠5 is the pair of corresponding angles. Similarly, other pairs of corresponding angles are ∠2 and ∠6, ∠4 and ∠8, ∠3 and ∠7.
Note: To easily remember the corresponding angles, observe that all the pairs are of “F shape.”
3. From the given diagram, which is the pair of alternate interior angles?
a) ∠4 and ∠8
b) ∠1 and ∠7
c) ∠4 and ∠6
d) ∠4 and ∠5
View Answer
Explanation: In the given diagram, ∠4 and ∠6 is the pair of corresponding angles. Similarly, other pairs of corresponding angles are ∠3 and ∠5.
Note: To easily remember the alternate interior angles, observe that all the pairs are of “Z or S shape.”
4. From the diagram given below, if lines PQ and RS are parallel, then what is the relation between corresponding angles ∠1 and ∠5?
a) ∠1 > ∠5
b) ∠1 < ∠5
c) ∠1 >>> ∠5
d) ∠1 = ∠5
View Answer
Explanation: According to axiom 6.3, if a transversal intersects two parallel lines, then each pair of corresponding angles is equal. The reverse of this statement is also true.
Hence, ∠1 = ∠5 and likewise for other corresponding angles, ∠2 = ∠6, ∠4 = ∠8, ∠3 = ∠7.
5. From the diagram given below, if lines PQ and RS are parallel, then what is the relation between alternate interior angles ∠4 and ∠6?
a) ∠4 > ∠6
b) ∠4 < ∠6
c) ∠4 >>> ∠6
d) ∠4 = ∠6
View Answer
Explanation: According to theorem 6.2, if a transversal intersects two parallel lines, then each pair of interior angles is equal. The reverse of this statement is also true.
Hence, ∠4 = ∠6 and likewise for other corresponding angles, ∠3 = ∠5.
6. From the given diagram, if a transversal intersects two parallel lines, then what is the relation between pair of alternate interior angles ∠4 and ∠5?
a) ∠4 + ∠5 = 180°
b) ∠4 + ∠5 = 90°
c) ∠4 = ∠5
d) ∠4 > ∠5
View Answer
Explanation: According to theorem 6.4, if a transversal intersects two parallel lines, then each pair of interior angles on the same side is supplementary. i.e. sum of those two angles is equal to 180°.
Hence, ∠4 + ∠5 = 180°.
7. As shown in below diagram, if two lines l and m are parallel to third line p, then lines l and m are __________
a) perpendicular
b) parallel
c) intersecting
d) non intersecting
View Answer
Explanation: According to theorem 6.6, lines which are parallel to the same line are parallel to each other.
Since the lines l and m are parallel to the same line p, we can say that lines l and m are parallel to each other.
8. From the given diagram below, if ∠BOQ = 120°, then what are the values of angles x and y?
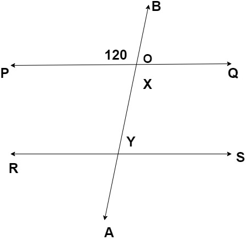
a) 120° & 120°
b) 75° & 45°
c) 120° & 60°
d) 120° & 45°
View Answer
Explanation: Since ∠BOP & ∠x are pair of vertically opposite angles,
∠x = ∠BOP
Hence, ∠x = 120°.
Now, according to theorem 6.4, angle x and angle y are supplementary.
Therefore, ∠x + ∠y = 180°
∠y = 180° – ∠x
= 180° – 120°
= 60°.
Sanfoundry Global Education & Learning Series – Mathematics – Class 9.
To practice all chapters and topics of class 9 Mathematics, here is complete set of 1000+ Multiple Choice Questions and Answers.
- Practice Class 10 Mathematics MCQs
- Check Class 9 - Mathematics Books
- Practice Class 8 Mathematics MCQs
