This set of Class 9 Maths Chapter 5 Multiple Choice Questions & Answers (MCQs) focuses on “Equivalent Versions of Euclid’s Fifth Postulate”.
1. When the sum of the measures of the interior angles on the same side of the falling line is greater than 180 degree, then the two straight lines, if produced indefinitely, meet on that side on which the sum of angles is greater than 180 degree.
a) True
b) False
View Answer
Explanation: The given statement is slightly different from Euclid’s 5th postulate which is “When the sum of the measures of the interior angles on the same side of the falling line is less than two right angles (<180), then the two straight lines, if produced indefinitely, meet on that side on which the sum of angles is less than two right angles.”
It can be understood by the diagram given below.
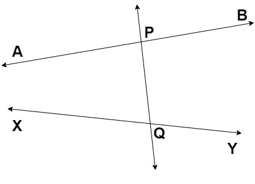
Falling line is PQ and sum of two angles BPQ and YQP is greater than 180 degree and we can see that lines AB and XY will not meet on the right side of the line PQ.
2. “For every line x and for every point o not lying on x, there exists a unique line y passing through o and parallel to x.” This statement is __________
a) Pythagoras’ theorem
b) Heron’s theorem
c) Thales’ theorem
d) Playfair’s axiom
View Answer
Explanation: The given statement is Playfair’s axiom which is in fact, equivalent version of Euclid’s fifth postulate.
It can be understood by seeing the diagram given below.
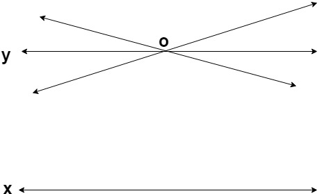
We can see that lines x and y are parallel, i.e. they will not intersect each other.
Sanfoundry Global Education & Learning Series – Mathematics – Class 9.
To practice all chapters and topics of class 9 Mathematics, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
- Check Class 9 - Mathematics Books
- Practice Class 8 Mathematics MCQs
- Practice Class 10 Mathematics MCQs
