This set of Class 9 Maths Chapter 8 Multiple Choice Questions & Answers (MCQs) focuses on “Quadrilaterals – Properties of a Parallelogram – 2”.
1. Which of the following is not a parallelogram?
a)
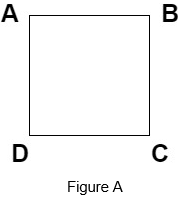
b)
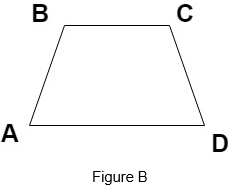
c)
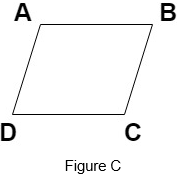
d)
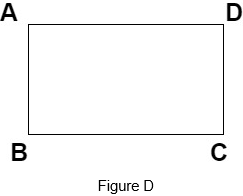
View Answer
Explanation: A quadrilateral is said to be a parallelogram if each pair of opposite sides is parallel but as we can see in the Figure B, trapezium has only one pair of sides which are parallel hence, it is not parallelogram.
2. As shown in the diagram below, for the same perimeter, areas of rectangle and parallelogram are same.
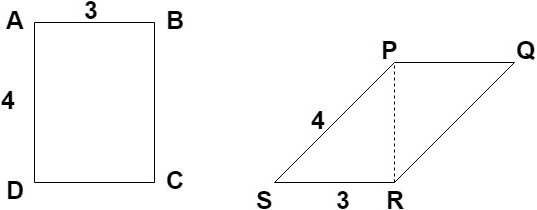
a) True
b) False
View Answer
Explanation: For rectangle, area = AD * AB and
for parallelogram, area = PR * SR
We can see that AB = SR = 3 but PR < AD hence area of parallelogram < area of rectangle.
3. From the given diagram, what can be said about ∆ADB and ∆BCD?
a) They are congruent to each other
b) They are not congruent to each other
c) ∠ABD = ∠ADB
d) ∠BDC = ∠DBC
View Answer
Explanation: We can see that diagonal BD divides the parallelogram into two triangles ABD and BDC.
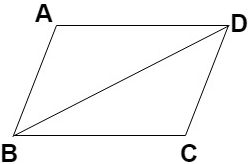
Now, for these two triangles,
∠ADB = ∠DBC (Pair of alternate angles)
BD = BD (Same sides)
∠ABD = ∠BDC (Pair of alternate angles)
Therefore, according to ASA rule, we can say that triangles ABD and BDC are congruent to each other.
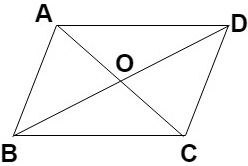
4. From the diagram, if BD and AC are diagonals of a parallelogram ABCD then what is true for them?
a) BO = AO
b) BO = OC
c) BO = OD
d) AO = OD
View Answer
Explanation: According to theorem 8.6, diagonal of a parallelogram bisect each other.
It means that BO = OD and AO = OC.
5. Which of the following relation is correct if ABCD is a parallelogram and BF and DE are perpendiculars to AC?
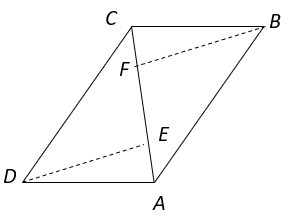
a) DE = BF
b) DE < BF
c) DE > BF
d) DE = 2BF
View Answer
Explanation: In ΔADE and ΔBFC,
∠DAC = ∠BCA (Alternate interior angles)
∠DEA = ∠BFA (Right angles)
AD = BC (Opposite sides of parallelogram)
⇒ ΔADE ≅ ΔBFC (AAS congruence criteria)
⇒ DE = BF (Corresponding parts of congruent triangles).
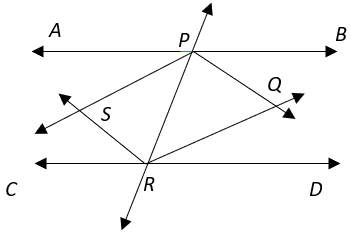
6. Identify the quadrilateral formed by the angle bisectors of the interior angles formed between two parallel lines.
a) Square
b) Circle
c) Rhombus
d) Rectangle
View Answer
Explanation: Since AB || CD,
∠APR = ∠DRP (Alternate interior angles)
⇒ ½ ∠APR = ½ ∠DRP
⇒ ∠SPR = ∠QRP
⇒ PS || RQ ———– (i)
Similarly, ∠BPR = ∠CRP (Alternate interior angles)
⇒ ½ ∠BPR = ½ ∠CRP
⇒ ∠QPR = ∠SRP
⇒ PQ || RS ———– (ii)
Also, ∠APR + ∠RPB = 180° (Linear Pair)
⇒ ½ ∠APR + ½ ∠RPB = ½ x 180°
⇒ ∠SPR + ∠RPQ = 90°
⇒ ∠SPQ = 90°
Hence, PQRS is a rectangle.
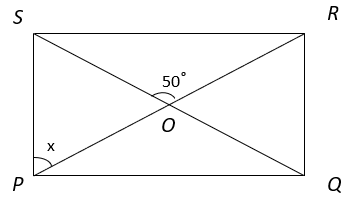
7. Find the value of x in the rectangle PQRS.
a) 36°
b) 25°
c) 97°
d) 128°
View Answer
Explanation: From figure, ∠POQ = 50° ———- (i) (Vertically opposite angles)
Diagonals of rectangle are equal and bisect each other
⇒ OP = OQ ————–(ii)
In ΔPOQ, OP = OQ
⇒ ∠OPQ = ∠OQP ———- (iii) (Angles opposite to equal sides are equal)
Also, ∠QPO + ∠OQP + ∠POQ = 180° (Angle sum property of triangle)
⇒ 2∠OPQ + 50° = 180° (from equation i and iii)
⇒ ∠OPQ = 65° —————- (iv)
Also, ∠SPQ = 90° (Angle of rectangle)
⇒ ∠SPO + ∠OPQ = 90°
⇒ x + 65° = 90° (from equation iv)
⇒ x = 25°.
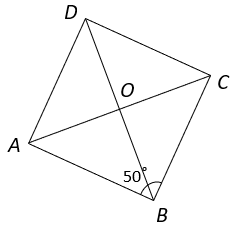
8. If ABCD is a rhombus, then what is the value of ∠OAD?
a) 75°
b) 27°
c) 65°
d) 82°
View Answer
Explanation: From figure, ABCD is a parallelogram
and ∠ABC = ∠ADC = 50° ———- (i) (Opposite angles of a parallelogram)
⇒ ½ ∠ADC = ½ x 50° (Diagonals of parallelogram are angle bisectors)
⇒ ∠ADO = 25° ———— (ii)
In ΔAOD, ∠AOD = 90° ———–(iii) (Diagonals of rhombus are perpendicular to each other)
Also, ∠AOD + ∠OAD + ∠ADO = 180° (Angle sum property of triangle)
⇒ 90° + ∠OAD + 25° = 180° (from equation ii and iii)
⇒ ∠OAD = 65°.
Sanfoundry Global Education & Learning Series – Mathematics – Class 9.
To practice all chapters and topics of class 9 Mathematics, here is complete set of 1000+ Multiple Choice Questions and Answers.
- Practice Class 8 Mathematics MCQs
- Practice Class 10 Mathematics MCQs
- Check Class 9 - Mathematics Books
