This set of Mathematics Multiple Choice Questions & Answers (MCQs) focuses on “Properties of a Parallelogram – 1”.
1. What is the quadrilateral formed by the angle bisectors of a parallelogram?
a) Square
b) Rectangle
c) Circle
d) Rhombus
View Answer
Explanation:
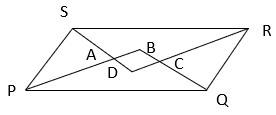
PQ || RS ⇒ ∠P + ∠S = 180° (Interior angles on the same side of transversal)
⇒ ½ ∠P + ½ ∠S = ½ x 180°
⇒ ∠APS + ∠PSA = 90° ——————-(i)
In ΔASP, ∠APS + ∠PSA + ∠SAP = 180° (Angle sum property of triangle)
⇒ 90° + ∠SAP = 180° (from equation i)
⇒ ∠SAP = 90°
⇒ ∠DAB = 90° (Vertically opposite angle)
Similarly, ∠ADB = 90°, ∠ABC = 90°, ∠DCB = 90°.
Hence, ABCD is a rectangle.
2. Find the value of x if PQRS is a parallelogram.
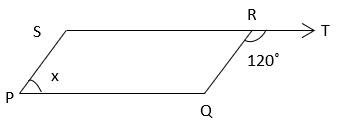
a) 150°
b) 50°
c) 60°
d) 120°
View Answer
Explanation: ∠SRQ + ∠QRT = 180° (Linear Pair)
⇒ ∠SRQ = 60°
In parallelogram PQRS, ∠SRQ = ∠QPS (Opposite angles of a parallelogram are equal)
⇒ x = 60°.
3. What are the values of x and y if ABCD is a parallelogram?
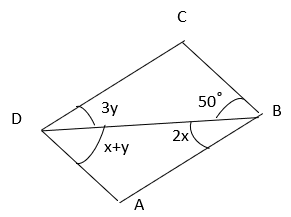
a) 30°, 20°
b) 130°, 120°
c) 150°, 160°
d) 10°, 40°
View Answer
Explanation: Since ABCD is a parallelogram, AB || CD
⇒ ∠CDB = ∠ABD and ∠CBD = ∠ADB (Alternate interior angles)
Hence, 3y = 2x ————(i)
And x + y = 50° ——————- (ii)
Solving equation i and ii, x = 30°, y = 20°.
4. Given PQRS is a parallelogram, what is the ratio of OQ/OR if PR = 10cm and QS = 12cm?
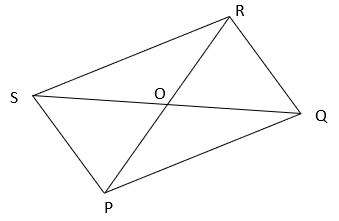
a) 1.2
b) 1.5
c) 1.8
d) 2
View Answer
Explanation: Since Diagonals of parallelogram bisect each other
⇒ OQ = QS/2 = 6cm
And OR = PR/2 = 5cm
⇒ OQ/OR = 6/5 = 1.2.
5. Which of the following relation is correct if ABCD and CDEA are parallelogram?
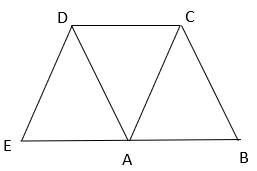
a) CD = EB
b) CD = EB/2
c) CD = 2EB
d) CD = EB/4
View Answer
Explanation: Since ABCD is a parallelogram,
AB = CD ———-(i) (Opposite sides of parallelogram are equal)
Since CDEA is a parallelogram,
EA = CD ———-(ii) (Opposite sides of parallelogram are equal)
Adding equation i and ii,
AB + EA = 2CD
⇒ EB = 2CD
⇒ CD = EB/2.
6. PQRS is a parallelogram and U and T are midpoints of side RS and PQ respectively. Identify the correct relation from the given options.
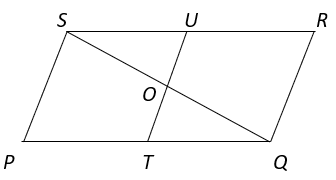
a) OU > OT
b) OU < OT
c) OU = ½ OT
d) OU = OT
View Answer
Explanation: Since PQRS is a parallelogram,
PQ = RS (Opposite sides of a parallelogram)
⇒ ½ PQ = ½ RS
⇒ TQ = US ———- (i)
In ΔSOU and ΔQOT,
∠SUO = ∠QTO (Alternate interior angles)
SU = TQ (from equation i)
∠TOQ = ∠SOU (Vertically Opposite angles)
⇒ ΔSOU ≅ ΔQOT (ASA congruence criteria)
⇒ OU = OT (Corresponding parts of congruent triangles)
7. Find the value of ∠R and ∠S if ∠P : ∠Q = 1 : 4.
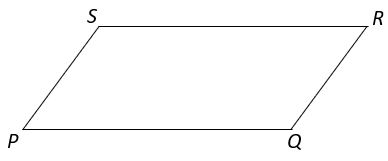
a) 45°, 90°
b) 36°, 144°
c) 144°, 36°
d) 50°, 40°
View Answer
Explanation: Since PQRS is a parallelogram, opposite angles are equal.
⇒ ∠P = ∠R and ∠Q = ∠S
Also, ∠P : ∠Q = 1 : 4
⇒ ∠P = ∠R = k and ∠Q = ∠S = 4k
Now, ∠P + ∠Q + ∠R + ∠S = 360° (Angle sum property of quadrilateral)
⇒ k + 4k + k + 4k = 360°
⇒ 10k = 360°
⇒ k = 36°
Hence, ∠R = k = 36° and ∠S = 4k = 144°.
8. From the figure find the length of AD is perimeter of parallelogram ABCD is 26cm.
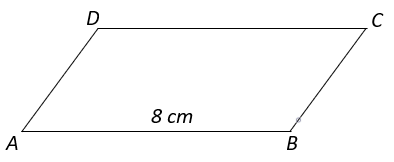
a) 10 cm
b) 15 cm
c) 12 cm
d) 5 cm
View Answer
Explanation: Since ABCD is a parallelogram, opposite sides are equal.
⇒ AB = CD = 8cm and AD = BC ————– (i)
Now, perimeter of ABCD = 26cm
⇒ AB + BC + CD + DA = 26cm
⇒ 2 x 8 + 2AD = 26cm (from equation i)
⇒ 2AD = 10cm
⇒ AD = 5 cm.
9. Find the ∠POQ if PQRS is a parallelogram and PO and OQ are angle bisectors.
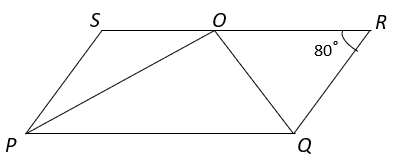
a) 30°
b) 45°
c) 90°
d) 180°
View Answer
Explanation: Since PQRS is a parallelogram, opposite sides angles are equal.
⇒ ∠P = ∠R = 80° and ∠Q = ∠S ————– (i)
Now, ∠P + ∠Q + ∠R + ∠S = 360° (Angle sum property of quadrilateral)
⇒ 80° + 2∠Q + 80° = 360° (from equation i)
⇒ ∠Q = 100°
Now, In ΔPOQ, ∠QPO = ½ ∠P = 40°
And ∠OQP = ½ ∠Q = 50°
∠QPO + ∠OQP + ∠POQ = 180° (Angle sum property of triangle)
⇒ 40° + 50° + ∠POQ = 180°
⇒ ∠POQ = 90°.
Sanfoundry Global Education & Learning Series – Mathematics – Class 9.
To practice all areas of Mathematics, here is complete set of 1000+ Multiple Choice Questions and Answers.
- Practice Class 8 Mathematics MCQs
- Practice Class 10 Mathematics MCQs
- Buy Class 9 - Mathematics Books
