This set of Class 9 Maths Chapter 13 Multiple Choice Questions & Answers (MCQs) focuses on “Surface Area of a Sphere”.
1. Surface area of a sphere of radius “r” is given by __________
a) 2πr2
b) 4πr2
c) 3πr2
d) πr2
View Answer
Explanation: If a sphere has radius equal to ”r”, then its surface area is given by 4πr2.
2. Curved surface area of hemisphere of radius “r” is equal to __________
a) 2πr2
b) 4πr2
c) 3πr2
d) πr2
View Answer
Explanation: Hemisphere is created when a sphere is divided in two equal parts.
Hence, the curved surface are of a hemisphere = \(\frac{Surface \,area \,of \,a \,sphere}{2}\)
= \(\frac{4πr^2}{2}\)
= 2πr2.
3. Total surface are of a hemisphere of radius “r” is equal to __________
a) 2πr2
b) 4πr2
c) 3πr2
d) πr2
View Answer
Explanation: Total surface area of a hemisphere = Curved surface area + Base area
= 2πr2 + πr2
= 3πr2.
4. Total surface area of a hemisphere is 4158cm2, the diameter of the hemisphere is equal to __________ cm. (Take π = \(\frac{22}{7}\))
a) 40
b) 20
c) 21
d) 42
View Answer
Explanation: We know that total surface area of a hemisphere = 3πr2
3πr2= 4158
3 * \(\frac{22}{7}\) * r2 = 4158
r2 = 441
Hence, r = 21cm
Therefore, diameter of hemisphere = 2r = 2 * 21 = 42cm.
5. If surface area of a sphere of radius “R” is equal to curved surface area of a hemisphere of radius “r”, what is the ratio of R/r?
a) 1/2
b) 1/√2
c) 2
d) √2
View Answer
Explanation: We know that surface area of a sphere of radius “R” is given by 4πR2 and
curved surface area of hemisphere of radius “r” is equal to 2πr2.
It is given that surface area of a sphere of radius “R” is equal to curved surface area of a hemisphere of radius “r”.
Hence, 4πR2 = 2πr2
2R2 = r2
\(\frac{R^2}{r^2} = \frac{1}{2}\)
\(\frac{R}{r} = \frac{1}{\sqrt{2}}\).
6. A sphere of radius “r” is fitted in a cylinder of height “h” such that the top of the sphere reaches only half the height of cylinder as shown in the figure. What is the ratio of curved surface area of a cylinder to surface area of a sphere?
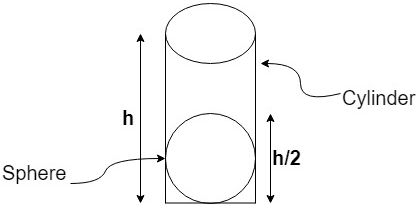
a) \(\sqrt{2}\):1
b) 4:1
c) 2:1
d) 1:2
View Answer
Explanation: It can be seen that h = 4r … (1)
We know that curved surface area of a cylinder = 2πrh
And surface area of a sphere = 4πr2
(We know that curved surface area of a cylinder)/(And surface area of a sphere) = 2πrh/(4πr2)
= \(\frac{2πr(4r)}{4πr^2}\) (From result (1))
= \(\frac{2πrh}{4πr^2}\)
= 2/1.
7. A hemispheric dome of radius 3.5m is to be painted at a rate of ₹600/m2. What is the cost of painting it? (Take π = \(\frac{22}{7}\))
a) ₹46200
b) ₹45000
c) ₹47260
d) ₹48375
View Answer
Explanation: We know that curved surface are of a hemisphere = 2πr2
= 2 * \(\frac{22}{7}\) * (3.5)2
= 77m2
Now, the cost of painting 1m2 of area = ₹600
Then, the cost of painting 77m2 of area = 77 * 600
= ₹46200.
8. A balloon’s radius increases 3 times when the air is pumped in it. If the surface area of the balloon after pumping the air is A2 and its surface area before pumping the air is A1, then what is the value of \(\frac{A_1}{A_2}\) ?
a) \(\frac{9}{1}\)
b) \(\frac{1}{3}\)
c) \(\frac{3}{1}\)
d) \(\frac{1}{9}\)
View Answer
Explanation: Let the radius of the balloon before pumping the air be “r”, then
A1 = 4πr2
The radius of the balloon after pumping the air = 3r (given)
Hence, A2 = 4π(3r)2
Therefore, \(\frac{A_1}{A_2} = \frac{4πr^2}{4π(3r)^2} = \frac{1}{9}\).
Sanfoundry Global Education & Learning Series – Mathematics – Class 9.
To practice all chapters and topics of class 9 Mathematics, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
- Practice Class 8 Mathematics MCQs
- Practice Class 10 Mathematics MCQs
- Check Class 9 - Mathematics Books
