Class 9 Maths MCQ – Circles – Perpendicular from the Centre to a Chord

This set of Class 9 Maths Chapter 10 Multiple Choice Questions & Answers (MCQs) focuses on “Circles – Perpendicular from the Centre to a Chord”.

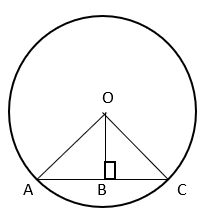
1. What is the value of AC if radius of circle is 5cm and OB = 3cm?

a) 5cm
b) 8cm
c) 4cm
d) 2cm
View Answer

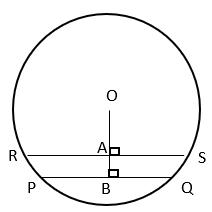
2. Find the value of AB if radius of circle is 10cm and PQ = 12cm and RS = 16cm?

a) 14cm
b) 16cm
c) 4cm
d) 2cm
View Answer

Answer: d
Explanation:

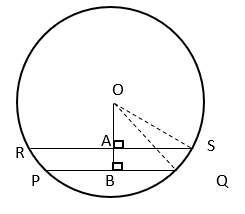
Since radius of circle = 10cm, OS = OQ = 10cm
In ΔBOQ, ∠OBQ = 90°
and BQ = PQ/2 = 6cm  (perpendicular from centre to a chord bisects the chord)
By Pythagoras theorem, OQ² = OB² + BQ²
⇒ 10² = 6² + OB²
⇒ OB² = 100 – 36 = 64
⇒ OB = 8cm
Similarly, In ΔAOS, ∠OAS = 90°
and AS = RS/2 = 8cm  (perpendicular from centre to a chord bisects the chord)
By Pythagoras theorem, OS² = OA² + AS²
⇒ 10² = 8² + OA²
⇒ OA² = 100 – 64 = 36
⇒ OA = 6cm
Now, AB = OB – OA
⇒ AB = 8 – 6 = 2cm.

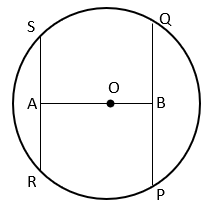
3. Find the radius of circle if AB = 7cm, RS = 6cm and PQ = 8cm.

a) 5cm
b) 8cm
c) 4cm
d) 20cm
View Answer

Answer: a
Explanation:

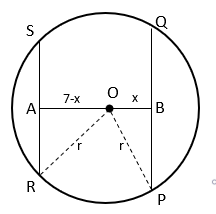
Let r be the radius of circle.
Since perpendicular from centre to a chord bisects the chord,
AR = RS/2 = 3cm and BP = PQ/2 = 4cm
In ΔBOP, ∠OBP = 90°
By Pythagoras theorem, OP² = OB² + BP²
⇒ r² = x² + (4)²
⇒ r² = x² + 16  ——————- (i)
Similarly, In ΔAOR, ∠OAR = 90°
By Pythagoras theorem, OR² = OA² + AR²
⇒ r² = (7 – x)² + (3)²
⇒ r² = (7 – x)² + 9  ———————— (ii)
From equation i and ii, x² + 16 = (7 – x)² + 9
⇒ x² + 16 = 7² – 2 x 7 x x + x² + 9
⇒ 2 x 7 x x = 49 – 16 + 9
⇒ x = 3
Substituting value of x in equation i, r² = 3² + 16
⇒ r = 5cm.

4. What is the ratio of PQ/RS if OT is perpendicular to line l?

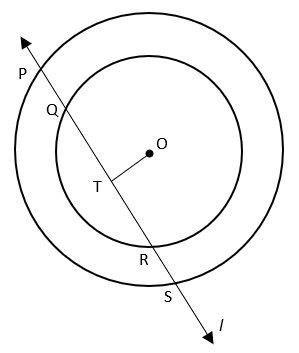
a) 0.5
b) 2
c) 1
d) 1.5
View Answer

5. What is the length of AD if distance between centres of the two circles is 9cm?

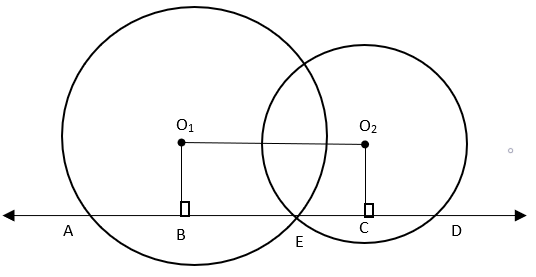
a) 9cm
b) 20cm
c) 15cm
d) 18cm
View Answer

6. Two circles of radius 13cm and 17cm intersect at A and B. What is the distance between the centres of the circles if AB = 24cm?

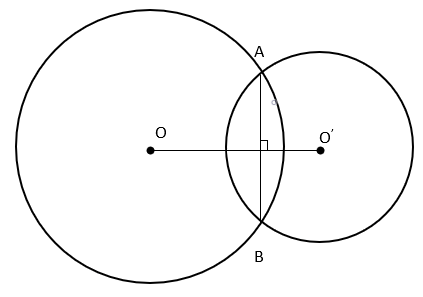
a) 15cm
b) 25cm
c) 22cm
d) 14cm
View Answer

Answer: d
Explanation:

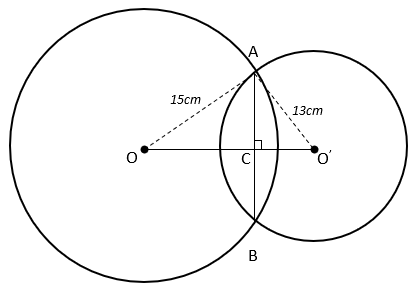
Since line joining the centres of the circles bisects the common chord, AC = BC = 12cm.
Also, In ΔAOC, ∠OCA = 90°
By Pythagoras theorem, OA² = OC² + AC²
⇒ 15² = OC² + 12²
⇒ OC² = 225 – 144
⇒ OC = 9cm
Similarly, In ΔAO’C, ∠O’CA = 90°
By Pythagoras theorem, O’A² = O’C² + AC²
⇒ 13² = O’C² + 12²
⇒ OC² = 169 – 144
⇒ OC = 5cm
Now, OO’ = OC + O’C
⇒ OO’ = 9 + 5 = 14cm.

7. What is the value of ∠PSQ in the given figure?

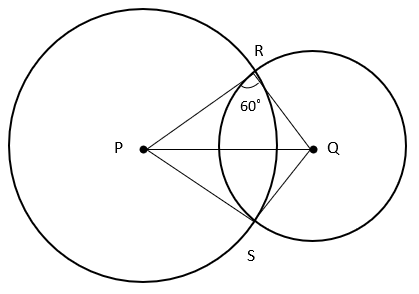
a) 90°
b) 60°
c) 30°
d) 45°
View Answer

Sanfoundry Global Education & Learning Series – Mathematics – Class 9.

To practice all chapters and topics of class 9 Mathematics, here is complete set of 1000+ Multiple Choice Questions and Answers.

If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]