This set of Class 9 Maths Chapter 7 Multiple Choice Questions & Answers (MCQs) focuses on “Congruence of Triangle – 2”.
1. What is the length of TS if PT = 6 cm and PQ || RS and T is the midpoint of QR?
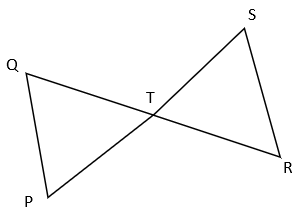
a) 5 cm
b) 6 cm
c) 8 cm
d) 4 cm
View Answer
Explanation: From figure, In ΔPQT and ΔSRT,
∠PQT = ∠TRS (Alternate Interior angles as PQ || RS)
QT = TR (T is the midpoint of QR)
∠PTQ = ∠RTS (vertically Opposite angles)
⇒ ΔPQT ≅ ΔSRT (ASA congruence criterion)
⇒ TS = PT = 6 cm. (Corresponding parts of congruent triangles).
2. What is the value of ∠PQB if PQ ⊥ PB and RS ⊥ AR and RS = PQ, AP = BR?
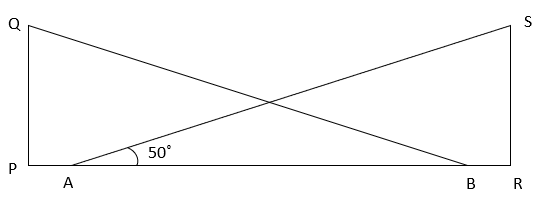
a) 50°
b) 40°
c) 80°
d) 100°
View Answer
Explanation: From figure, In ΔARS, ∠ARS + ∠SAR + ∠SRA = 180° (Angle sum property of triangle)
⇒ 90° + 50° + ∠RSA = 180° (RS ⊥ AR, ∠SRA = 90°)
⇒ ∠RSA = 40° ————– (i)
Also, AP = BR
⇒ AP + AB = BR + AB
⇒ PB = AR —————– (ii)
In ΔARS and ΔPQB, RS = PQ (given)
∠QPB = ∠SRA = 90°
PB = AR (from ii)
⇒ ΔARS ≅ ΔBQP (SAS congruence criterion)
⇒ ∠PQB = ∠RSA = 40° (Corresponding parts of congruent triangles)
3. Find the value of ∠ABD if AB = AC and DB = DC.
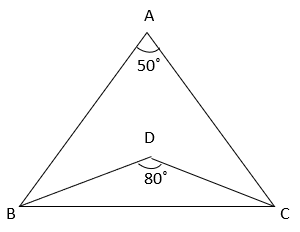
a) 20°
b) 45°
c) 30°
d) 15°
View Answer
Explanation: From figure, in ΔDBC, DB = DC ⇒ ∠DBC = ∠DCB (Angles opposite to equal sides are equal)
Also, ∠DBC + ∠DCB + ∠BDC = 180° (Angle sum property of triangle)
⇒ 80° + 2∠DBC = 180°
⇒ ∠DBC = 50° ————– (i)
In ΔABC, AB = AC ⇒ ∠ABC = ∠ACB (Angles opposite to equal sides are equal)
Also, ∠ABC + ∠ACB + ∠BAC = 180° (Angle sum property of triangle)
⇒ 50° + 2∠ABC = 180°
⇒ ∠ABC = 65° ————– (i)
Now, ∠ABD = ∠ABC – ∠DBC = 65° – 50° = 15°.
4. Which of the following relation is correct if the altitudes BD and CE are equal?
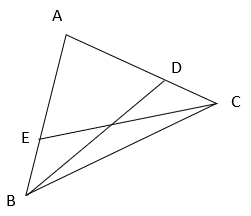
a) AB = AC
b) AB > AC
c) AB < AC
d) AB = ½ AC
View Answer
Explanation: From figure, In ΔABD and ΔACE,
∠ADB = ∠AEC = 90° (BD and CE are altitudes)
BD = CE (given)
∠BAD = ∠CAE (common angle)
⇒ ΔABD ≅ ΔACE (ASA congruence criterion)
⇒ AB = AC (Corresponding parts of congruent triangles).
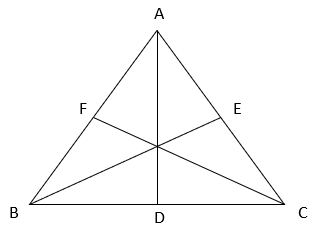
5. Identify the type of triangle if altitudes AD, BE and CF are equal.
a) Right angled triangle
b) Obtuse triangle
c) Equilateral triangle
d) Scalene triangle
View Answer
Explanation: From figure, in ΔBEC and ΔBFC,
BC = BC (Common)
BE = CF (given)
∠BEC = ∠BFC = 90°
⇒ ΔBEC ≅ ΔBFC (RHS congruence criterion)
⇒ ∠EBC = ∠FCB (Corresponding parts of congruent triangles)
⇒ AB = AC ———-(i) (Sides opposite to equal angles are equal)
Similarly, ΔABD ≅ ΔABE by RHS congruence criterion
⇒ ∠DBA = ∠DAB (Corresponding parts of congruent triangles)
⇒ AB = BC ———-(ii) (Sides opposite to equal angles are equal)
From equation i and ii, AB = BC = AC ⇒ ABC is an equilateral triangle.
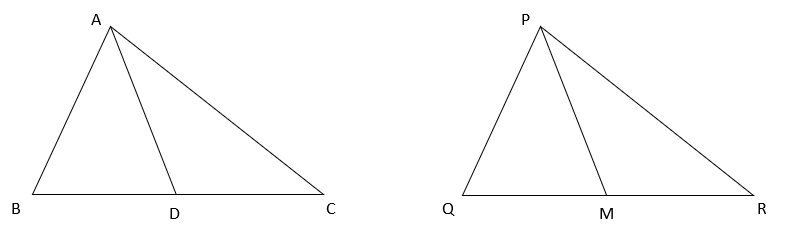
6. Which of the following option is correct if AD and PM are medians and are equal and AB = PQ and BC = QR?
a) ΔABD ≅ ΔPQM
b) ΔABD ≅ ΔPQC
c) ΔABC ≅ ΔPQM
d) ΔABD ≅ ΔPMR
View Answer
Explanation: From figure, BC = QR
⇒ ½ BC = ½ QR
⇒ BD = QM ————— (i)
In ΔABD and ΔPQM,
AB = PQ (given)
BD = QM (from i)
AD = PM (given)
⇒ ΔABD ≅ ΔPQM (SSS congruence criterion).
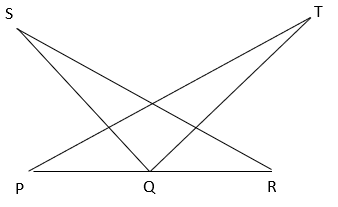
7. Which of the following option is correct if ∠PQS = ∠TQR, ∠SRP = ∠TPR and PQ = QR?
a) QS = QT
b) QS = 2QT
c) PT = 2RS
d) PT = ½ RS
View Answer
Explanation: From figure, ∠PQS = ∠TQR
⇒ ∠PQS + ∠SQT = ∠TQR + ∠SQT
⇒ ∠PQT = ∠SQR ————— (i)
In ΔPQT and ΔSQR,
∠TPQ = ∠SRQ (given)
PQ = QR (given)
∠PQT = ∠SQR (from equation i)
⇒ ΔPQT ≅ ΔSQR (ASA congruence criterion)
⇒ QT = QS and PT = RS (Corresponding parts of congruent triangles).
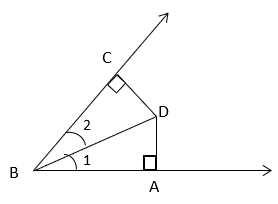
8. What is the relation between ∠1 and ∠2 if AD = CD?
a) ∠1 > ∠2
b) ∠1 < ∠2
c) ∠1 = ∠2
d) ∠1 = ½ ∠2
View Answer
Explanation: From figure, in ΔABD and ΔBCD,
∠BAD = ∠BCD = 90°
AQ = CD (given)
BD = BD (common side)
⇒ ΔABD ≅ ΔCBD (RHS congruence criterion)
⇒ ∠1 = ∠2 (Corresponding parts of congruent triangles).
Sanfoundry Global Education & Learning Series – Mathematics – Class 9.
To practice all chapters and topics of class 9 Mathematics, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
- Check Class 9 - Mathematics Books
- Practice Class 8 Mathematics MCQs
- Practice Class 10 Mathematics MCQs
