This set of Class 9 Maths Chapter 13 Multiple Choice Questions & Answers (MCQs) focuses on “Surface Area of a Right Circular Cone”.
1. In the figure given below, the cone is right circular cone.
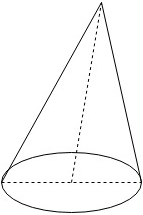
a) True
b) False
View Answer
Explanation: For the cone to be right circular cone, the line joining its vertex to the centre of its base have to be perpendicular to the base. (As shown in the below figure)
But we can see in the given figure that the line is not perpendicular to the base, hence the given cone is not right circular cone.
2. The total surface area of a cone of base radius “r” and slanted height “l” is equal to __________
a) πrl + 2πr2
b) 2πrl + 2πr2
c) πrl + πr2
d) 2πr2
View Answer
Explanation: Total surface area of a cone of base radius “r” and slanted height “l”
= Curved surface area of a cone + Base area of a cone
= πrl + πr2.
3. What is the total surface area of a cone of radius 7cm and height 24cm? (Take π = \(\frac{22}{7}\))
a) 710 cm2
b) 704 cm2
c) 700 cm2
d) 725 cm2
View Answer
Explanation: Given, r = 7cm and h = 24cm
From the figure,
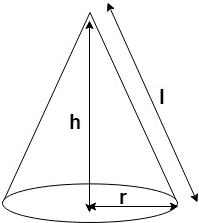
We can say that according to the Pythagoras theorem, l2 = r2 + h2
= 72 + 242
= 625
Therefore, l = 25cm
We know that total surface area of a cone = πrl + πr2
= πr (l + r)
= \(\frac{22}{7}\) * 7 (25+7)
= 704 cm2.
4. The curved surface area of a cone is 1980 cm2 and its radius is 21cm, what is the slanted height of a cone? (Take π = \(\frac{22}{7}\))
a) 25cm
b) 28cm
c) 35cm
d) 30cm
View Answer
Explanation: We know that the curved surface area of a cone = πrl
πrl = 1980
\(\frac{22}{7}\) * 21 * l = 1980
l = 30cm.
5. A tent of conical shape of base radius 28m and slanted height 20m is to be made from a certain material. What is the total cost of clothing material if the rate of material is ₹80/m2? (Take π = \(\frac{22}{7}\))
a) ₹140800
b) ₹150000
c) ₹130500
d) ₹140000
View Answer
Explanation: The curved surface are of a conical tent = πrl
= \(\frac{22}{7}\) * 28 * 20
= 1760m2
Cost of 1m2 of material = ₹80
Hence, the total cost of 1760m2 = 1760 * 80
= ₹140800.
6. A vessel of conical shape of radius 14cm and slanted height 20cm is to be coloured. What is the cost of painting at a rate of ₹2/cm2? (Take π = \(\frac{22}{7}\))
a) ₹1540
b) ₹1660
c) ₹1760
d) ₹1500
View Answer
Explanation: We know that curved surface area of We know that the curved surface area of a cone = πrl
For the given conical vessel, r = 14cm and l = 20cm (given)
Hence, curved surface area of vessel = πrl
= \(\frac{22}{7}\) * 14 * 20
= 880cm2
Now, the cost of painting 1cm2 area = ₹2
Then the cost of painting 880cm2 area = 880*2
= ₹1760.
Sanfoundry Global Education & Learning Series – Mathematics – Class 9.
To practice all chapters and topics of class 9 Mathematics, here is complete set of 1000+ Multiple Choice Questions and Answers.
- Check Class 9 - Mathematics Books
- Practice Class 8 Mathematics MCQs
- Practice Class 10 Mathematics MCQs
