This set of Class 9 Maths Chapter 7 Multiple Choice Questions & Answers (MCQs) focuses on “Inequalities in a Triangles”.
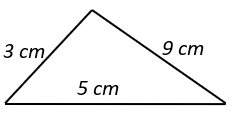
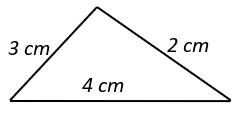
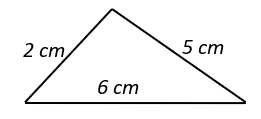
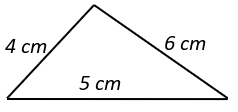
1. Which of the following figures does not represent a triangle?
a)
b)
c)
d)
View Answer
Explanation: Sum of any two sides of a triangle should be greater than the third side.
So, triangle with sides 3cm, 5cm, 9cm does not satisfy the condition. (3 + 5 = 8 < 9).
2. Which among the following statements are not correct?
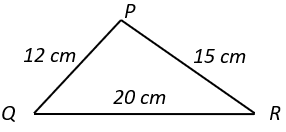
a) ∠P is the largest angle
b) ∠R is the smallest angle
c) ∠P is the smallest angle
d) ∠P > ∠Q
View Answer
Explanation: In a triangle, angle opposite to the longest side is largest and angle opposite to the shortest side is the smallest. So, in triangle PQR, QR is the longest side. Hence ∠P is the largest angle. Similarly, QP is the shortest side. Hence ∠R is the smallest angle. Therefore, ∠P > ∠Q > ∠R.
3. Identify the correct relation if x > y.
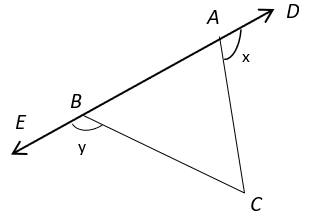
a) AB < AC
b) AB > AC
c) AB < 2AC
d) AB = AC
View Answer
Explanation: Given that, x > y.
From Figure, ∠EBC + ∠CBA = 180° (Linear Pair)
And ∠CAD + ∠CAB = 180° (Linear Pair)
So, ∠EBC + ∠CBA = ∠CAD + ∠CAB
⇒ x + ∠CBA = y + ∠CAB
The above condition is valid only when ∠CBA < ∠CAB as x > y.
So, ∠CBA < ∠CAB
⇒ AC < AB (side opposite to larger angle is the longer side).
4. Identify the correct relation if x : y : z = 1 : 3 : 5.
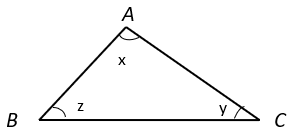
a) BC > AB > AC
b) AC < BC < AB
c) BC > AC > AB
d) BC < AC < AB
View Answer
Explanation: x : y : z = 1 : 3 : 5
In ΔABC, ∠A + ∠B + ∠C = 180° (Angle sum property of triangle)
⇒ x + y + z = 180°
⇒ k + 3k + 5k = 180°
⇒ k = 20°
∠A = k = 20°, ∠B = 3k = 60°, ∠C = 5k = 100°
Hence, ∠A < ∠B < ∠C
So, BC < AC < AB as the side opposite to the largest angle is the longest and side opposite to smallest angle is the shortest.
5. Which among the following relation is correct if AD = AC?
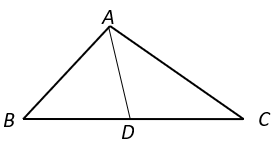
a) AB < AD
b) AB > AD
c) AB = AD
d) AB = ½ AD
View Answer
Explanation: In ΔACD, AD = AC
⇒ ∠ADC = ∠ACD ————–(i) (Angles opposite to equal sides are equal)
⇒ ∠ADC = ∠ACB ————–(ii)
Since, exterior angle of a triangle is greater than each of the interior opposite angle,
∠ADC > ∠ABD
⇒ ∠ACB > ∠ABC (From equation ii)
⇒ AB > AC (Side opposite to larger angle is the longer side in a triangle)
⇒ AB > AC (AD = AC).
6. Which among the following is the shortest?
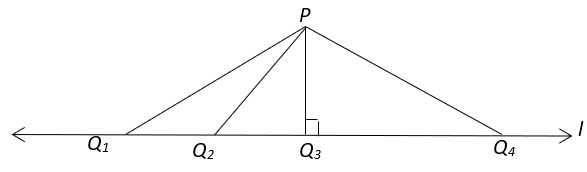
a) PQ3
b) PQ1
c) PQ4
d) PQ2
View Answer
Explanation: Among all the segments that can be drawn to a given line from a given point (not on the line), the perpendicular line segment is the shortest. Hence, PQ3 which is perpendicular to line l is the shortest line segment.
7. Which among the following relation holds true if AD, BE and DF are the altitudes of the triangle?
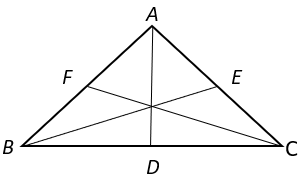
a) AD + BE + CF > AB + BC + AC
b) AD + BE + CF = AB + BC + AC
c) AD + BE + CF < AB + BC + AC
d) AD + BE + CF > 2(AB + BC + AC)
View Answer
Explanation: Among all the segments that can be drawn to a given line from a given point (not on the line), the perpendicular line segment is the shortest.
So, In ΔABC, AD ⊥ BC ⇒ AB > AD and AC > AD
⇒ AB + AC > 2AD ———–(i)
BE ⊥ AC ⇒ BC > BE and BA > BE
⇒ BC + BA > 2BE ———–(ii)
CF ⊥ AB ⇒ CA > CF and CB > CF
⇒ CA + CB > 2CF ———–(iii)
Adding equation i, ii and iii, AB + AC + BC + BA + CA + CB > 2AD + 2BE + 2CF
⇒ 2(AB + BC + AC) > 2(AD + BE + CF)
⇒ (AB + BC + AC) > (AD + BE + CF).
8. Find the correct relation among the following.
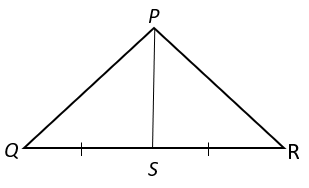
a) PQ + PR > 2PS
b) PQ + PR < 2PS
c) PQ + PR < PS
d) PQ + PR = ½ PS
View Answer
Explanation: From Figure, QS = QR. So, PS is the median from P to side QR.
As sum of any two sides of a triangle is greater than twice the median drawn to the third side,
PQ + PR > 2PS.
9. Identify the correct relation among the following.
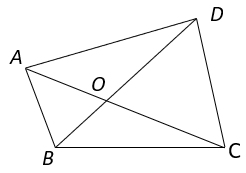
a) AB + BC + CD + AD = AC + BD
b) AB + BC + CD + AD > AC + BD
c) AB + BC + CD + AD < 2(AC + BD)
d) AB + BC + CD + AD = ¼ (AC + BD)
View Answer
Explanation: Since sum of any two sides of a triangle is greater than the third side,
In ΔABC, AB + BC > AC ———- (i)
In ΔACD, AD + CD > AC ———- (ii)
In ΔBCD, BC + CD > BD ———- (iii)
In ΔABD, AB + AD > BD ———- (iv)
Adding equation i, ii, iii and iv,
AB + BC + AD + CD + BC + CD + AB + AD > AC + AC + BD + BD
⇒ 2(AB + BC + CD + AD) > 2(AC + BD)
⇒ (AB + BC + CD + AD) > (AC + BD).
Sanfoundry Global Education & Learning Series – Mathematics – Class 9.
To practice all chapters and topics of class 9 Mathematics, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
- Check Class 9 - Mathematics Books
- Practice Class 8 Mathematics MCQs
- Practice Class 10 Mathematics MCQs
