This set of Class 9 Maths Chapter 13 Multiple Choice Questions & Answers (MCQs) focuses on “Surface Area of a Right Circular Cylinder”.
1. A transparent cylinder shown in the figure below is a right circular cylinder.
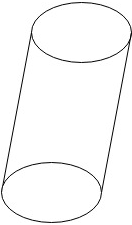
a) True
b) False
View Answer
Explanation: The cylinder shown in the figure is circular but it is not perpendicular to the base so we can’t say it is right circular cylinder.
A right circular cylinder is shown in the figure below. We can see that it is at the right angle to the base.
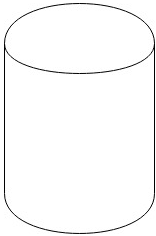
2. Curved surface area of a cylinder having base radius “r” and height “h” is equal to __________
a) 2πrh + 2πr2
b) 2πr2
c) 2πrh
d) 4πr2
View Answer
Explanation:
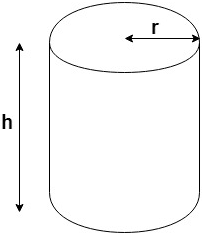
If we unfold the cylinder given in the above figure, the area of the rectangle gives us the area of curved surface area of a cylinder (As shown in the figure below).
One side of the rectangle is equal to “h” and the other side is equal to perimeter of circular edge of the cylinder, i.e. “2πr”.
Hence, the curved surface area of the cylinder = 2πr * h
= 2πrh.
3. Total surface area of a cylinder having base radius “r” and height “h” is equal to __________
a) 2πrh + 2πr2
b) 2πr2
c) 2πrh
d) 4πr2
View Answer
Explanation: Total surface area of a cylinder = curved surface area + 2 * area of the circular base
If we unfold the cylinder given in the above figure, the area of the rectangle gives us the area of curved surface area of a cylinder (As shown in the figure below).
One side of the rectangle is equal to “h” and the other side is equal to perimeter of circular edge of the cylinder, i.e. “2πr”.
Hence, the curved surface area of the cylinder = 2πr * h
= 2πrhArea of circular base = 2πr2
Hence, total surface area of a cylinder = curved surface area + 2 * area of the circular base
= 2πrh + 2πr2.
4. A cylinder has a curved surface area of 2640 cm2 and radius of 14 cm, what is the height of cylinder? (Take π = \(\frac{22}{7}\))
a) 16cm
b) 20cm
c) 28cm
d) 30cm
View Answer
Explanation: We know that curved surface area of a cylinder = 2πrh
Curved surface area = 2640 cm2 and r = 14 cm (given)
Therefore, 2 * \(\frac{22}{7}\) * 14 * h = 2640
h = 30cm.
5. A roller has diameter of 0.7m and length of 1m. It is used to roll over the cricket pitch. The surface area of the cricket pitch is equal to 60m2. How much revolution will roller make to move once over the pitch? (Take π = \(\frac{22}{7}\))
a) 25
b) 28
c) 30
d) 26
View Answer
Explanation: The effective area that will be in contact with the pitch is the curved surface area of the cylinder.
Diameter of the roller = 0.7m
Hence, radius of the roller = 0.35m and height (length here) of the roller = 1m
We know that curved surface area of a cylinder = 2πr
= 2 * \(\frac{22}{7}\) * 0.35 * 1
= 2.2 m2
Area of the cricket pitch = 60m2
Let’s assume that the roller makes “n” revolutions to move once over the pitch.
Therefore, n * curved surface area of the roller = surface area of the pitch
n = \(\frac{Surface \,area \,of \,the \,pitch}{Curved \,surface \,area \,of \,the \,roller}\)
= \(\frac{60}{2.2}\)
= 27.27
≈ 28 revolutions.
6. A cylindrical water container of radius 56 cm and height of 180 cm is to be made from metal. What is the area of metal required? (Take π = \(\frac{22}{7}\))
a) 28.9m2
b) 25.5m2
c) 30m2
d) 26.7m2
View Answer
Explanation: The area of material required will be equal to total surface area of the cylinder.
We know that the total surface area of the cylinder = 2πrh + 2πr2
= \((2 * \frac{22}{7} * 0.56 * 1.8) + {2 * \frac{22}{7} * (1.80)^2}\)
= 6.336 + 20.365
= 26.7 m2.
7. A water well has a height of 8m and diameter of 3.5m. What is the cost of plastering its curved surface and base at the rate of ₹50/m2? (Take π = \(\frac{22}{7}\))
a) ₹15000
b) ₹14500
c) ₹14000
d) ₹14700
View Answer
Explanation: The total area to be plastered = curved surface area + base area
= 2πrh + πr2
= \((2 * \frac{22}{7} * 1.75 * 8) + {\frac{22}{7}*(8)^2}\)
= 88 + 201.14
= 289.14 m2
≈ 290 m2
The cost of plastering area of 1 m2 = ₹50
Therefore, the cost of plastering area of 290 m2 = 290 * 50
= ₹14500.
Sanfoundry Global Education & Learning Series – Mathematics – Class 9.
To practice all chapters and topics of class 9 Mathematics, here is complete set of 1000+ Multiple Choice Questions and Answers.
- Check Class 9 - Mathematics Books
- Practice Class 8 Mathematics MCQs
- Practice Class 10 Mathematics MCQs
