Complex Numbers Roots Questions and Answers

This set of Complex Analysis Multiple Choice Questions & Answers (MCQs) focuses on “Roots of Complex Numbers.

1. The n^th roots of any number are in ____________
a) arithmetic progression
b) geometric progression
c) harmonic progression
d) no specific pattern
View Answer

Answer: b
Explanation: We know that re^iα=re^i(α+2π). Hence, if re^iα/n is a n^th root of a number, then, re^{i(α/n+2π/n)} is also a n^th root of that number. Hence, the roots are in G.P. with common ratio= e^i2π/n.

2. In the Argand Plane shown below, a,b,c,d are the 4-th roots of 16. Find the area of the closed Polygon having a,b,c,d as its vertices.

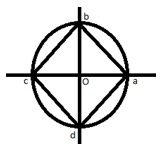
a) 2 sq. units
b) 4 sq. units
c) 8 sq. units
d) 16 sq. units
View Answer

Answer: c
Explanation: The complex numbers a,b,c,d are in G.P. with common ratio e^iπ/2. Therefore, a square is formed having side of 8^1/2(since O-a length is 2, therefore, b-a length is 8^1/2) . Hence the required area=(8^1/2)²=8 sq. units.

3. For k=1,2,…9, if we define z_k=cos(3kπ/10)+isin(2kπ/10), then is it true that for each z_k, there exists z_j satisfying z_k× z_j=1?
a) True
b) False
View Answer

Answer: a
Explanation: z_k= e^i(2kπ/10)⇒ z_k× z_j=e^{i(2π/10)(k+j)}, z_k is 10^th root of unity.
⇒\(\overline{z_k}\) is also 10^th root of unity. Taking z_j as \(\overline{z_k}\), we have z_k×z_j=1.

4. For k=1,2,…9, if we define z_k=cos(3kπ/10)+isin(2kπ/10), then is it possible that z₁×z=z_k has no Solution z?
a) True
b) False
View Answer

Answer: b
Explanation: z=z_k/z₁=e^{i(2kπ/10-2π/10)}=e^iπ/5(k-1)
For k = 2; z=e^iπ/5, therefore a solution always exists.

5. Find the value of the expression (-1/2+i√3/2)⁶³⁷+(-1/2-i√3/2)³³⁷.
a) -1
b) 0
c) 1
d) i
View Answer

Answer: a
Explanation: (-1/2+i√3/2)=ω and (-1/2-i√3/2)=ω², ω being the complex cube root of unity.
Therefore, expression has the value ω⁶³⁷+ω³³⁷=ω+ω²=-1.

Subscribe Now: Engineering Mathematics Newsletter | Important Subjects Newsletters

6. Let a and b be complex cube roots of unity. If x=7a+2b and y=2a+7b, then evaluate xy.
a) 9
b) 39
c) 45
d) 53
View Answer

Answer: d
Explanation: Write a=ω and b=ω².
Now, xy=(7a+2b)(2a+7b)=(7ω+2ω²)(2ω+7ω²)=14ω²+14ω+53=39 (since, 1+ω+ω²=0).

7. For integral x,y,z, find the range of |x+yω+zω²| if it is not true that x=y=z.
a) [1, ∞)
b) [√3, ∞)
c) (0, √3)
d) (0, ∞)
View Answer

Answer: a
Explanation: Put a=∞ and b=c=0 to show that maximum value tends to infinity.
Now, z=|x+yω+zω²|, hence, z²=|x+yω+zω²|²=(x²+y²+z²-xy-yz-zx)=1/2{(x-y)²+(y-z)²+(z-x)²}
Now if x=y, then y≠z and x≠z (given that x,y,z are not all equal)⇒(y-z)²≥1, also (z-x)²≥1 and
(x-y)²=0. Therefore, z²≥½(0+1+1)=1, hence |z|≥1.

8. Find the value of (1+ω)(1+ω²)(1+ω⁴)(1+ω⁸)…to 2n factors.
a) 1
b) 2
c) 3
d) 4
View Answer

Answer: a
Explanation: (1+ω)(1+ω²)(1+ω⁴)(1+ω⁸)…up to 2n factors
= (-ω²)(-ω)(1+ω)(1+ω²) …up to 2n factors
= 1×1×1×L up to n factors = 1.

9. If α,β,ȣ are the roots of equation x³–3x²+3x+7=0 and ω is cube root of unity, then evaluate
(α-1)/(β-1)+(β-1)/(ȣ-1)+(ȣ-1)/(α-1).
a) ω
b) ω²
c) 3ω
d) 3ω²
View Answer

Answer: d
Explanation: equation can be simplified to (x-1)³=-8⇒(x-1)/(-2)=(1)^1/3⇒roots: 1,ω,ω²
⇒ α=-1, β=1-2ω, ȣ=1-2ω². Therefore, required value=-2/(-2ω)+(-2ω)/(-2ω²)+(-2ω²)/(-2)
= 1/ω+1/ω+1/ω=3/ω=3ω².

10. Find the possible value(s) of Re(i^1/2)+|Im(i^1/2)|.
a) -1, 1
b) 0, √2
c) 0, 1
d) 1, √2
View Answer

Answer: b
Explanation: We can write: i=e^iπ/2⇒i^1/2=e^iπ/4=1/√2+i/√2, also i^1/2=e^i3π/4=-1/√2-i/√2
Hence, Re(i^1/2)+|Im(i^1/2)|=1/√2+1/√2=√2 OR -1/√2+1/√2=0.

11. Let ω and ω² be the non-real cube roots of unity and 1/(a+ω)+1/(b+ω)+1/(c+ω)=2ω² and 1/(a+ω²)+1/(b+ω²)+1/(c+ω²)=2ω, then calculate 1/(a+1)+1/(b+1)+1/(c+1).
a) 1
b) 2
c) 3
d) 4
View Answer

Answer: b
Explanation: Given relations can be written as: 1/(a+ω)+1/(b+ω)+1/(c+ω)=2/ω, and
1/(a+ω²)+1/(b+ω²)+1/(c+ω²)=2/ω²⇒ω and ω² are roots of 1/(a+x)+1/(b+x)+1/(c+x)=2/x.
⇒[3x²+2(a+b+c)x+bc+ca+ab]/[(a+x)(b+x)(c+x)]=2/x⇒x³+(bc+ca+ab)x-2abc=0.
Let 3^rd root be α (apart from ω and ω²). Then, α+ ω+ ω²=coefficient of x²=0⇒α=1. Hence, 1/(a+1)+1/(b+1)+1/(c+1)=2/1=2.

12. Find the cube root of 8i lying in the first quadrant of the complex plane.
a) i-√3
b) 2i+√3
c) i+2√3
d) i+√3
View Answer

Answer: d
Explanation: Let z³=8i⇒z³=-8i³⇒[z/(-2i)]³=1.
⇒z/(-2i)=1 or ω or ω²⇒z=-2i or -2iω or -2iω²
⇒z=-2i or i+√3 or i-√3 out of which i+√3 lies in the first quadrant.

13. If ω is the complex cube root of unity, then which among the following is a factor of the polynomial x⁶+ 4x⁵+3x⁴+2x³+x+1?
a) x+ω
b) x+ω²
c) (x+ω)(x+ω²)
d) (x–ω)(x–ω²)
View Answer

Answer: d
Explanation: Let f(x)=x⁶+ 4x⁵+3x⁴+2x³+x+1. Therefore, f(ω)= ω⁶+4ω⁵+3ω⁴+2ω³+ω+1=0
Since, ω² is the complex conjugate of ω, therefore ω² is also a root (roots occur in conjugate pairs). Therefore (x–ω)(x–ω²) is a root. Also, f(-ω)=(-ω)⁶+4(-ω)⁵+3(-ω)⁴+2(-ω)³+(-ω)+1=1-4ω²+3ω-2-ω+1≠0⇒-ω and hence -ω² are not the roots.

14. Find ∑_r=1(ar+b) ω^r-1 if ω is a complex nth root of unity.
a) n(n+1)a/2
b) nb/(1-n)
c) na/(ω-1)
d) n(n+1)a/(ω-1)
View Answer

Answer: c
Explanation: (a+b)+(2a+b)ω+(3a+b)ω²+…+(na+b)ω^n-1=b(1+ω+ω²+….+ω^n-1)+a(1+2ω+3ω²+…+nω^n-1)
Let S=1+2ω+3ω²+…+nω^n-1⇒Sω= ω+2ω²+…+(n-1)ω^n-1+nωⁿ⇒S(1-ω)=1+ω+ ω²+…+ω^n-1–nωⁿ=-n
⇒S=n/(ω-1)⇒E=na/(ω-1).

15. Which of the following is not equal to (-1)^1/3?
a) -1
b) (-√3+i)/(2i)
c) (√3+i)/(2i)
d) (√3–i)/(2i)
View Answer